16.1: Vectores

Última actualización
Guardar como PDF

Page ID: 84049

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Los vectores se utilizan en la mecánica de ingeniería para representar cantidades que tienen tanto una magnitud como una dirección. Muchas cantidades de ingeniería, como fuerzas, desplazamientos, velocidades y aceleraciones, necesitarán representarse como vectores para el análisis. Las cantidades vectoriales contrastan con valores escalares (como masa, área o velocidad), que tienen una magnitud pero ninguna dirección.

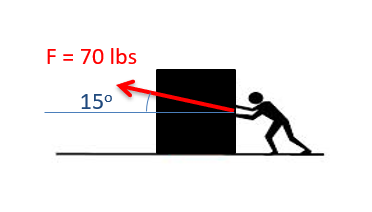
Una persona empuja un gran bloque hacia la izquierda, aplicando una fuerza de 70 lbs dirigida a 15° por encima de la horizontal. — Figura\(\PageIndex{1}\): La fuerza a continuación se representa como un vector. Tiene tanto una magnitud como una dirección.

Cuando se trata de vectores en ecuaciones, los ingenieros comúnmente denotan algo como un vector al poner una flecha sobre la variable. Las variables sin una flecha encima de ellas representan una cantidad escalar, o simplemente la magnitud de esa cantidad vectorial.

\ begin {align}\ text {Cantidad vectorial:}\ quad &\,\ vec {F}\\\ text {Cantidad escalar:}\ quad &\, F\ end {align}

En contraste con las cantidades escalares, no podemos sumarlas, restarlas, multiplicarlas o dividirlas simplemente sumando, restando, multiplicando o dividiendo las magnitudes. Las direcciones también jugarán un papel crítico en la resolución de ecuaciones que contienen cantidades vectoriales.

Representación vectorial:

Para representar una cantidad vectorial, generalmente tendremos dos opciones. Estas dos opciones son:

Forma de Magnitud y Dirección: Donde la magnitud se da como una sola cantidad y la dirección se da a través de un ángulo o combinación de ángulos.
Forma de componente: Donde la magnitud y dirección se dan a través de magnitudes de componente en cada dirección de coordenadas.

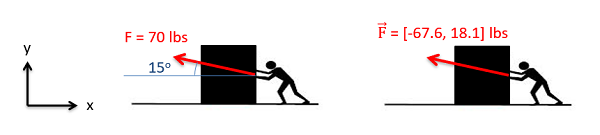
Dos diagramas de una misma situación, donde una persona empuja un bloque hacia la izquierda aplicando una fuerza dirigida tanto hacia la izquierda como hacia arriba. En un diagrama, ese vector de fuerza se representa con una magnitud de 70 lbs y una dirección de 15° por encima de la horizontal. En el segundo diagrama, ese mismo vector de fuerza se representa con componentes de -67.6 lbs en la dirección x hacia la izquierda o negativa y 18.1 lbs en la dirección y hacia arriba o positiva. — Figura\(\PageIndex{2}\): El dibujo anterior muestra una fuerza como vector. A la izquierda el vector se representa como una magnitud y una dirección. A la derecha se representa la misma fuerza en términos de sus\(x\) - y\(y\) -componentes.

La forma de magnitud y dirección de las cantidades vectoriales a menudo se utilizan al inicio y al final de un problema. Esto se debe a que a menudo es más fácil medir cosas como fuerzas y velocidades como magnitud y dirección al inicio de un problema, y muchas veces es más fácil visualizar el resultado final como una magnitud y dirección al final. Los vectores representados como una magnitud y dirección deben mostrarse visualmente mediante el uso de una flecha, donde la magnitud es la longitud de la flecha, y la dirección se muestra a través de la cabeza de la flecha y un ángulo o ángulos relativos a algunos ejes conocidos u otra dirección.

La forma componente de un vector se usa a menudo en medio del problema porque es mucho más fácil hacer matemáticas con cantidades vectoriales en forma de componente. Los vectores se pueden representar en forma de componentes de una de dos maneras. Primero podemos usar corchetes para indicar un vector, con los\(z\) componentes\(x\)\(y\),, y posiblemente separados por comas. Alternativamente, podemos escribir un vector en forma de componente usando las magnitudes delante de los vectores unitarios para indicar direcciones (generalmente los vectores\(\hat{i}\)\(\hat{j}\),, y\(\hat{k}\) unidades para las\(z\) direcciones\(x\)\(y\), y respectivamente). Ninguna de estas formas componentes se basa en una representación visual del vector como con la forma de magnitud y dirección, aunque es importante identificar claramente el sistema de coordenadas en diagramas anteriores.

\ begin {align}\ text {Con corchetes:}\ quad &\,\ vec {F} = [3,4,5]\\\ texto {Con vectores unitarios:}\ quad &\,\ vec {F} = 3\ hat {i} + 4\ hat {j} + 5\ hat {k}\ end {align}

Conversión entre representaciones vectoriales en 2D

Para nuestro análisis, a menudo nos resultará ventajoso tener los vectores en una forma u otra, y por lo tanto necesitaremos convertir el vector de una magnitud y dirección a forma de componente o viceversa. Para ello utilizaremos triángulos rectos y trigonometría.

Pasando de una magnitud y dirección a una forma de componente

Para pasar de una forma de magnitud y dirección a componente, primero dibujaremos un triángulo rectángulo con la hipotenusa siendo el vector original. El brazo horizontal del triángulo será entonces el\(x\) -componente del vector mientras que el brazo vertical es el\(y\) componente del vector. Si conocemos el ángulo del vector con respecto a la horizontal o la vertical, podemos usar la relación seno y coseno para encontrar los\(y\) componentes\(x\) y.

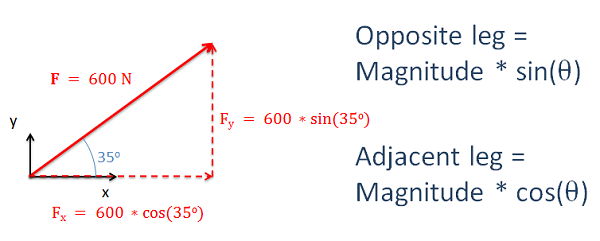
Un vector de fuerza con magnitud 600 N apunta hacia arriba y hacia la derecha, en un ángulo de 35° por encima de la horizontal. Una línea horizontal que apunta hacia la derecha se dibuja desde la cola del vector y se etiqueta como el componente del vector de fuerza original en la dirección x. Una línea vertical que apunta hacia arriba se dibuja desde esa línea horizontal hasta la cabeza del vector original, y se etiqueta como el componente del vector de fuerza original en la dirección y. Las magnitudes de estos componentes respectivos son F_x = 600 * cos (35°), y F_y = 600 * sin (35°). — Figura\(\PageIndex{3}\): Usando relaciones seno y coseno, podemos encontrar los\(y\) componentes\(x\) y de un vector.

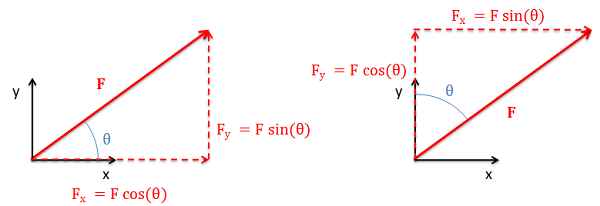
Es importante recordar que la forma en que medimos el ángulo afectará las relaciones seno y coseno. Multiplicar la magnitud por el seno siempre nos dará la pierna opuesta y multiplicar la magnitud por el coseno siempre nos dará la pierna adyacente.

Dos diagramas del mismo vector de fuerza F extendiéndose hacia arriba y hacia la derecha, con su cola en el origen de un plano de coordenadas cartesianas. En un diagrama, la dirección del vector es el ángulo theta que hace con el eje x positivo; por lo tanto, los componentes del vector se calculan como F_x = F cos (theta) y F_y = F sin (theta). En el otro diagrama, la dirección del vector es el ángulo theta que hace con el eje y positivo; por lo tanto, los componentes del vector se calculan como F_y = F cos (theta) y F_x = F sin (theta). — Figura\(\PageIndex{4}\): Dependiendo de cómo medimos el ángulo, el seno/coseno puede ser el componente\(x\) o el\(y\) componente. Recuerda que el seno siempre te dará la pierna opuesta, mientras que el coseno te dará la pierna adyacente.

Pasando de la forma del componente a la magnitud y dirección

Para encontrar la magnitud y la dirección de un vector usando componentes, utilizaremos el mismo proceso a la inversa. Dibujaremos los componentes como las patas de un triángulo rectángulo, donde la hipotenusa del triángulo muestra la magnitud y dirección del vector.

Para encontrar la magnitud del vector utilizaremos el Teorema de Pitágoras, tomando la raíz cuadrada de la suma de los cuadrados de cada componente. Para encontrar el ángulo, podemos usar fácilmente la función tangente inversa, relacionando las patas opuestas y adyacentes de nuestro triángulo rectángulo.

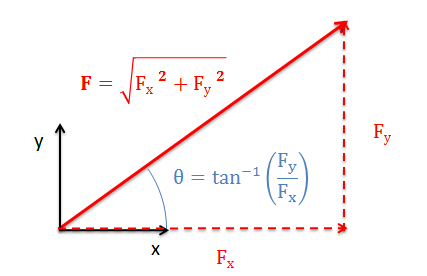
Gráfica de un vector F que se extiende hacia arriba y hacia la derecha, con su cola en el origen de un plano coordenado cartesiano. La magnitud de este vector se encuentra tomando la raíz cuadrada de la suma de los cuadrados de sus componentes, F_x y F_y, la dirección de este vector, en la forma del ángulo que forma con el eje x positivo, se encuentra dividiendo F_y por F_x, tomando luego la tangente inversa de este cociente. — Figura\(\PageIndex{5}\): Utilizaremos el Teorema de Pitágoras y la función tangente inversa para convertir el vector de nuevo en forma de magnitud y dirección.

Si conocemos la magnitud de la hipotenusa, también podemos usar las funciones sinusoidal inversa y coseno en lugar de la función tangente inversa para encontrar el ángulo. Al igual que con la conversión anterior, es importante identificar claramente la pata opuesta, la pata adyacente y la hipotenusa en nuestros diagramas y pensar en éstas al aplicar las funciones trigonométricas inversas.

Conversión entre representaciones vectoriales en 3D

En tres dimensiones, tendremos tres componentes (\(x\),\(y\), y\(z\)) para la forma de componente o una magnitud y dos ángulos para la dirección en magnitud y dirección forma. Para convertir entre formas necesitaremos dibujar en dos conjuntos de triángulos rectos. La hipotenusa del primer triángulo será el vector original y una de las patas será uno de los tres componentes. La otra pierna será entonces la hipotenusa del segundo triángulo. Las patas de este segundo triángulo serán entonces los dos componentes restantes como se muestra en el diagrama a continuación. Utilice relaciones de seno y coseno para encontrar la magnitud de cada componente en el camino. Este proceso general de dos triángulos rectos consecutivos siempre se mantendrá cierto, pero dependiendo de los ángulos que se den o elijan qué componentes terminan siendo qué pierna puede variar. Por esta razón, es importante trazar con cuidado todo en un diagrama.

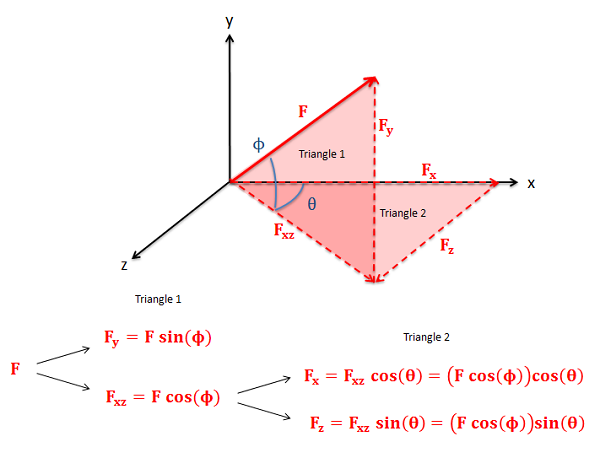
Un vector F, cuya cola está en el origen, en el primer octante de un sistema de coordenadas cartesianas tridimensionales con los ejes x e y en el plano de la pantalla y el eje z apuntando fuera de la pantalla. El vector F forma un ángulo de phi por encima del plano xz, formando la hipotenusa de un triángulo rectángulo cuyas patas son los componentes F_y y F_xZ del vector original. En el plano xz, el vector f_xZ forma un ángulo de theta con el eje x positivo, formando la hipotenusa de un triángulo rectángulo cuyas patas son los componentes F_x y F_z del vector original. — Figura\(\PageIndex{6}\): Para vectores 3D necesitaremos dibujar dos triángulos rectos para convertir entre formas.

Para pasar de la forma de componente de nuevo a una magnitud y dirección, utilizaremos la forma 3D del Teorema de Pitágoras (la magnitud será la raíz cuadrada de la suma de los tres componentes al cuadrado) y nuevamente podremos usar las funciones trigonométricas inversas para encontrar los ángulos. Simplemente necesitamos trabajar hacia atrás a través de los dos triángulos rectos en nuestro problema, así que nuevamente es importante dibujar cuidadosamente tus diagramas.

Método alternativo para encontrar componentes vectoriales 3D

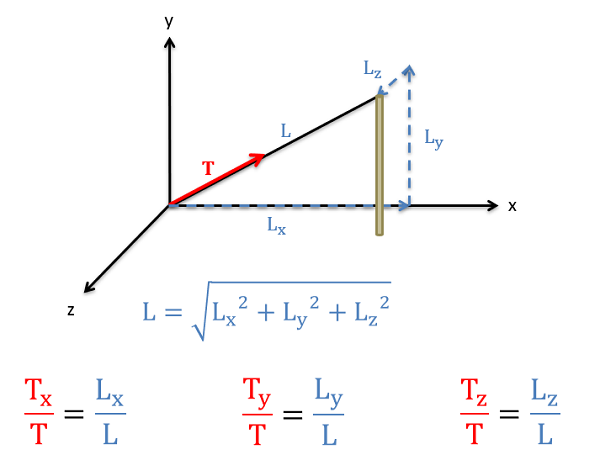
A veces, al igual que con la tensión en un cable, la geometría del cable se da en forma de componente en lugar de como ángulos. En casos como este podríamos usar la geometría para averiguar los ángulos y luego usar esos ángulos para averiguar los componentes, pero hay un atajo matemático que nos permitirá resolver para los componentes más rápidamente involucrando la relación de longitudes. Específicamente, las relaciones de los componentes de la longitud del cable a la longitud total del cable serán las mismas que la relación de los componentes de fuerza correspondientes a la magnitud general de la fuerza.

Para usar este método primero necesitaremos encontrar la longitud total del cable (u otra característica geométrica física) usando el Teorema de Pitágoras. Una vez que tenemos esa longitud total, encontramos una relación tomando el componente x de la longitud dividido por la longitud total. Para encontrar el\(x\) -componente de la fuerza, simplemente multiplicamos la magnitud general de la fuerza por esta relación de longitudes (\(L_x/L\)). El proceso para los\(z\) componentes\(y\) y sigue una trayectoria similar, excepto que las relaciones incluirían las longitudes\(y\) y de los\(z\) componentes en lugar del\(x\) componente.

El primer octante de un sistema de coordenadas cartesianas tridimensionales, con los ejes x e y en el plano de la pantalla y el eje z apuntando fuera de la pantalla. Un poste vertical, paralelo al eje y, tiene un extremo en el plano xz y el otro extremo conectado al origen a través de un cable tenso de longitud L. Una fuerza de tensión T apunta a lo largo de este cable, comenzando desde el origen. Debajo del diagrama, la relación entre los componentes de longitud del cable y los componentes de fuerza de tensión con sus respectivas cantidades totales se proporcionan como 3 relaciones separadas: T_x/T = L_x/L, T_y/T = L_y/L, y T_z/T = L_z/L. — Figura\(\PageIndex{7}\): El método alternativo de descomponer un vector en forma de componente se basa en las relaciones entre los componentes del cable y la longitud total del cable.

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/2RO7VZ_u0Iw.

Ejemplo\(\PageIndex{1}\)

Determinar los\(y\) componentes\(x\) y del vector que se muestra a continuación.

Un disco circular plano está acuñado en una ranura de lados rectos. Un lado de la ranura ejerce una fuerza con una magnitud de 300 N sobre el disco, dirigida hacia arriba y hacia la derecha a 40° por encima de la horizontal. — Figura\(\PageIndex{8}\): diagrama de problemas para Ejemplo\(\PageIndex{1}\). Una fuerza de magnitud 300 N se dirige hacia arriba y hacia la derecha, a 40° por encima de la horizontal.

Solución:: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/TRS6jiih96o.

Ejemplo\(\PageIndex{2}\)

Determinar los\(y\) componentes\(x\) y del vector que se muestra a continuación.

Un semáforo está suspendido de dos cables. Una fuerza de tensión T1 de magnitud 60 lbs actúa a lo largo de uno de estos cables, apuntando hacia arriba y hacia la derecha en un ángulo de 75° desde la vertical. — Figura\(\PageIndex{9}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\). Se ejerce una fuerza de tensión de magnitud 60 lbs a lo largo de un cable, dirigida hacia arriba y hacia la derecha en un ángulo de 75° desde la vertical.

Solución:: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/hUrlI6eLGvE.

Ejemplo\(\PageIndex{3}\)

El vector de velocidad del disco de hockey que se muestra a continuación se da en forma de componentes. Determinar la magnitud y dirección de la velocidad con respecto a los ejes dados.

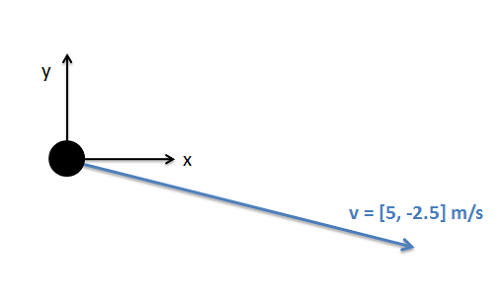
Un disco de hockey se localiza en el origen de un plano de coordenadas cartesianas de orientación estándar. Se experimenta un vector de velocidad apuntando hacia abajo y hacia la derecha, con un componente x de 5 m/s y un componente y de -2.5 m/s. — Figura\(\PageIndex{10}\): diagrama de problemas para Ejemplo\(\PageIndex{3}\). Un disco de hockey localizado en el origen de un plano de coordenadas cartesianas experimenta una velocidad de componentes\([5, -2.5]\) m/s.

Solución:: Video\(\PageIndex{4}\): Solución trabajada a problema de ejemplo\(\PageIndex{3}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/3GeIU3Fc_qA.

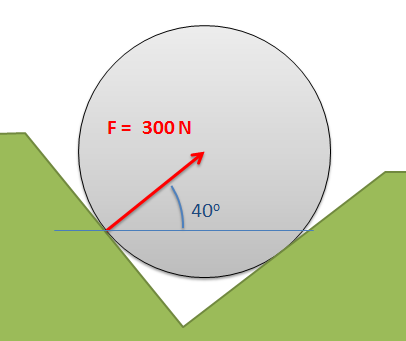
Ejemplo\(\PageIndex{4}\)

Determinar los\(x\),\(y\), y\(z\) componentes del vector de fuerza que se muestra a continuación.

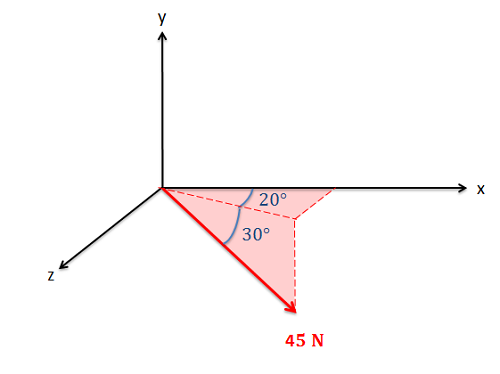
Un vector con su cola en el origen de un sistema de coordenadas cartesianas 3D, con los ejes x e y tendidos en el plano de la pantalla y el eje z apuntando fuera de la pantalla. El vector tiene una magnitud de 45 N. Su dirección es 20° fuera del plano de la pantalla hacia el espectador, y 30° por debajo del plano xz. — Figura\(\PageIndex{11}\): diagrama de problemas para Ejemplo\(\PageIndex{4}\). Un vector de fuerza de 45 Newton con su cola en el origen de un sistema de coordenadas cartesianas apunta 20° fuera de la pantalla hacia el espectador y 30° por debajo del plano de la horizontal.

Solución:: Video\(\PageIndex{5}\): Solución trabajada a problema de ejemplo\(\PageIndex{4}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/ZG31PoIfIEc.

Ejemplo\(\PageIndex{5}\)

Un cable como se muestra a continuación se usa para atar la parte superior de un poste a un punto en el suelo. El cable tiene una fuerza de tensión de 3 kN que actúa a lo largo de la dirección del cable como se muestra a continuación. ¿Cuáles son los\(z\) componentes\(x\)\(y\),, y de la fuerza de tensión que actúa sobre la parte superior del poste?

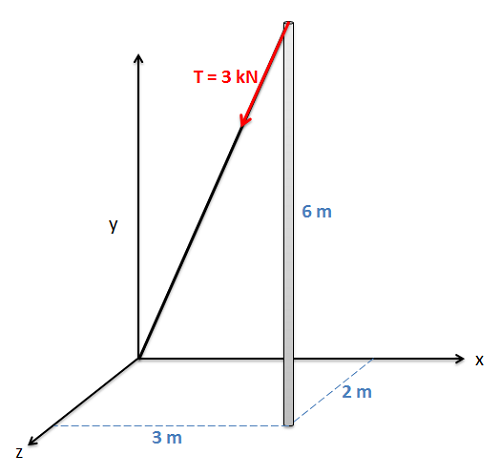
El primer octante de un sistema de coordenadas cartesianas tridimensional, con los ejes x e y dispuestos en el plano de la pantalla y el eje z apuntando fuera de la pantalla. Todos los ejes tienen unidades en metros. Un polo vertical de 6 metros de largo tiene un extremo ubicado en el punto (2, 0, 3) y se extiende hacia arriba desde ese punto paralelo al eje y. Un cable conecta el origen del sistema al extremo superior del polo, y una fuerza de tensión de 3 kN actúa a lo largo de ese cable, dirigida hacia el origen. — Figura\(\PageIndex{12}\): diagrama de problemas para Ejemplo\(\PageIndex{5}\). Un cable conecta el origen de un sistema de coordenadas cartesianas a la parte superior de un polo vertical de 6 metros de largo con su base en el punto (2, 0, 3) metros.

Solución:: Video\(\PageIndex{6}\): Solución trabajada a problema de ejemplo\(\PageIndex{5}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/dUJwBohfCTU.