17.3: Centroides en Volúmenes y Centro de Masa vía Integración

Última actualización
Guardar como PDF

Page ID: 84015

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

El centroide de un volumen puede considerarse como el centro geométrico de esa forma. A menudo se denota como\(C\), estando ubicado en las coordenadas\((\bar{x}, \bar{y}, \bar{z})\). Si este volumen representa una parte con una densidad uniforme (como la mayoría de las partes de un solo material) entonces el centroide también será el centro de masa, un punto generalmente etiquetado como\(G\).

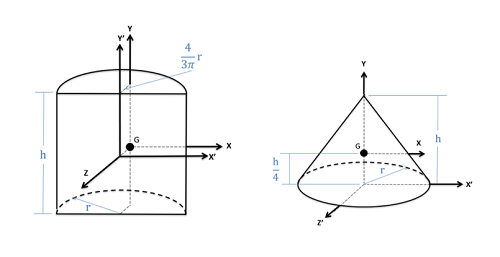
Un medio cilindro de altura h, extruido a partir de un semicírculo de radio r, tiene su centroide ubicado a lo largo de la línea de intersección de sus dos planos de simetría, 4r/ (3 pi) unidades alejadas del punto medio del borde recto del semicírculo. Un cono circular derecho de radio r y altura h, de pie sobre su base, tiene su centroide ubicado h/4 unidades por encima del punto medio de su base. — Figura\(\PageIndex{1}\): El punto centroide (\(C\)) o el centro de masa (\(G\)) para algunas formas comunes. (El centroide y el centro de masa son el mismo punto para cuerpos con una densidad uniforme)

Al igual que con los centroides de un área, los centroides de volúmenes y el centro de masa son útiles para una serie de situaciones en la secuencia del curso de mecánica, incluyendo el análisis de fuerzas distribuidas, simplificando el análisis de la gravedad (que es en sí misma una fuerza distribuida), y como paso intermedio en determinando momentos de inercia de masa.

Al igual que con las áreas, la ubicación del centroide (o centro de masa) para una variedad de formas comunes simplemente se puede buscar en tablas, como esta. Sin embargo, a menudo necesitaremos determinar el centroide o centro de masa para otras formas, y para ello generalmente usaremos uno de dos métodos.

Podemos usar la integral de primer momento para determinar la ubicación del centroide o centro de masa.
Podemos usar el método de piezas compuestas junto con tablas centroides para determinar la ubicación del centroide o centro de masa.

En esta página solo discutiremos el primer método, ya que el método de las piezas compuestas se discute en una sección posterior. Sin embargo, las tablas utilizadas en el método de piezas compuestas se derivan a través de la integral de primer momento, por lo que ambos métodos se basan en integrales de primer momento.

Encontrar el centroide de un volumen a través de la Integral del Primer Momento

Cuando encontremos el centroide de una forma tridimensional, estaremos buscando el\(x\),\(y\), y las\(z\) coordenadas (\(\bar{x}\),\(\bar{y}\), y\(\bar{z}\)) del punto que es el centroide de la forma.

Al igual que los cálculos centroides que hicimos con formas bidimensionales, estamos buscando encontrar la coordenada promedio de la forma en cada dimensión. Esto lo hacemos resumiendo todos los pedacitos de volumen por el\(x\),\(y\), o\(z\) coordenada de ese bit de volumen y luego dividiendo esa suma por el volumen total de la forma. Nuevamente utilizaremos el cálculo para resumir un número infinito de volúmenes infinitamente pequeños. Específicamente esta suma será el primer momento de volumen rectangular integral para la forma.

\[ C = G = (\bar{x}, \bar{y}, \bar{z}) \quad \text{for constant-density shapes} \nonumber\]

Trabajando en cada una de las tres direcciones de coordenadas terminamos con las siguientes tres ecuaciones.

\[\begin{align*} \bar{x} &= \dfrac{\displaystyle \int_V (dV * x)}{V} \\[4pt] \bar{y} &= \dfrac{\displaystyle \int_V (dV * y)}{V} \\[4pt] \bar{z} &= \dfrac{\displaystyle \int_V (dV * z)}{V} \end{align*}\]

Con estas nuevas ecuaciones tenemos la variable\(dV\) más que\(dA\), porque nos estamos integrando sobre un volumen más que sobre un área. Esto representa la tasa de cambio del volumen a medida que nos movemos a lo largo de un eje de un extremo a otro. La velocidad de cambio del volumen en cualquier punto de la forma será el área de la sección transversal que es perpendicular a ese eje multiplicada por la velocidad a la que nos movemos a lo largo de ese eje. Dado que el área de la sección transversal puede variar a medida que nos movemos a lo largo del eje, necesitaremos determinar una fórmula para el área de sección transversal en cualquier punto a lo largo de ese eje.

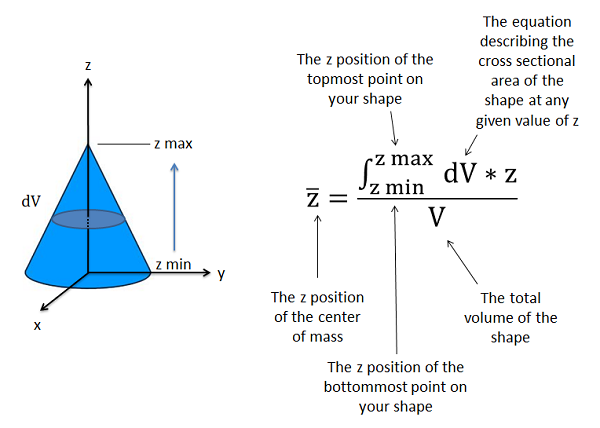
Un cono circular derecho se encuentra con su base en el plano XY, centrado en el origen, y su punta en algún punto en el eje z positivo. La coordenada z de la punta se etiqueta z_max, y el plano xy-( z=0) se etiqueta z_min. El cono se corta paralelo al plano XY en rodajas circulares delgadas, cada una con un volumen dV que iguala el área de la sección transversal por el pequeño cambio en z que representa la altura de la rebanada. La ecuación para la coordenada z del centroide del cono es la integral de dV veces z, evaluada de x_min a x_max, el conjunto dividido por el volumen total del cono. — Figura\(\PageIndex{2}\): La\(z\) coordenada del centroide/centro de masa.

Usando la integral de primer momento y las ecuaciones mostradas anteriormente, teóricamente podemos encontrar el centroide de cualquier volumen siempre y cuando podamos escribir una ecuación para describir el área de sección transversal para cada dirección. Para formas más complejas, sin embargo, determinar estas ecuaciones y luego integrar estas ecuaciones puede llegar a ser muy lento. Para estas formas complejas, lo más probable es que el método de piezas compuestas o herramientas informáticas sea mucho más rápido.

Uso de la simetría como acceso directo

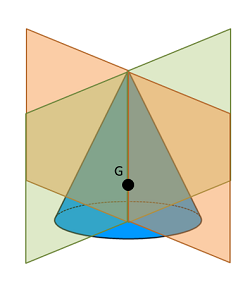
Al igual que con las áreas 2D, la simetría de forma puede proporcionar un atajo en muchos cálculos de centroides. Recuerde que la coordenada centroide es la media\(x\),\(y\), y\(z\) coordenada para todos los puntos de la forma. Si el volumen tiene un plano de simetría, eso significa que cada punto en un lado de la línea debe tener un punto equivalente en el otro lado de la línea. Esto significa que el valor promedio (también conocido como el centroide) debe estar dentro de ese plano. Si el volumen tiene más de un plano de simetría, entonces el centroide debe existir en la intersección de esos planos.

Un cono circular derecho tiene muchos planos de simetría, todos pasando a través de la línea que conecta la punta con el centro de la base circular. Por tanto, el centroide se encuentra en algún lugar a lo largo de esa línea. — Figura\(\PageIndex{3}\): Si un volumen tiene un plano de simetría, entonces el centroide debe estar en algún lugar de ese plano. Si el volumen tiene más de un plano de simetría, el centroide debe existir en la intersección de esos planos.

Encontrar el centro de masa para formas de densidad no uniforme

Si un cuerpo tiene una densidad no uniforme, entonces el centroide del volumen y el centro de masa ya no serán el mismo punto. En estos casos, estaremos integrando con respecto a la masa, en lugar de integrar el volumen. Para ello, usaremos algo llamado función de densidad, que proporcionará la densidad (la masa por unidad de volumen) en términos de la\(x\),\(y\), y/o\(z\) ubicación. Al final, también estaremos dividiendo por masa total, en lugar de dividirnos por volumen total. Las ecuaciones generalizadas para el centro de masa se muestran en las siguientes ecuaciones.

\[ C \neq G \]

\[ G = (x_G, y_G, z_G) \]

\ begin {align} x_g &=\ dfrac {\ int_m (dm*x)} {m} =\ dfrac {\ int_v (\ rho (x, y, z) * dV* x)} {m}\\ [4pt] Y_g &=\ dfrac {\ int_m (dm*y)} {m} =\ dfrac {int_m (dm*y)} {m} =\ dfrac {int_m (dm*y)} {m} = _v (\ rho (x, y, z) * dV * y)} {m}\\ [4pt] z_g &=\ dfrac {\ int_m (dm*z)} {m} =\ dfrac {\ int_v (\ rho (x, y, z) * dV * z)} {m}\ end {align}

En casos de densidad uniforme (donde la función de densidad no variaba con la ubicación y por lo tanto era solo una constante), la constante de densidad se podía mover fuera de la integral. En la parte inferior, también podríamos escribir masa como densidad por volumen, y los términos de densidad en la parte superior e inferior de la fracción se cancelarían. Es por ello que para las piezas de densidad uniforme, el centroide y el centro de masa serán el mismo punto.

Cuando tenemos una función de densidad que no es una constante, tendremos que llegar a una función matemática para la densidad en términos de\(x\) y/o\(y\) y/o\(z\) ubicaciones. Si la densidad varía a lo largo de más de un eje, determinar la función y luego integrarla puede resultar bastante difícil, y el modelado por computadora puede ser aconsejable en estas situaciones.

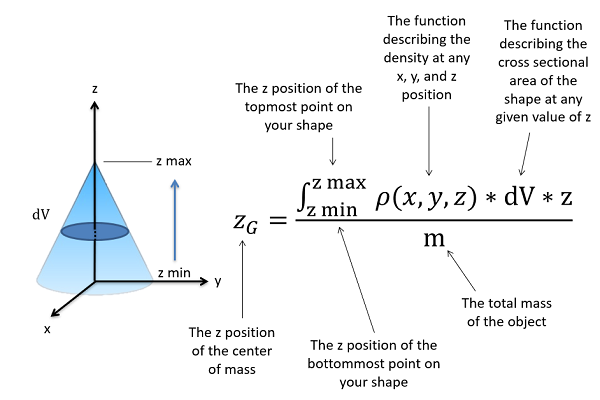
Una vez que tenga la función de densidad, la multiplicará por la\(dV\) función relevante como se discutió anteriormente en la página y la multiplicará por la variable para el eje relevante. Toda esta función se integra de izquierda a derecha, de abajo hacia arriba o de atrás hacia adelante, y luego esa cantidad se divide por masa para encontrar la ubicación del centro de masa.

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/cBiWKfBLEhk.

Ejemplo\(\PageIndex{1}\)

El cono que se muestra a continuación mide cuatro pulgadas de alto y tiene una base de cuatro pulgadas de diámetro. Encuentra las\(z\) coordenadas\(x\)\(y\),, y del centroide.

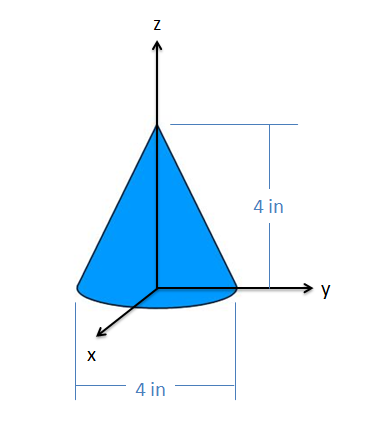
Un cono circular derecho con radio de 2 pulgadas tiene su base ubicada en el plano XY, centrada en el origen. Su punta se encuentra en el eje z, 4 pulgadas por encima de la base. — Figura\(\PageIndex{5}\): diagrama de problemas para Ejemplo\(\PageIndex{1}\). Un cono tiene una base circular centrada en el\(xy\) plano de un sistema de coordenadas cartesianas, y un eje central que se extiende a lo largo del\(z\) eje positivo.

Solución:: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/IJHwNaOG4-s.

Ejemplo\(\PageIndex{2}\)

Encuentra la coordenada y del centroide para el tetraedro que se muestra en la imagen de abajo. (El cuarto vértice está en el origen)

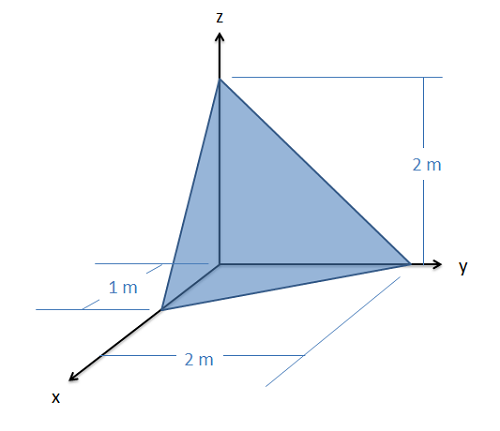
Un tetraedro en el primer octante de un sistema de coordenadas cartesianas tiene vértices ubicados en los puntos (0, 0, 0), (1, 0, 0), (0, 2, 0) y (0, 0, 2). Todas las unidades están en metros. — Figura\(\PageIndex{6}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\). Un tetraedro se encuentra en el primer octante de un sistema de coordenadas cartesianas, con tres de sus bordes formados por los ejes de coordenadas.

Solución:: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/itu_P4ysw9g.

Ejemplo\(\PageIndex{3}\)

Una suspensión de agua y cerámica con una densidad uniforme de 1100 kilogramos por metro cúbico ingresa a un tanque de sedimentación con una altura de 1 metro y un diámetro de 1 metro. Después de una hora en el tanque, la densidad de la suspensión en la parte superior del tanque se mide para ser de 1000 kilogramos por metro cúbico y la densidad en el fondo del tanque se mide para ser de 1200 kilogramos por metro cúbico. Supongamos que la densidad de la suspensión varía linealmente entre la parte superior y la parte inferior. ¿Hasta dónde ha caído el centro de masa de la suspensión entre las condiciones iniciales y el estado actual?

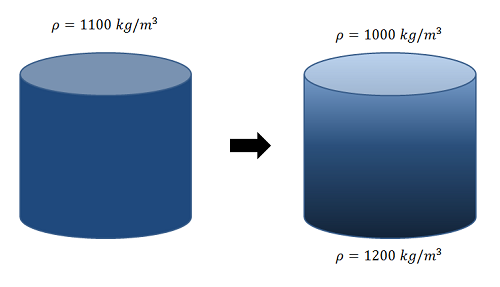
Un cilindro de la izquierda está uniformemente coloreado de un azul medio, y tiene una densidad uniforme de 1100 kg/m³. Un cilindro de tamaño idéntico a la derecha representa el tanque después de 1 hora; el color de este cilindro es un gradiente constante de azul claro en la parte superior a azul oscuro en la parte inferior. La densidad de la parte superior de este tanque es de 1000 kg/m³, y la densidad del fondo es de 1200 kg/m³. — Figura\(\PageIndex{7}\): diagrama de problemas para Ejemplo\(\PageIndex{3}\). A medida que las partículas en un tanque se asientan, una solución de densidad originalmente uniforme se convierte en una con densidad linealmente decreciente de abajo hacia arriba.

Solución:: Video\(\PageIndex{4}\): Solución trabajada a problema de ejemplo\(\PageIndex{3}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/BTyO2HolIHY.