Inicio
Ingeniería
Ingeniería Mecánica
Mapa Mecánico (Moore et al.)
17: Apéndice 2 - Integrales de momento
17.4: Centroides y Centros de Masa a través del Método de Partes Compuestas

17.4: Centroides y Centros de Masa a través del Método de Partes Compuestas

Última actualización
Guardar como PDF

Page ID: 84008

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Como alternativa al uso de integrales de momento, podemos usar el Método de Partes Compuestas para encontrar el centroide de un área o volumen o el centro de masa de un cuerpo. Este método suele ser más fácil y rápido que el método de integración; sin embargo, estará limitado por la tabla de centroides que tenga disponible. El método funciona dividiendo la forma o el volumen en varias formas más básicas, identificando los centroides o centros de masas de cada parte a través de una tabla de valores, y luego peinando los resultados para encontrar el centroide general o centro de masa.

Un aspecto clave del método es el uso de estas tablas centroides. Este es un conjunto de tablas que enumera los centroides (y generalmente también momentos de inercia) para una serie de áreas comunes y/o volúmenes. Algunas tablas centroides se pueden encontrar aquí para formas 2D, y aquí para formas 3D. El método de las piezas compuestas es limitado ya que necesitaremos poder romper nuestra forma compleja completamente en formas que se encuentran en la tabla centroide que tenemos disponible; de lo contrario, el método no funcionará sin que nosotros también hagamos algunas integrales de momento.

Encontrar el centroide a través del método de piezas compuestas

Comienza el proceso etiquetando un punto de origen y ejes en tu forma. Será importante medir todas las ubicaciones desde un mismo punto. A continuación, debemos romper nuestra forma compleja en varias formas más simples. Esto puede incluir áreas o volúmenes (que contaremos como áreas o volúmenes positivos) o agujeros (que contaremos como áreas o volúmenes negativos). Cada una de estas formas tendrá un centroide (\(C\)) o centro de masa (\(G\)) listado en el diagrama.

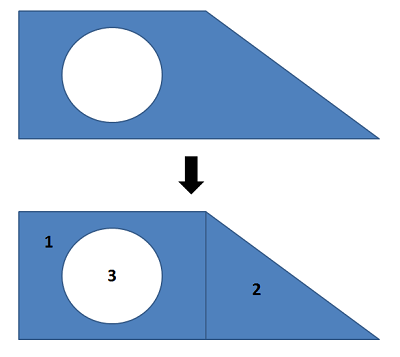
Una forma consiste en un trapecio con bases horizontales, donde el punto final izquierdo de la base superior más corta está directamente por encima del punto final izquierdo de la base más larga, y un agujero redondo a través de la sección izquierda del trapecio. La forma se divide entonces en tres formas más simples: el trapecio se convierte en un rectángulo más un triángulo rectángulo, hecho dividiendo verticalmente el trapecio en el punto donde termina la base más corta, y un círculo para el agujero, que se ubica dentro de la subsección rectangular. — Figura\(\PageIndex{1}\): Para la forma que se muestra en la parte superior, podemos dividirla en un rectángulo (1), un triángulo rectángulo (2) y un agujero circular (3). Cada una de estas formas simples es algo que hemos enumerado en la tabla centroide a la derecha.

Una vez que hayamos identificado las diferentes partes, crearemos una tabla listando el área o volumen de cada pieza,\(x\) y las coordenadas y\(y\) centroide (o\(x\)\(y\), y\(z\) coordenadas en 3D). Es importante recordar que cada coordenada que enumere debe ser relativa al mismo punto de origen base que dibujó anteriormente. Es posible que deba ajustar mentalmente los diagramas en las tablas centroides para que la forma esté orientada en la dirección correcta, y dar cuenta de la ubicación de la forma en relación con los ejes en su diagrama.

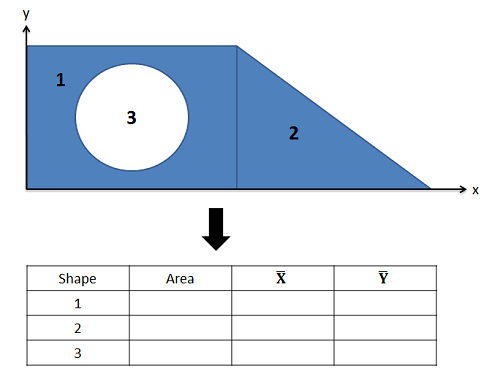
La forma de la Figura 1 anterior, dividida en las secciones 1 a 3, se coloca en el primer cuadrante de un plano de coordenadas cartesianas con la base más larga a lo largo del eje x y el lado vertical del trapecio a lo largo del eje y. A continuación se coloca una tabla con espacios para el área, coordenada x del centroide y coordenada y del centroide de cada una de las 3 subsecciones. — Figura\(\PageIndex{2}\): Para cada una de las formas, necesitamos encontrar el área y las\(y\) coordenadas\(x\) y del centroide. Recuerda encontrar las coordenadas del centroide relativas a un solo conjunto de ejes que es el mismo para todas las formas.

Una vez que tengas las áreas y coordenadas centroides para cada forma en relación con tu punto de origen, puedes encontrar la\(y\) coordenada\(x\) y del centroide para la forma general con las siguientes fórmulas. Recuerda que las áreas o volúmenes para cualquier forma que sea un agujero o recorte en el diseño serán un área negativa en tu fórmula.

\[ \bar{x}_{total} = \frac{\sum A_i \bar{x}_i}{A_{total}} \quad\quad\quad \bar{y}_{total} = \frac{\sum A_i \bar{y}_i}{A_{total}} \]

Esta fórmula generalizada para encontrar la\(x\) ubicación del centroide es simplemente Área 1 veces\(\bar{x}_1\), más Área 2 veces\(\bar{x}_2\), más Área 3 veces\(\bar{x}_3\), sumando tantas formas como tengas de esta manera y luego dividiendo por el área general de tu forma combinada. Las ecuaciones son las mismas para la\(y\) -ubicación del centroide general, excepto que en su lugar usarás\(\bar{y}\) valores en tus ecuaciones.

Para centroides en tres dimensiones simplemente usaremos volúmenes en lugar de áreas, y tendremos una\(z\) coordenada para nuestro centroide así como las\(y\) coordenadas\(x\) y.

Encontrar el centro de masa a través del método de piezas compuestas

Para utilizar el método de piezas compuestas para encontrar el centro de masa, simplemente necesitamos ajustar ligeramente el proceso. Primero, los cálculos del centro de masa siempre estarán en tres dimensiones. Dibuja un punto de origen y algunos ejes en tu diagrama que hicimos para el centroide. Mediremos todas las ubicaciones relativas a este punto de origen. Entonces tendremos que romper la forma compleja en volúmenes simples, siendo cada volumen simple algo en la tabla centroide que tenemos disponible. Recuerda que cuando tenemos una parte con un material uniforme, el centroide y el centro de masa son el mismo punto, por lo que muchas veces hablaremos de estos indistintamente.

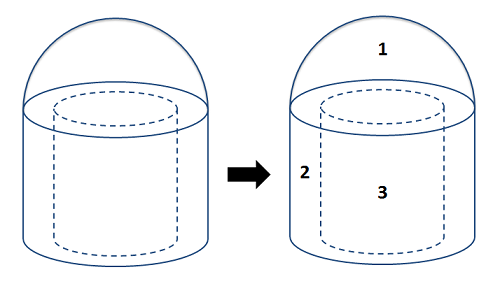
Un objeto tridimensional consiste en un cilindro circular vertical con un orificio que lo atraviesa longitudinalmente, y un hemisferio sólido montado en el lado de la base hacia abajo en la parte superior plana del cilindro. El objeto se divide entonces en tres formas separadas, etiquetadas como 1 - el hemisferio, 2 - el cilindro grande, y 3 - el agujero cilíndrico en el cilindro grande. — Figura\(\PageIndex{3}\): Al encontrar el centro de masa a través de piezas compuestas, vamos a romper la forma en varias formas más simples. La figura de la izquierda puede pensarse como un hemisferio (1), encima de un cilindro (2) con otro cilindro más pequeño cortado de él (3). Cada uno de estos volúmenes simples se enumeran en nuestra tabla centroide.

Una vez que hayamos identificado las diferentes partes, crearemos una tabla que indica la masa de cada parte, y las coordenadas x, y y z del centro de masa para cada parte individual. Es importante recordar que cada coordenada que enumere debe ser relativa al mismo punto de origen base, por lo que necesitará rotar mentalmente y posicionar las partes de la tabla sobre sus ejes.

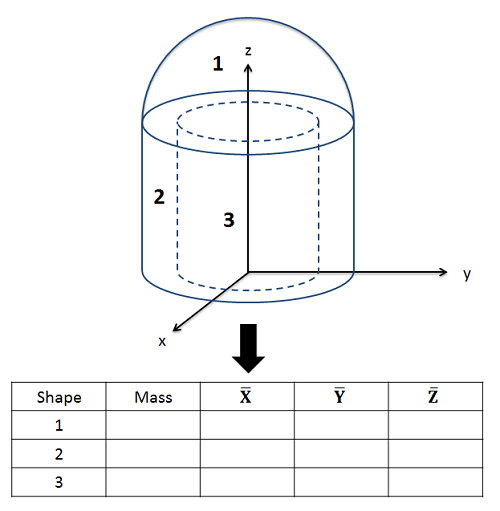
El objeto de la Figura 3 anterior se coloca sobre un sistema de coordenadas cartesianas tridimensionales, con el eje x saliendo de la pantalla, el eje y acostado horizontalmente en el plano de la pantalla, y el eje z tendido verticalmente en el plano de la pantalla. La base plana del cilindro está en el plano XY, centrada en el origen, y la forma se estira hacia arriba a lo largo del eje z positivo. Una tabla debajo de la forma contiene espacios para la masa y la coordenada x, la coordenada y y la coordenada z del centro de masa para cada una de las tres subsecciones de la forma. — Figura\(\PageIndex{4}\): Crear una tabla con la masa de cada pieza de la forma total, así como la ubicación del centro de masa (\(x\),\(y\), y\(z\) coordenadas) para cada pieza.

Un factor que complica con la masa puede ser medir la masa de las piezas por separado. Si tenemos una escala, podemos simplemente conocer la masa general sin conocer la masa de las piezas individuales. En estos casos, es posible que necesite trabajar hacia atrás para calcular la densidad del material (dividiendo la masa total por el volumen total), y luego usar densidad por volumen de pieza para encontrar la masa de cada pieza individualmente. Al hacer esto, recuerde contar los recortes como masa negativa en sus cálculos. Por ejemplo, para el cilindro hueco en la forma anterior, encontraría la masa de un cilindro sólido para la Forma 2, luego tendría una masa negativa para el recorte cilíndrico para la Forma 3.

Finalmente, una vez que tengas la masa las coordenadas y centro de masa para cada forma, puedes encontrar las coordenadas del centro de masa para el volumen general con las siguientes fórmulas.

\[ x_G = \frac{\sum m_i \bar{x}_i}{m_{total}} \quad\quad y_G = \frac{\sum m_i \bar{y}_i}{m_{total}} \quad\quad z_G = \frac{\sum m_i \bar{z}_i}{m_{total}} \]

Similar a las ecuaciones centroides, la\(x\) ecuación -es simplemente la masa de Forma 1 veces\(\bar{x}_1\), más la masa de Forma 2 veces\(\bar{x}_2\), y así sucesivamente para cada parte. Después de haber resumido estos productos para todas las formas, solo divídalos por la masa total.

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/wfjLNSfPXAI.

Ejemplo\(\PageIndex{1}\)

Encuentra las\(y\) coordenadas\(x\) y del centroide de la forma que se muestra a continuación.

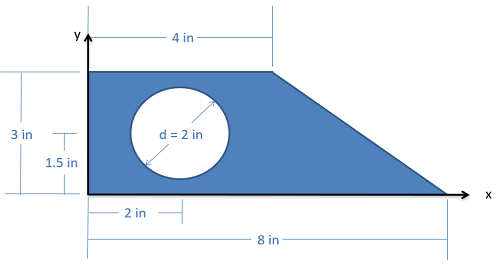
El primer cuadrante de un plano coordenado cartesiano, con la esquina inferior izquierda de un trapecio tendido sobre el origen. Una base del trapecio es de 8 pulgadas de largo y se encuentra a lo largo del eje x. Uno de los otros lados tiene 3 pulgadas de largo y se encuentra a lo largo del eje y. La segunda base del trapecio es de 4 pulgadas de largo y es paralela al eje x. Un agujero circular de 2 pulgadas de diámetro atraviesa esta forma; el orificio está centrado en el punto 1.5 pulgadas arriba y 2 pulgadas a la derecha del origen. — Figura\(\PageIndex{5}\): diagrama de problemas para Ejemplo\(\PageIndex{1}\). Un trapecio con dos lados perpendiculares y un agujero a través de su centro se encuentra a lo largo de los ejes del primer cuadrante de un plano de coordenadas cartesianas.

Solución:: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/QIe6Hk4Bofs.

Ejemplo\(\PageIndex{2}\)

Encuentra las\(y\) coordenadas\(x\) y del centroide de la forma que se muestra a continuación.

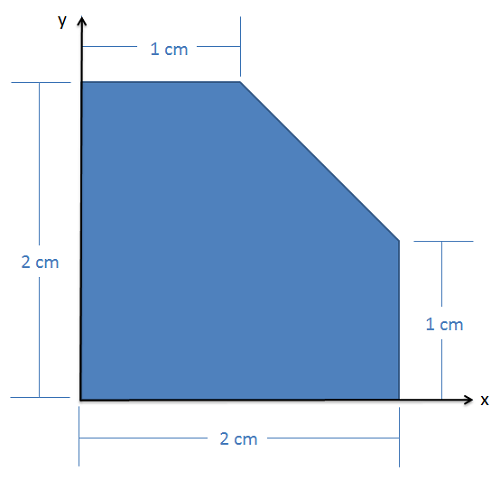
El primer cuadrante de un plano coordenado cartesiano, con la esquina inferior izquierda de un pentágono en el origen. Un lado del pentágono, de 2 cm de largo, se extiende a lo largo del eje x y su extremo derecho se conecta a un lado vertical de 1 cm de largo. Otro lado, también de 2 cm de largo, se extiende a lo largo del eje y; su extremo superior se conecta a un lado horizontal de 1 cm de largo. El quinto lado conecta los dos lados de 1 cm. — Figura\(\PageIndex{6}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\). Un pentágono con dos lados perpendiculares se encuentra a lo largo de los ejes del primer cuadrante de un plano de coordenadas cartesianas.

Solución:: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/F1rlzboPlZM.

Ejemplo\(\PageIndex{3}\)

Encuentra las\(y\) coordenadas\(x\) y del centroide de la forma que se muestra a continuación.

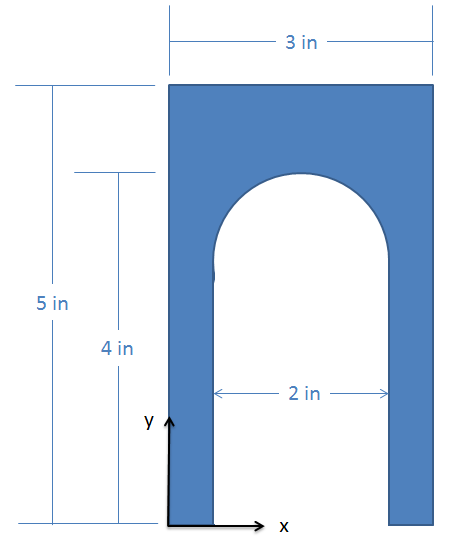
El primer cuadrante de un plano coordenado cartesiano, con la esquina inferior izquierda de un rectángulo en el origen. Un lado del rectángulo mide 3 pulgadas de largo y se encuentra a lo largo del eje x. Otro lado tiene 5 pulgadas de largo y se encuentra a lo largo del eje y. Un recorte rectangular de 2 pulgadas de ancho y 3 pulgadas de alto, coronado por un semicírculo de 2 pulgadas de diámetro, está centrado horizontalmente sobre el rectángulo sólido, comenzando en el eje x. — Figura\(\PageIndex{7}\): diagrama de problemas para Ejemplo\(\PageIndex{3}\). Un rectángulo con un agujero a través de un lado (con forma de rectángulo rematado con un semicírculo) se encuentra a lo largo de los ejes del primer cuadrante de un plano de coordenadas cartesianas.

Solución:: Video\(\PageIndex{4}\): Solución trabajada a problema de ejemplo\(\PageIndex{3}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/tLybTEX8S_I.

Ejemplo\(\PageIndex{4}\)

La forma que se muestra a continuación consiste en un hemisferio semicircular sólido en la parte superior de un cilindro hueco. Con base en las dimensiones siguientes, determine la ubicación del centroide.

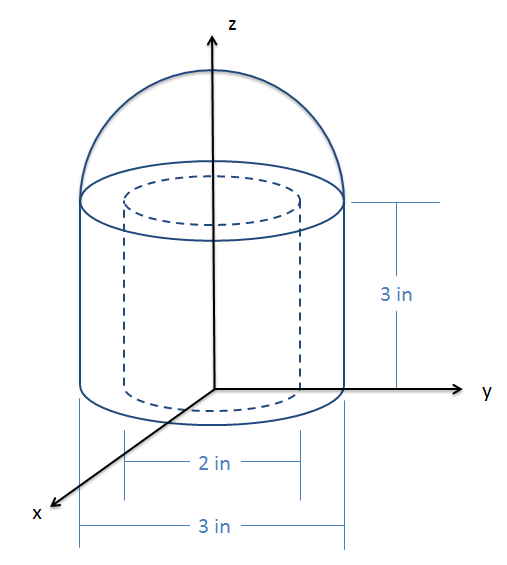
Un plano de coordenadas cartesianas tridimensional, con el eje x apuntando fuera de la pantalla, el eje y acostado horizontalmente en el plano de la pantalla, y el eje z tendido verticalmente en el plano de la pantalla. Un cilindro de 3 pulgadas de alto de diámetro y 3 pulgadas se encuentra con su base en el plano XY, centrado en el origen. Un orificio cilíndrico de 2 pulgadas de diámetro recorre el eje central de este cilindro. Un hemisferio sólido de 3 pulgadas de diámetro se encuentra en la parte superior del cilindro sólido. — Figura\(\PageIndex{8}\): diagrama de problemas para Ejemplo\(\PageIndex{4}\). Un cilindro ahuecado rematado con un hemisferio se encuentra a lo largo del\(z\) eje de un sistema de coordenadas cartesianas, con su base centrada en el\(xy\) plano.

Solución:: Video\(\PageIndex{5}\): Solución trabajada a problema de ejemplo\(\PageIndex{4}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/vQk4OqTcDpQ.

Ejemplo\(\PageIndex{5}\)

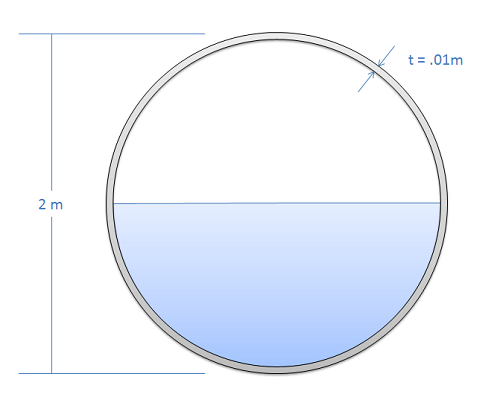
Un tanque esférico de acero (densidad = 8050 kg/m ³) se llena hasta la mitad con agua (densidad = 1000 kg/m ³) como se muestra a continuación. Encuentra la masa total del tanque y la ubicación actual del centro de masa del tanque (medida desde la base del tanque).

Un tanque esférico de acero tiene un diámetro de 2 metros y un espesor de metal de 0.01 metros. El tanque está medio lleno de agua. — Figura\(\PageIndex{9}\): diagrama de problemas para Ejemplo\(\PageIndex{5}\). Un tanque esférico de acero de diámetro 2 metros y espesor de metal 0.01 metros está medio lleno de agua.

Solución:: Video\(\PageIndex{6}\): Solución trabajada a problema de ejemplo\(\PageIndex{5}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/5zbYD4Wogck.