17.5: Momentos de inercia de área vía integración

Última actualización
Guardar como PDF

Page ID: 84028

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Los momentos de inercia de área se utilizan en cursos de mecánica de ingeniería para determinar la resistencia de un cuerpo a cargas de flexión o cargas torsionales. Específicamente, el momento de inercia de área se refiere al segundo momento de área integral de una forma, con\(I_{xx}\) representar el momento de inercia alrededor del\(x\) eje -eje,\(I_{yy}\) representando el momento de inercia alrededor del\(y\) -eje, y\(J_{zz}\) (también llamado el momento polar de inercia) que representa el momento de inercia alrededor del\(z\) eje. El momento de inercia alrededor de cada eje representa la resistencia de las formas a un momento aplicado alrededor de ese eje respectivo. Los momentos sobre los\(y\) ejes\(x\) - y -tenderían a doblar un objeto, mientras que los momentos alrededor del\(z\) eje tenderían a torcer el cuerpo.

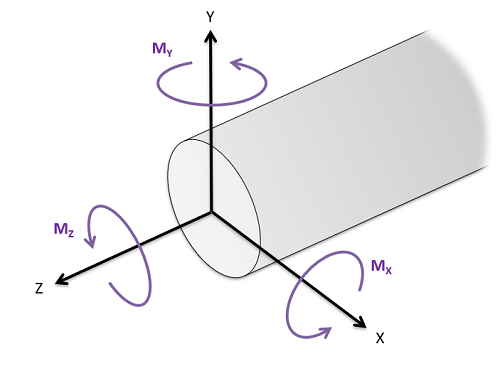
Un cilindro se encuentra con su eje central a lo largo del eje z de un sistema de coordenadas cartesianas tridimensional. Si el cilindro experimenta un momento de inercia alrededor de los ejes x o y, se está doblando. Si el cilindro experimenta un momento de inercia alrededor del eje z, está siendo torcido. — Figura\(\PageIndex{1}\): Los momentos de inercia para la sección transversal de una forma alrededor de cada eje representan la resistencia de la forma a los momentos alrededor de ese eje. Los momentos aplicados alrededor del\(x\) eje -eje y\(y\) -eje representan momentos de flexión, mientras que los momentos alrededor del eje\(z\) - representan momentos torsionales.

Al igual que con los centroides, cada uno de estos momentos de inercia se puede calcular a través de la integración o utilizando el método de partes compuestas y el teorema del eje paralelo. En esta página nos vamos a centrar en calcular los momentos de inercia del área a través de integrales de momento.

Las tensiones de flexión y el momento de la segunda área

Cuando un objeto se somete a un momento de flexión, ese cuerpo experimentará tanto tensiones internas de tracción como tensiones de compresión como se muestra en el diagrama a continuación. Estas tensiones ejercen un momento neto para contrarrestar el momento de carga, pero no ejercen ninguna fuerza neta para que el cuerpo permanezca en equilibrio.

Una vista lateral de una viga horizontal muestra que experimenta un momento de flexión en el sentido de las agujas del reloj en su extremo izquierdo. En el borde derecho de la viga, esto da como resultado fuerzas de compresión hacia la izquierda en la mitad superior, equilibradas por las fuerzas de tracción hacia la derecha en la mitad inferior. El plano horizontal dentro de la viga donde ocurre este interruptor en la dirección de estas fuerzas se llama superficie neutra. Una sección transversal de la misma viga muestra que cualquier sección pequeña de área en la sección transversal estará a una distancia de d de la superficie neutra. — Figura\(\PageIndex{2}\): Momento de flexión y las tensiones internas resultantes de tracción y compresión necesarias para asegurar que la viga esté en equilibrio.

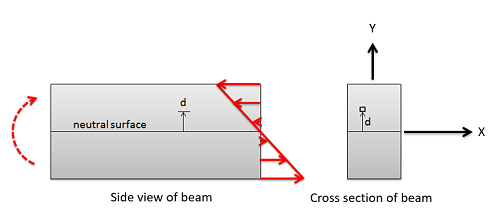
Como podemos ver en el diagrama, hay algún plano central a lo largo del cual no hay tensiones de tracción o compresión. Esto se conoce como la superficie neutra, y si no hay otras fuerzas presentes correrá por el centroide de la sección transversal. A medida que nos movemos hacia arriba o hacia abajo desde la superficie neutra, las tensiones aumentan linealmente. El momento que ejerce esta tensión en cualquier punto será el esfuerzo multiplicado por el brazo de momento, que también aumenta linealmente a medida que nos alejamos de la superficie neutra. Esto significa que la resistencia a la flexión proporcionada por cualquier punto de la sección transversal es directamente proporcional a la distancia desde el eje neutro al cuadrado. Podemos resumir las resistencias a la flexión luego usando el segundo momento de inercia de área rectangular, donde nuestras distancias se miden desde el eje neutro.

\[ I = \int_A (dA * d^2) \]Suponiendo que ponemos el punto de origen en el centroide y que el\(x\) eje -eje es la superficie neutra, la distancia desde la superficie neutra a cualquier punto es simplemente la\(y\) coordenada de ese punto. De igual manera, si aplicamos un momento alrededor del\(y\) eje -eje, y tuviéramos una superficie neutra que corría a lo largo del\(y\) eje -eje, la distancia desde el eje neutro sería simplemente la\(x\) coordenada del punto. Por esta razón,\(I_{xx}\) incluye\(y\) como la distancia, mientras que\(I_{yy}\) incluye\(x\) como la distancia.

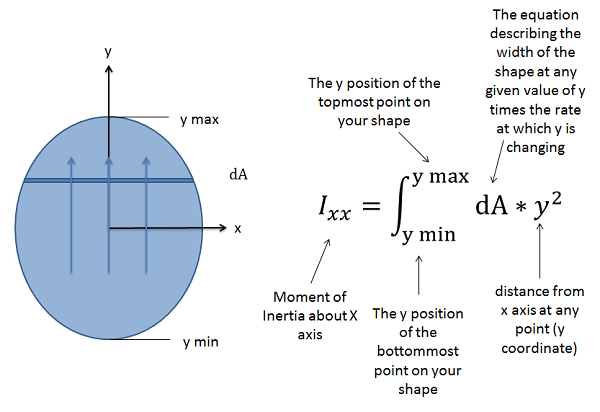
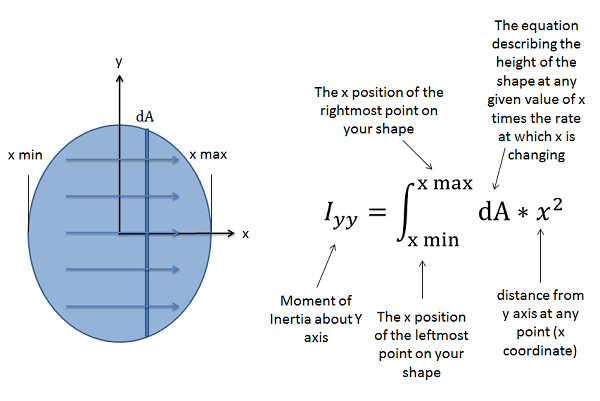
\[ I_{xx} = \int_{y_{min}}^{y_{max}} (dA * y^2) \quad\quad\quad I_{yy} = \int_{x_{min}}^{x_{max}} (dA * x^2) \]

Cálculo del Momento de Inercia de Área Rectangular vía Integración

Para determinar el momento de inercia del área, comience dibujando el área bajo análisis, e incluya los ejes sobre los que está tomando el momento de inercia. Esto es importante, ya que el momento de inercia variará dependiendo del eje elegido. En los casos en tensiones de flexión querrás poner el origen en la superficie neutra, que estará en el centroide de la zona. Si no se le da el centroide, deberá determinar el centroide como se discutió en secciones anteriores.

Para tomar el momento de inercia alrededor del\(x\) eje -a través de este punto (\(I_{xx}\)) utilizaremos la fórmula general discutida anteriormente. Estaremos moviéndonos de abajo hacia arriba, integrando la tasa de cambio del área a medida que avanzamos, y multiplicando eso por el\(y\) -valor al cuadrado. La tasa de cambio de area (\(dA\)) a medida que nos movemos hacia arriba será el ancho del objeto a cualquier\(y\) valor dado multiplicado por la velocidad a la que nos movemos. A menos que el ancho permanezca constante, el ancho deberá representarse como una función matemática en términos de\(y\).

Una elipse con su centroide ubicada en el origen de un plano de coordenadas cartesianas. Para encontrar el momento de inercia alrededor del eje x, la elipse se divide en muchas tiras delgadas y horizontales de y constante, teniendo cada tira el área dA. El momento alrededor del eje x se encuentra integrando el producto de dA y el cuadrado de la coordenada y (que es la distancia desde el eje x) desde el valor y mínimo hasta el valor y máximo cubierto por la elipse. — Figura\(\PageIndex{3}\): Momento rectangular de inercia alrededor del\(x\) eje.

Para encontrar el momento de inercia alrededor del\(y\) eje -a través de un punto dado (\(I_{yy}\)) nos desplazaremos de izquierda a derecha, utilizando las distancias desde el\(y\) eje -en nuestro momento integral (en este caso las\(x\) coordenadas de cada punto). Moviéndose de izquierda a derecha, la tasa de cambio del área será la altura de la forma en cualquier\(x\) valor dado multiplicado por la velocidad a la que nos movemos de izquierda a derecha. Nuevamente, tendremos que describir esto con una función matemática si la altura no es constante. Multiplicaremos esta función por el\(x\) -valor al cuadrado para el segundo momento integral, y esto nos dará el momento de inercia alrededor del\(y\) eje -eje.

Una elipse con su centroide ubicada en el origen de un plano de coordenadas cartesianas. Para encontrar el momento de inercia alrededor del eje y, la elipse se divide en muchas tiras delgadas y horizontales de x constante, teniendo cada tira el área dA. El momento alrededor del eje y se encuentra integrando el producto de dA y el cuadrado de la coordenada x (que es la distancia desde el eje y) desde el valor x mínimo hasta el valor x máximo cubierto por la elipse. — Figura\(\PageIndex{4}\): Momento rectangular de inercia alrededor del\(y\) eje.

Las tensiones torsionales y el momento polar de inercia

Cuando un objeto es sometido a un momento de torsión, ese objeto experimentará fuerzas de corte internas como se muestra en el diagrama a continuación. Estas tensiones están orientadas de tal manera que contrarrestarán el momento torsional, pero no ejercerán ninguna fuerza neta sobre el eje para que el eje permanezca en equilibrio.

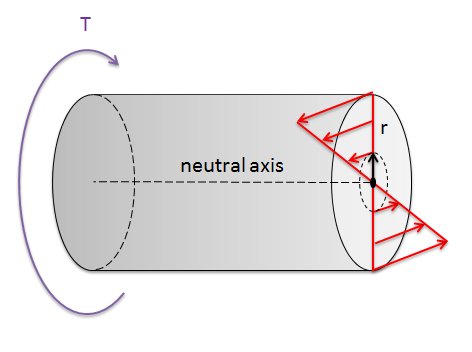
Un cilindro horizontal experimenta un momento de torsión girándolo hacia la página. El cilindro exhibe fuerzas internas que resisten esta rotación: la mitad superior del cilindro ejerce fuerzas que apuntan hacia fuera de la página, resistiendo ser girado hacia la página, mientras que la mitad inferior ejerce fuerzas que apuntan hacia la página, resistiendo ser girado fuera de la página. El eje central del cilindro, también llamado eje neutro, no experimenta fuerzas en ninguna dirección. La distancia de un punto en el cilindro desde el eje neutro se puede expresar con la coordenada polar r. — Figura\(\PageIndex{5}\): La torsión provoca esfuerzos de corte internos que contrarrestan el momento pero no ejercen fuerza neta.

Como podemos ver en el diagrama, hay un eje central a lo largo del cual no hay esfuerzos de cizallamiento. Esto se conoce como eje neutro, y si no hay otras fuerzas presentes, entonces éste viajará a través del centroide de la sección transversal del eje. A medida que nos alejamos del eje neutro en cualquier dirección, las tensiones aumentarán linealmente. El momento ejercido por la tensión en cualquier punto será el esfuerzo multiplicado por el brazo de momento, que también aumenta linealmente a medida que nos alejamos del eje neutro. Esto significa que la resistencia a la carga torsional proporcionada por cualquier punto en la sección transversal es directamente proporcional al cuadrado de la distancia entre el punto y el eje neutro. Podemos resumir las resistencias a la carga torsional luego usando el segundo momento de inercia de la zona polar, donde nuestras distancias se miden desde el eje neutro (\(r\)), un solo punto en la sección transversal del eje.

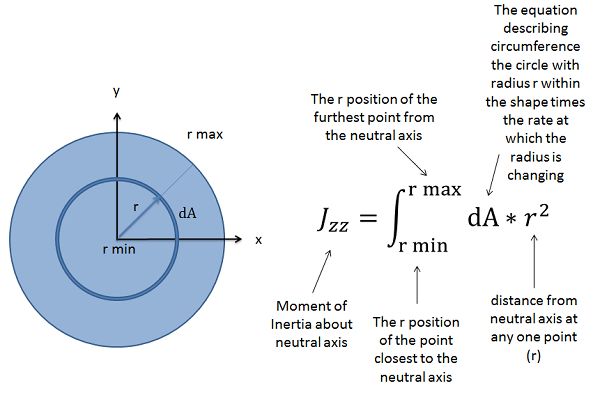
\[ J_{zz} = \int_{r_{min}}^{r_{max}} (dA * r^2) \]

Cálculo del Momento de Inercia del Área Polar vía Integración

El primer paso para determinar el momento polar de inercia es dibujar el área e identificar el punto sobre el que estamos tomando el momento de inercia. En el caso de la carga torsional, normalmente vamos a querer escoger el punto en el que el eje neutro recorre la sección transversal del eje, que a falta de otro tipo de carga será el centroide de la sección transversal. Si el centroide no está claramente identificado, deberá determinar el centroide como se discutió en secciones anteriores.

Para tomar el momento de inercia sobre este punto central, estaremos midiendo todas las distancias hacia afuera desde este punto. En lugar de movernos de izquierda a derecha o de arriba a abajo, en cambio estaremos integrándonos desde el centro irradiando hacia afuera en todas las direcciones. Vamos a ir desde la distancia mínima del centro para nuestra forma (cero a menos que haya un agujero central en nuestra zona) hasta la distancia máxima al centro. Nuevamente estaremos integrando la tasa de cambio de área, que en este caso será una función para la circunferencia en un radio dado multiplicado por la velocidad como la que nos estamos moviendo hacia afuera por el radio dado al cuadrado.

Una sección transversal de un cilindro sólido tiene su punto central ubicado en el origen de un plano de coordenadas cartesianas. Para encontrar el momento de inercia alrededor del eje neutro del cilindro, la sección transversal se divide en muchos anillos delgados de radio constante r, todos centrados en el origen. Cada anillo tiene el área dA. El momento de inercia alrededor del eje neutro se encuentra integrando dA veces r al cuadrado desde el valor r mínimo (que es 0 en este caso) hasta el valor r máximo (el radio del propio cilindro). — Figura\(\PageIndex{6}\): Momento polar de inercia alrededor del eje neutro.

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/gCM6Wd8sa6M.

Ejemplo\(\PageIndex{1}\)

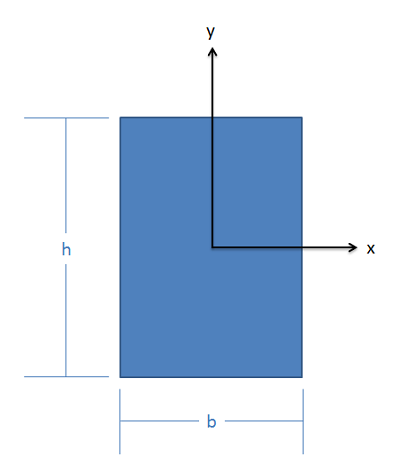
Encuentra los momentos rectangulares de inercia para esta forma alrededor del\(x\) eje -y\(y\) -eje a través del centroide. Deja la respuesta en términos de la anchura genérica (\(b\)) y la altura (\(h\)) del rectángulo.

Un rectángulo de ancho b y alto h tiene su centroide ubicado en el origen de un plano de coordenadas cartesianas y sus lados paralelos a los ejes. — Figura\(\PageIndex{7}\): diagrama de problemas para Ejemplo\(\PageIndex{1}\). Un rectángulo sólido se centra en el origen de un plano de coordenadas cartesianas.

Solución:: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/PL6QIBL_rPw.

Ejemplo\(\PageIndex{2}\)

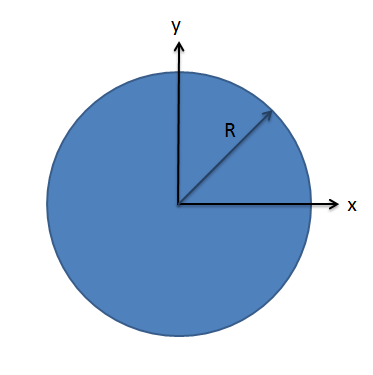
Encuentra los momentos polares de inercia para esta zona circular alrededor de su centroide. Deja la respuesta en términos del radio genérico\(R\).

Un círculo sólido de radio R se centra en el origen de un plano de coordenadas cartesianas. — Figura\(\PageIndex{8}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\). Un círculo sólido se centra en el origen de un plano de coordenadas cartesianas.

Solución:: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/peqSVmDjThA.

Ejercicio\(\PageIndex{3}\)

Encuentra el momento polar de inercia de esta forma circular hueca alrededor de su centroide.

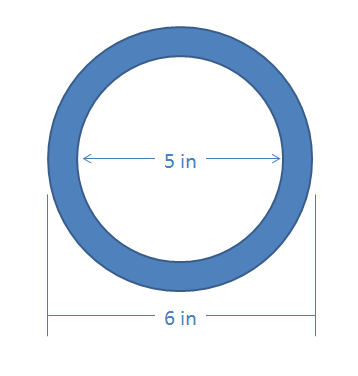
Un disco de 6 pulgadas de diámetro tiene un recorte circular de 5 pulgadas de diámetro que atraviesa su centro. — Figura\(\PageIndex{9}\): diagrama de problemas para Ejemplo\(\PageIndex{3}\). Un disco de 6 pulgadas de diámetro contiene un recorte circular centrado de 5 pulgadas de diámetro.

Solución:: Video\(\PageIndex{4}\): Solución trabajada a problema de ejemplo\(\PageIndex{3}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/Jw696gGSDM8.