17.6: Momentos masivos de inercia a través de la integración

Última actualización
Guardar como PDF

Page ID: 84019

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

El momento de inercia de masa representa la resistencia de un cuerpo a las aceleraciones angulares alrededor de un eje, así como la masa representa la resistencia de un cuerpo a las aceleraciones lineales. Esto se representa en una ecuación con la versión rotacional de la Segunda Ley de Newton.

\[ F = ma \]

\[ M = I \alpha \]

Al igual que con los momentos de inercia de área, el momento de inercia de masa se puede calcular a través de integrales de momento o mediante el método de partes compuestas y el teorema del eje paralelo. Esta página solo discutirá el método de integración, ya que el método de las piezas compuestas se discute en una página separada.

El Momento Masivo de Inercia y Aceleraciones Angulares

El momento de inercia de masa es un momento integral, específicamente el segundo momento de masa polar integral. Para ver por qué esto relaciona momentos y aceleraciones angulares, comenzamos por examinar una masa puntual en el extremo de un palo sin masa como se muestra a continuación. Imagina que queremos rotar el palo sobre el extremo izquierdo aplicando un momento ahí. Queremos relacionar el momento ejercido con la aceleración angular del palo sobre este punto.

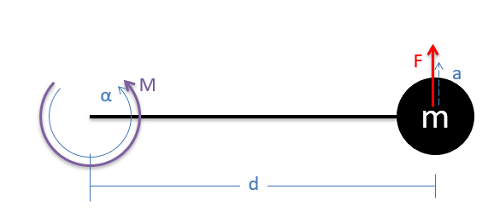
Una barra horizontal de longitud d sostiene una masa puntual en su extremo derecho. Un momento en sentido antihorario y una aceleración angular se aplican al extremo izquierdo del stick, haciendo que la masa puntual experimente una fuerza y una aceleración que apuntan hacia la parte superior de la página. — Figura\(\PageIndex{1}\): Una masa puntual en el extremo de un palo sin masa. Estamos intentando rotar la masa alrededor del extremo izquierdo del palo ejerciendo un momento ahí.

Para relacionar el momento y la aceleración angular, necesitamos comenzar con la forma tradicional de la Segunda Ley de Newton, afirmando que la fuerza ejercida sobre la masa puntual por el palo será igual a la masa multiplicada por la aceleración de la masa puntual (\(F = m*a\)). En este caso el momento estará relacionado con la fuerza en que la fuerza ejercida sobre la masa por la longitud del palo (\(d\)) es igual al momento. También podemos relacionar la aceleración lineal de la masa con su contraparte rotacional en que la aceleración lineal es la aceleración angular multiplicada por la longitud de la varilla (\(d\)). Si tomamos estas dos sustituciones y las ponemos en la\(F = m*a\) ecuación original, podemos terminar con una ecuación que relaciona el momento y la aceleración angular para nuestro escenario. Una versión simplificada de esta nueva relación establece que el momento será igual a la masa por la distancia al cuadrado por la aceleración angular. Este término masa-tiempo-distancia-cuadrado (que relaciona el momento y la aceleración angular) forma la base del momento masivo de inercia.

\[ F = m * a \]

\[ M = F * d \quad\quad\quad a = d * \alpha \]

\[ M = (m * d^2) * \alpha \]

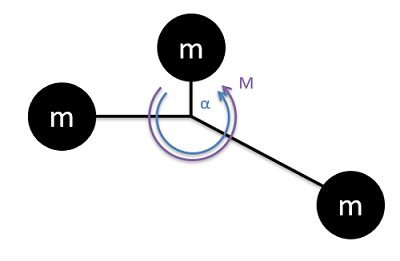
Llevando nuestra situación un paso más allá, si tuviéramos que tener múltiples masas todas conectadas a un punto central, el momento y la aceleración angular estarían relacionados por la suma de todos los términos de masa por distancia al cuadrado.

\[ M = \sum (m * d^2) * \alpha \]

Tres varillas sin masa de diferentes longitudes irradian desde un solo punto, y cada varilla sostiene una masa puntual m en su extremo libre. Se aplica un momento en sentido antihorario al punto central donde se conectan las varillas. — Figura\(\PageIndex{2}\): Para sistemas con múltiples masas, simplemente resumiríamos todos los términos masa-tiempo-distancia-cuadrado para relacionar momentos y aceleraciones angulares.

Dando el paso final, los cuerpos rígidos con masa distribuida sobre un volumen son como un número infinito de pequeñas masas alrededor de un eje de rotación. En lugar de los palos sin masa que sostienen todo en su lugar, la masa simplemente se sostiene en su lugar por el material que la rodea. Para relacionar el momento y la aceleración angular en este caso, utilizamos la integración para sumar el número infinito de pequeños términos masa-tiempo-distancia-cuadrado.

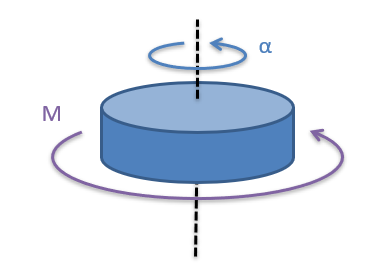
Un cilindro vertical gira en sentido antihorario alrededor de su eje central. — Figura\(\PageIndex{3}\): Aproximando un cuerpo rígido como un número infinito de masas infinitamente pequeñas todas conectadas al eje de rotación, podemos sumar todos los términos masa-tiempo-distancia-cuadrado con integración.

\[ M = \int_m (dm * d^2) * \alpha \]

Esta integral de momento que se puede calcular para cualquier forma dada, llamada momento de inercia de masa, relaciona el momento y la aceleración angular para el cuerpo alrededor de un eje de rotación establecido.

\[ I = \int_m (dm * d^2) \]

Cálculo del Momento de Inercia Masivo vía Integración

El primer paso para calcular el momento de inercia de masa es determinar el eje de rotación que va a utilizar. A diferencia de la masa, el momento de inercia de masa depende del punto y eje sobre el que estamos rotando. Podemos demostrar esto fácilmente con algo así como una escoba, donde dependiendo de la posición y la dirección del eje sobre el que estemos girando, la escoba puede ser más o menos difícil de rotar.

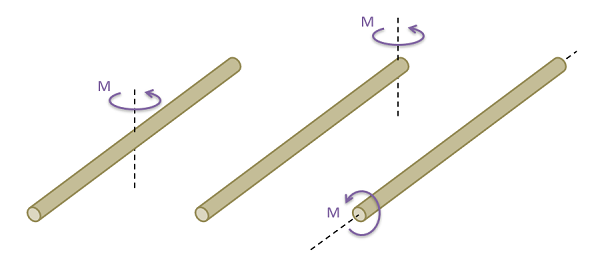
Una escoba en la misma orientación actual tendrá diferentes momentos de inercia de masa dependiendo de si se gira alrededor del punto medio de su longitud, alrededor de un extremo, o alrededor de su eje central. — Figura\(\PageIndex{4}\): El momento de inercia de masa variará dependiendo del punto y dirección del eje de rotación.

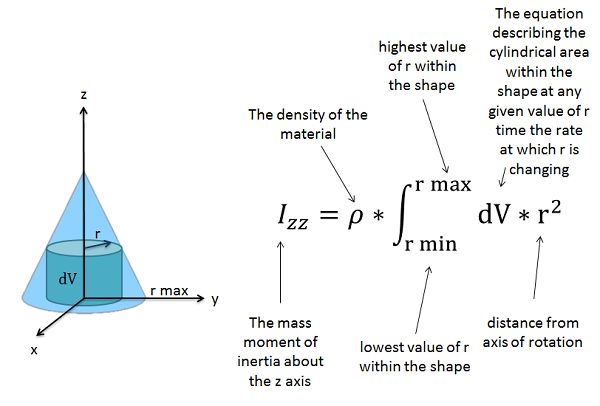
Después de elegir el eje de rotación, es útil dibujar la forma con el eje de rotación incluido. Esta es una integral polar, por lo que estaremos tomando la masa integral que irradia hacia afuera desde este eje de rotación.

También, nos estamos integrando sobre la masa, y la masa en cualquier punto dado será la densidad por el volumen. Si el objeto que estamos examinando tiene una densidad uniforme, como suele ser el caso, podemos tirar de esa densidad constante fuera de la integral, dejando sólo una integral del volumen. La densidad rara vez se da en estos casos, pero si puedes determinar la masa general y el volumen general puedes usar eso también. Si ponemos todo esto en la ecuación original que teníamos arriba, terminamos con lo siguiente.

\[ I = \rho * \int_{r_{min}}^{r_{max}} (dV * r^2) = \frac{m}{V} * \int_{r_{min}}^{r_{max}} (dV * r^2) \]

Para la integral polar, necesitamos definir\(dV\) en términos de un radio (\(r\)) que se mueve hacia afuera desde el eje de rotación. La velocidad de cambio del volumen (\(dV\)) será el área de superficie cilíndrica en un radio dado multiplicado por la velocidad a la que ese radio está aumentando (\(dr\)). La altura, el radio y los agujeros en esta superficie cilíndrica pueden estar cambiando por lo que este\(dV\) término puede llegar a ser bastante complejo, pero técnicamente podríamos encontrar esto para la función matemática para cualquier forma. Una vez que tenemos la\(dV\) función en términos de\(r\), multiplicamos esa función por\(r^2\) y evaluaremos la integral.

Un cono con su base centrada en el plano XY de un sistema de coordenadas cartesianas y su altura que se extiende hacia arriba a lo largo del eje z positivo se divide en conchas cilíndricas delgadas, cada una de un radio constante r medido desde el eje z. El volumen de cada una de estas conchas es dV. El momento de inercia alrededor del eje z es la densidad constante rho veces la integral de dV veces r-cuadrado, evaluada desde el valor r mínimo de la forma hasta su valor r máximo. — Figura\(\PageIndex{5}\): El momento de inercia de masa para una forma general.

Videoconferencia que cubre esta sección, impartida por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/uarIssOmWUU.

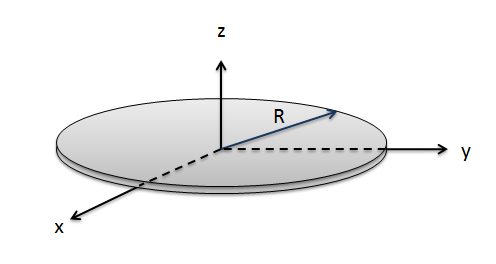
Ejemplo\(\PageIndex{1}\)

Un disco circular delgado tiene una masa de 6 kg y un radio de 0.3 metros. Determinar el momento de inercia de masa para el disco alrededor\(z\) del eje.

Un disco cilíndrico delgado se encuentra en el plano XY de un sistema de coordenadas cartesianas tridimensional, con el eje x apuntando hacia fuera de la pantalla y el eje y acostado horizontalmente en el plano de la pantalla. La base del disco está centrada en el origen y la altura del disco se extiende a lo largo del eje z positivo. — Figura\(\PageIndex{6}\): diagrama de problemas para Ejemplo\(\PageIndex{1}\). Un disco cilíndrico delgado se encuentra a lo largo del\(z\) eje con su base en el\(xy\) plano, centrado en el origen.

Solución:: Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/e1ZDv6xDUV8.

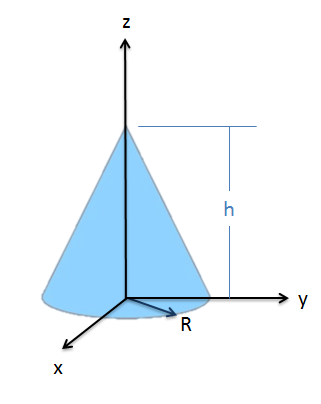
Ejemplo\(\PageIndex{2}\)

Determine el momento de inercia de masa alrededor del\(z\) eje para este cono general con radio base\(R\)\(h\), altura y masa\(m\).

Un sistema de coordenadas cartesianas tridimensional, con el eje x apuntando fuera de la pantalla, el eje y acostado horizontalmente en el plano de la pantalla, y el eje z tendido verticalmente en el plano de la pantalla. Un cono circular derecho se encuentra con su base en el plano XY, centrado en el origen, y su altura se extiende a lo largo del eje z positivo. — Figura\(\PageIndex{7}\): diagrama de problemas para Ejemplo\(\PageIndex{2}\). Un cono se encuentra a lo largo del\(z\) eje positivo, con la base centrada en el origen en el\(xy\) plano -plano.

Solución:: Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Jacob Moore. Fuente de YouTube: https://youtu.be/rL7xWl9FfWc.