1.1: Tensión unidimensional
- Page ID
- 85212
Considera una varilla o viga prismática de espesor uniforme de la longitud inicial\(l_o\). La varilla se fija en un extremo y se somete una fuerza de tracción (Figura (\(\PageIndex{1}\))) en el otro extremo. La longitud actual, deformada se denota por\(l\). La cuestión es si el campo de deformación resultante es homogéneo o no. El concepto de homogeneidad en mecánica significa independencia de la solución sobre el sistema de coordenadas espaciales, el eje de la varilla en el presente caso. Se puede demostrar que si la curva tensión-deformación del material es convexa o lineal, la varilla se deforma uniformemente y se desarrolla un estado homogéneo de deformaciones y tensiones dentro de la varilla. Esto significa que las cepas locales y medias son las mismas y la cepa se puede definir considerando las longitudes totales. El desplazamiento en el extremo fijo\(x = 0\) de la varilla es cero,\(u(x = 0)\) y el desplazamiento final es
\[u(x = l) = l − l_o \label{1.1.1}\]
La deformación se define como un desplazamiento relativo. ¿Relativo a qué? ¿Inicial, longitud actual o algo más? La definición de cepa es simple pero a la vez no es única.
\[\epsilon \buildrel \rm {def} \over{=} \frac{l − l_o}{l_o} \text{ Engineering Strain} \label{1.1.2}\]
\[\epsilon \buildrel \rm {def} \over{=} \frac{1}{2} \frac{l^2 − l_o^2}{l^2} \text{ Cauchy Strain} \label{1.1.3}\]
\[\epsilon \buildrel \rm {def} \over{=} \ln \frac{l}{l_o} \text{ Logarithmic Strain} \label{1.1.4}\]
Cada una de las tres definiciones anteriores satisface el requisito básico de que la deformación se\(l = l_o\) desvanezca cuando o\(u = 0\) y esa tensión en una función creciente del desplazamiento\(u\).
Consideremos un caso limitante de la Ecuación\ ref {1.1.1} para pequeños desplazamientos\(\frac{u}{l_o} \ll 1\), para lo cual\(l_o+l \approx 2l_o\) en la Ecuación\ ref {1.1.3}. Entonces, la cepa Cauchy se convierte en
\[\epsilon = \frac{l − l_o}{l_o} \frac{l + l_o}{2l_o} \cong \frac{l − l_o}{l_o} \frac{2l}{2l_o} \cong \frac{l − l_o}{l_o} \label{1.1.5}\]
Así, para la deformación pequeña, la cepa Cauchy se reduce a la deformación de ingeniería. Asimismo, expandiendo la expresión para la deformación logarítmica, Ecuación\ ref {1.1.4} en la serie Taylor alrededor\(l − l_o \cong 0\),
\[\left. \ln \frac{l}{l_o} \right|_{l/l_o=1} \cong \frac{l − l_o}{l_o} - \frac{1}{2} \left( \frac{l + l_o}{l_o} \right)^2 + \ldots \approx \frac{l − l_o}{l_o}\]
se puede ver que la deformación logarítmica se reduce a la deformación de ingeniería.
Las gráficas de\(\epsilon\) versus\(\frac{l}{l_o}\) según Ecuaciones\ ref {1.1.2} -\ ref {1.1.4} se muestran en la Figura (\(\PageIndex{1}\)).
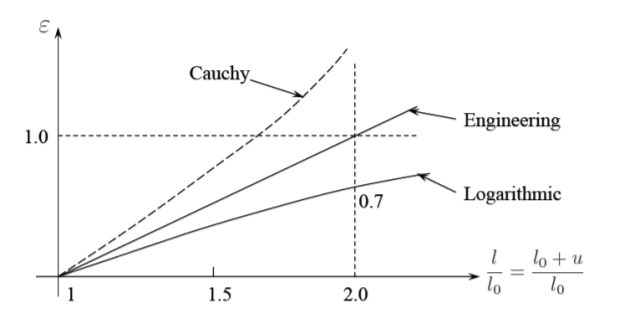
Campo de deformación no homogéneo
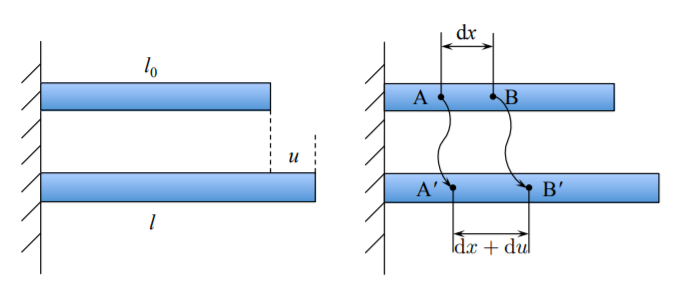
La cepa debe definirse localmente y no para toda la estructura. Considerar un elemento infinitesimal\(dx\) en la configuración no deformada, Figura\(\PageIndex{2}\). Después de la deformación, la longitud del elemento material original se vuelve\(dx + du\). La deformación de ingeniería es entonces
\[\epsilon_{\text{eng}} = \frac{(dx + du) − dx}{dx} = \frac{du}{dx} \label{1.1.7}\]
La derivada espacial del campo de desplazamiento se denomina gradiente de desplazamiento\(\boldsymbol{F} = \frac{du}{dx}\). Para el estado uniaxial la deformación es simplemente el gradiente de desplazamiento. Esto no es cierto para el caso general 3-D.
La cepa local de Cauchy se obtiene tomando valores relativos de la diferencia del cuadrado de las longitudes. Como se muestra en la Ecuación\ ref {1.1.5}, para que la cepa Cauchy se reduzca a la deformación de ingeniería, se debe introducir el factor 2 en la definición. Así
\[\epsilon_c = \frac{1}{2} \frac{(dx + du)^2 − dx^2}{dx^2} = \frac{du}{dx} + \frac{1}{2} \left( \frac{du}{dx} \right)^2\]
o\(\epsilon_c = \boldsymbol{F} + \frac{1}{2} \boldsymbol{F}^2\). Para gradientes de desplazamiento pequeños,
\[\epsilon_c = \epsilon_{\text{eng}}\]