1.2: Extensión al caso 3-D

Última actualización
Guardar como PDF

Page ID: 85206

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

La ecuación (1.1.7) se puede reescribir en una forma alternativa

\[ d u = \epsilon d x\]

Considera un espacio euclidiano y denota por\(\boldsymbol{x} = \{x_1, x_2, x_3\}\) o\(x_i\) el vector que representa una posición de un punto genérico de un cuerpo. En el caso general tridimensional, el desplazamiento del punto material es también un vector con componentes\(\boldsymbol{u} = \{u_1, u_2, u_3\}\) o\(u_i\) donde\(i = 1, 2, 3\). Recordemos que el incremento de una función de tres variables es una suma de tres componentes

\[ d u_1(x_1, x_2, x_3) = \frac{\partial u_1}{ \partial x_1} d x_1 + \frac{\partial u_1}{ \partial x_2} dx_2 + \frac{\partial u_1}{ \partial x_3} d x_3\]

En general, los componentes del vector de incremento de desplazamiento son

\[ du_i(x_i) = \frac{\partial u_i}{ \partial x_1} d x_1 + \frac{\partial u_i}{ \partial x_2} d x_2 + \frac{\partial u_i}{ \partial x_3} d x_3 = \sum_{j=1}^3 \frac{\partial u_i}{ \partial x_j} d x_j\]

donde el repetido\(j\) es el denominado índice “ficticio”. El gradiente de desplazamiento

\[\boldsymbol{F} = \frac{\partial u_i}{ \partial x_j}\]

no es un tensor simétrico. También contiene términos de rotación de cuerpo rígido. Esto se puede mostrar reescribiendo la expresión para\(\boldsymbol{F}\) en una forma equivalente

\[\frac{\partial u_i}{ \partial x_j} = \frac{1}{2} \left(\frac{\partial u_i}{ \partial x_j} + \frac{\partial u_j}{ \partial x_i}\right) + \left(\frac{1}{2}\frac{\partial u_i}{ \partial x_j} - \frac{\partial u_j}{ \partial x_i}\right) \label{1.2.5}\]

El tensor de deformación\(\epsilon_{ij}\) se define como una parte “simétrica” del gradiente de desplazamiento, que es el primer término en la Ecuación\ ref {1.2.5}.

\[\epsilon_{ij} = \frac{1}{2} \left(\frac{\partial u_i}{ \partial x_j} + \frac{\partial u_j}{ \partial x_i}\right) \label{1.2.6}\]

Ahora, intercambiar (transponer) los índices\(i\) y\(j\) en la Ecuación\ ref {1.2.6}:

\[\epsilon_{ji} = \frac{1}{2} \left(\frac{\partial u_j}{ \partial x_i} - \frac{\partial u_i}{ \partial x_j}\right) \label{1.2.7}\]

El primer término en la Ecuación\ ref {1.2.7} es el mismo que el segundo término en la Ecuación\ ref {1.2.6}. Y el segundo término en la Ecuación\ ref {1.2.7} es idéntico al primer término en la Ecuación\ ref {1.2.6}. Por lo tanto, el tensor de tensión es simétrico

\[\epsilon_{ij} = \epsilon_{ji}\]

El motivo para introducir las propiedades de simetría del tensor de deformación se explicará más adelante en esta sección. El segundo término en la Ecuación\ ref {1.2.5} se llama el tensor de espín\(\omega_{ij}\)

\[\omega_{ij} = \frac{1}{2} \left(\frac{\partial u_i}{ \partial x_j} + \frac{\partial u_j}{ \partial x_i}\right)\]

Usando argumentos similares a los anteriores es fácil ver que el tensor de giro es antisimétrico

\[w_{ij} = -w_{ji} \label{1.2.10}\]

De la definición se deduce que los términos diagonales del tensor de giro son cero, por ejemplo\(w_{11} = −w_{11} = 0\). Los componentes, del tensor de tensión son:

\(i = 1, j = 1\)\[ \epsilon_{11} = \frac{1}{2} \left(\frac{\partial u_1}{ \partial x_1} + \frac{\partial u_1}{ \partial x_1}\right) = \frac{\partial u_1}{ \partial x_1} \label{1.2.11}\]
\(i = 2, j = 2\)\[\epsilon_{22} = \frac{\partial u_2}{ \partial x_2}\]
\(i = 3, j = 3\)\[ \epsilon_{33} = \frac{\partial u_3}{ \partial x_3}\]
\(i = 1, j = 2\)\[\epsilon_{12} = \epsilon_{21} = \frac{1}{2} \left(\frac{\partial u_1}{ \partial x_2} + \frac{\partial u_2}{ \partial x_1}\right)\]
\(i = 2, j = 3\)\[ \epsilon_{23} = \epsilon_{32} = -\frac{1}{2} \left(\frac{\partial u_2}{ \partial x_3} + \frac{\partial u_3}{ \partial x_2}\right)\]
\(i = 3, j = 1\)\[ \epsilon_{31} = \epsilon_{13} = -\frac{1}{2} \left(\frac{\partial u_3}{ \partial x_1} + \frac{\partial u_1}{ \partial x_3}\right)\]

Para la interpretación geométrica del tensor de deformación y espín considere un elemento cuadrado infinitesimal\((dx_1, dx_2)\) sometido a varios casos simples de deformación. Las derivadas parciales son reemplazadas por diferencias finitas, por ejemplo

\[\frac{\partial u_1}{ \partial x_1} = \frac{\Delta u_1}{\Delta x_1} = \frac{u_1(x_1) - u_1(x_1 +h)}{h}\]

Traslación de cuerpo rígido

A lo largo\(x_1\) del eje:

\[u_1(x_1) = u_1(x_1 + h)\]

\[u_2 = u_3 = 0\]

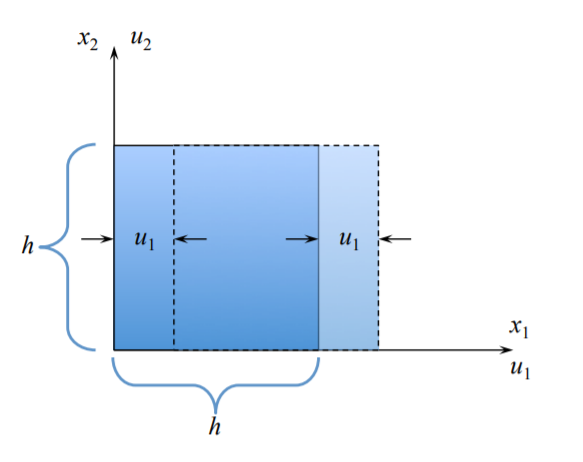
1.2.1.png — Figura\(\PageIndex{1}\): Traslación rígida del cuerpo del elemento cuadrado infinitesimal.

De\ ref {1.2.11} se deduce que el componente de deformación correspondiente se desvanece,\(\epsilon_{11} = 0\). El primer componente del tensor de espín es cero de la definición,\(\omega_{11} = 0\).

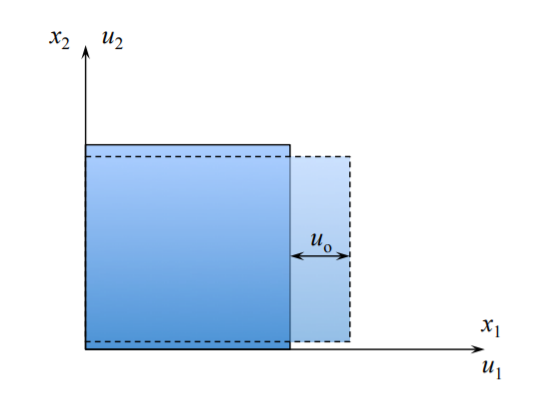
Extensión a lo largo\(x_1\) del eje

En\(x_1\):\(u_1 = 0\).

En\(x_1 + h\):\(u_1 = u_o\).

La cepa correspondiente es\(\epsilon_{11} = \frac{u_o}{h}\).

Cizalla pura en el\(x_1x_2\) plano

En\(x_1 = 0\) y\(x_2 = 0\):\(u_1 = u_2 = 0\)

En\(x_1 = h\) y\(x_2 = 0\):\(u_1 = 0\) y\(u_2 = u_o\)

En\(x_1 = 0\) y\(x_2 = h\):\(u_1 = u_o\) y\(u_2 = 0\)

1.2.2.png — Figura\(\PageIndex{2}\): El elemento cuadrado se estira en una dirección.

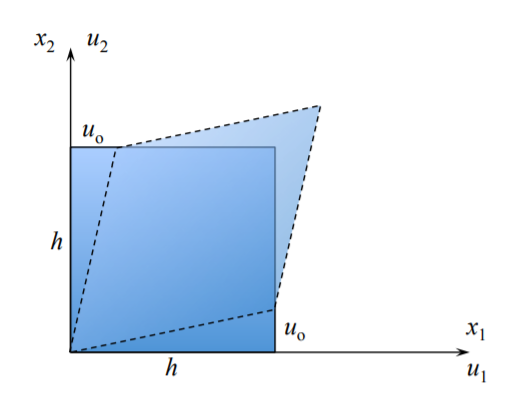
1.2.3.png — Figura\(\PageIndex{3}\): Imposición de gradientes deformativos constantes.

De la Ecuación\ ref {1.2.10} y de la Ecuación\ ref {1.2.6} se deduce que:

\[\epsilon_{12} = \frac{1}{2} \left( \frac{u_o}{h} +\frac{u_o}{h}\right) = \frac{u_o} {h}\]

\[\omega_{12} = \frac{1}{2} \left( \frac{u_o}{h} − \frac{u_o}{h}\right) = 0\]

La deformación resultante representa el cambio de ángulos del elemento rectilíneo inicial.

Rotación de cuerpo rígido

En\(x_1 = 0\) y\(x_2 = 0\):\(u_1 = u_2 = 0\)

En\(x_1 = h\) y\(x_2 = 0\):\(u_1 = 0\) y\(u_2 = u_o\)

En\(x_1 = 0\) y\(x_2 = h\):\(u_1 = -u_o\) y\(u_2 = 0\)

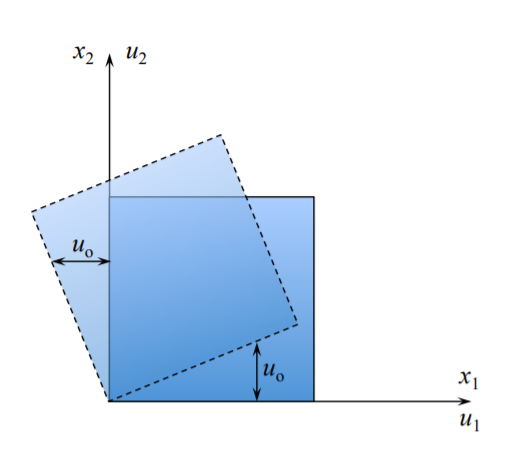
1.2.4.png — Figura\(\PageIndex{4}\): Elemento cuadrado infinitesimal sometido a rotación de cuerpo rígido.

Cambiar el signo de\(u_1\) at\(x_1 = 0\) y\(x_2 = h\) de\(u_o\) a\(-u_o\) da como resultado un giro distinto de cero pero una deformación cero

\[\epsilon_{12} = \frac{1}{2} \left( \frac{u_o}{h} + \left(− \frac{u_o}{h}\right)\right) = 0\]

\[\omega_{12} = \frac{1}{2} \left( \frac{u_o}{h} + \left(− \frac{u_o}{h}\right)\right) = \frac{u_o} {h}\]

El último ejemplo proporciona una explicación de por qué el tensor de deformación se definió como una parte simétrica del gradiente de desplazamiento. La física dicta que la traslación y rotación del cuerpo rígido no deben inducir ninguna tensión en el elemento material. En el cuerpo rígido los gradientes de desplazamiento de rotación no son cero. El tensor de deformación, definido como una parte simétrica del gradiente de desplazamiento elimina el efecto de rotación en el estado de deformación en un cuerpo. En otras palabras, la deformación describió el cambio de longitud y ángulos mientras que el giro, la rotación del elemento.