2.6: Tema Avanzado - Teoría Matemática de Vigas
- Page ID
- 85223
Las ecuaciones de equilibrio de una viga con sección transversal rectangular se pueden derivar de manera elegante a partir de la ecuación de equilibrio 3-D. Con fuerzas corporales cero, la ecuación de equilibrio en la notación de índice compacto es
\[ \sigma_{ij,j} = 0 \]
o la notación expandida
\[i = 1, \, \sigma_{1j,j} = 0 \rightarrow \sigma_{11,1} + \sigma_{12,2} + \sigma_{13,3} = 0\]
\[i = 2, \, \sigma_{2j,j} = 0 \rightarrow \sigma_{21,1} + \sigma_{22,2} + \sigma_{23,3} = 0\]
\[i = 3, \, \sigma_{3j,j} = 0 \rightarrow \sigma_{31,1} + \sigma_{32,2} + \sigma_{33,3} = 0\]
En la notación de ingeniería, el conjunto completo de ecuaciones de equilibrio, ya dado por Ecuaciones (2.1.26-2.1.28), es
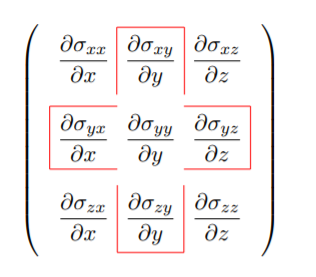\[\label{2.6.5}\]
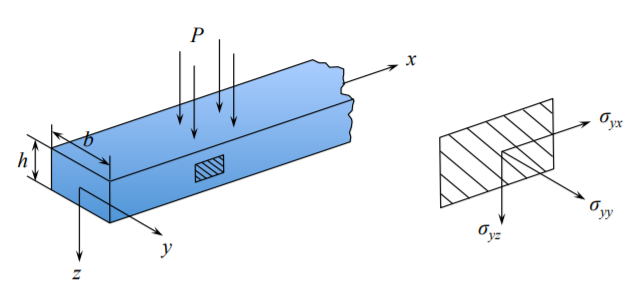
cuál de los componentes del tensor de tensión sobrevivirá a la suposición del haz. Considere una viga de sección transversal rectangular\((h \times b)\) sometida a flexión plana, Figura (\(\PageIndex{1}\)).
La viga se somete a carga de presión\(p\) en el plano\(z = − \frac{h}{2}\). En el caso de flexión plana no debe haber gradiente de tensiones en la\(y\) dirección -dirección. Por lo tanto el término\(\frac{\partial \sigma_{xy}}{\partial y} = 0\). Los componentes supervivientes se encuentran fuera de la caja sombreada en la Ecuación\ ref {2.6.5}, y son:
\[\frac{\partial \sigma_{xx}}{\partial x} + \frac{\partial \sigma_{xz}}{\partial z} = 0 \label{2.6.6}\]
\[\text{Equation in the y-direction is satisfied identically} \label{2.6.7}\]
\[\frac{\partial \sigma_{zx}}{\partial x} + \frac{\partial \sigma_{zz}}{\partial z} = 0 \label{2.6.8}\]
Condiciones de Límite
Las condiciones de contorno se especifican mediante la fórmula de Cauchy. Las superficies laterales así\(y = \pm \frac{b}{2}\) como la repisa inferior\(z = \frac{h}{2}\) están libres de estrés. Considera solo el estante superior\(z = −\frac{h}{2}\), definido por el vector normal unitario\(\boldsymbol{n}[0, 0, −1]\). Supongamos que no se aplica carga de cizallamiento, de manera que la carga distribuida se dirige a lo largo\(z\) del eje.
Los componentes de tracción superficial en la repisa superior son\(\boldsymbol{T}[0, 0, p]\). A partir de la fórmula de Cauchy, calcule el\(z\) -componente de la tracción superficial\( T_3 = \sigma_{3j}n_j = \sigma_{31}n_1 + \sigma_{32}n_2 + \sigma_{33}n_3 \). Sólo el último término, para el que\(n_3 = −1\) queda y así
\[T_3 = p = - \sigma_{33} = -\sigma_{zz}\]
Fue sencillo ver que la presión\(p\) debe ser equilibrada por el\(\sigma_{zz}\) componente. No obstante, para una determinación precisa del signo, la fórmula de Cauchy resultó ser útil. Todos los demás componentes del tensor de tensión en la superficie lateral de la viga son cero.
La derivación consta de tres pasos. La primera ecuación\ ref {2.6.6} se integra con respecto a\(z\) y se multiplica por el ancho del haz\(b\)
\[\int_{-\frac{h}{2}}^{\frac{h}{2}} \frac{\partial \sigma_{xx}}{\partial x} dz + b \int_{-\frac{h}{2}}^{\frac{h}{2}} \frac{\partial \sigma_{xz}}{\partial z} dz = 0\]
A continuación, para una integral definida, la diferenciación del integrante en la primera es equivalente a la diferenciación de la integral. El segundo término se puede integrar para dar
\[\int_{-\frac{h}{2}}^{\frac{h}{2}} \sigma_{xx}b dz + \sigma_{xz}|_{-\frac{h}{2}}^{\frac{h}{2}} = 0\]
Señalando que\(b dz = dA\), la primera integral representa la fuerza axial\(N\), según la definición, Ecuación\ ref {2.6.7}. El esfuerzo cortante\(\sigma_{xz}\) es distinto de cero dentro de la altura de la viga pero desaparece en los estantes inferior y superior,\(\sigma_{xz} = 0\), en\(z = \frac{h}{2}\) y\(z = − \frac{h}{2}\). Solo sobrevive el primer término, que es el equilibrio de fuerzas en la\(x\) dirección -dirección
\[\frac{dN}{dx} = 0 \text{ or } N^{\prime} = 0 \]
En el segundo paso ambos lados de la Ecuación\ ref {2.6.6} se multiplican por\(bz\) y se vuelven a integrar con respecto a\(z\)
\[\int_{-\frac{h}{2}}^{\frac{h}{2}} \frac{\partial \sigma_{xx}}{\partial x} z (b dz) + b \int_{-\frac{h}{2}}^{\frac{h}{2}} \frac{\partial \sigma_{xz}}{\partial z} z (bdz) = 0\]
El segundo término ahora está integrado por partes
\[\frac{d}{dx} \int_{-\frac{h}{2}}^{\frac{h}{2}} \sigma_{xx}z dA + \{\sigma_{xz}|_{-\frac{h}{2}}^{\frac{h}{2}} - \int_{-\frac{h}{2}}^{\frac{h}{2}} \sigma_{xz} dA\} = 0\]
El segundo término se desvanece, como antes. La primera integral es el momento de flexión\(M\) mientras que la segunda es la fuerza cortante\(V\) (ver las definiciones, Ecuaciones\ ref {2.6.6} -\ ref {2.6.8}. Entonces, la ecuación anterior representa el equilibrio de momento
\[\frac{dM}{dx} − V = 0 \label{2.6.15}\]
En el tercer paso final, la Ecuación\ ref {2.6.15} se integra con respecto a\(z\) después de ser multiplicada por\(b\).
\[\int_{-\frac{h}{2}}^{\frac{h}{2}} \frac{\partial \sigma_{xz}}{\partial x} (b dz) + \int_{-\frac{h}{2}}^{\frac{h}{2}} \frac{\partial \sigma_{zz}}{\partial z} (bdz) = 0\]
Después de la integración se obtiene
\[\frac{d}{dx} \int_{-\frac{h}{2}}^{\frac{h}{2}} \sigma_{xz} dA + b \left[\sigma_{zz}|_{\frac{h}{2}} - \sigma_{zz}|_{-\frac{h}{2}}\right] = 0 \label{2.6.17}\]
Recordando la condición de contorno\(\sigma_{zz}|_{\frac{h}{2}}\) y\(\sigma_{zz}|_{\frac{h}{2}} = −p\), Ecuación\ ref {2.6.17} rendimientos
\[\frac{dV}{dx} + b(−1)(−p) = 0\]
o usando\(bp = q\)
\[\frac{dV}{dx} + q = 0 \label{2.6.19}\]
Eliminando la fuerza cortante entre la Ecuación\ ref {2.6.15} y la Ecuación\ ref {2.6.19}, se obtiene la ecuación de equilibrio del haz.
\[\frac{d^2M}{dx^2} + q(x) = 0\]
Esta ecuación es idéntica a la derivada del principio del trabajo virtual.