3.2: Ley de Elasticidad en Continuum 3-D
- Page ID
- 85111
La segunda pregunta es cómo extender la Ecuación (3.1.1) al estado general 3-D. Tanto la tensión como la deformación son tensores por lo que se debe buscar la relación entre ellos como una transformación lineal en la forma
\[\sigma_{ij} = C_{ij,kl} \epsilon_{kl}\]
donde\(C_{ij,kl}\) está la matriz con\(9 \times 9 = 81\) coeficientes. Usando las propiedades de simetría del tensor de tensión y deformación y la suposición de isotropía material, el número de constantes independientes se reduce de 81 a solo dos. Estas constantes, llamadas constantes Lame', se denotan por\ ((\ chi,\ mu). La relación general de esfuerzo y deformación para un material elástico lineal es
\[\sigma_{ij} = 2\mu\epsilon_{ij} + \lambda \epsilon_{kk} \delta_{ij} \label{3.2.2}\]
donde\(\delta_{ij}\) está la matriz de identidad, o Kronecker “\(\delta\)”, definida por
\ [\ delta_ {ij} =\ begin {vmatrix}
1 & 0 & 0\\
0 & 1 & 0\\ 0 & 0 & 1
\ end {vmatrix}\ text {o}\ begin {array}\ delta_ {ij} = 1\;\ text {if} i = j\\\ delta_ {ij} = 0\ texto {if} i\ neq\ end {array}\]
y\(\epsilon_{kk}\) es, de acuerdo con la convención de suma,
\[\epsilon_{kk} = \epsilon_{11} + \epsilon_{22} + \epsilon_{33} = \frac{dV}{V}\]
En la forma expandida, la Ecuación\ ref {3.2.2} dice
\[\sigma_{11} = 2\mu \epsilon_{11} + \lambda(\epsilon_{11} + \epsilon_{22} + \epsilon_{33}), \quad \quad \delta_{11} = 1 \label{3.2.5}\]
\[\sigma_{22} = 2\mu \epsilon_{22} + \lambda(\epsilon_{11} + \epsilon_{22} + \epsilon_{33}), \quad \quad \delta_{22} = 1\]
\[\sigma_{33} = 2\mu \epsilon_{33} + \lambda(\epsilon_{11} + \epsilon_{22} + \epsilon_{33}), \quad \quad \delta_{33} = 1\]
\[\sigma_{12} = 2\mu \epsilon_{12} \quad \quad \delta_{12} = 0\]
\[\sigma_{23} = 2\mu \epsilon_{23} \quad \quad \delta_{23} = 0\]
\[\sigma_{31} = 2\mu \epsilon_{31} \quad \quad \delta_{31} = 0 \label{3.2.10}\]
Nuestra tarea es expresar las constantes de Lame' mediante un par de constantes de ingeniería (\(E(\nu)\), donde\(\nu\) está la relación de Poisson). Para ello, utilizamos el experimento virtual de tensión de una barra rectangular
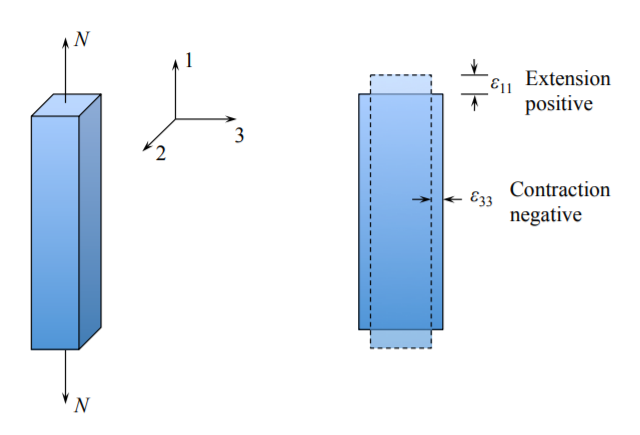
En la prueba conceptual, se miden la fuerza, el desplazamiento y el cambio en la dimensión transversal. Las observaciones experimentales se pueden resumir de la siguiente manera:
- \(\sigma_{11}\)es proporcional a\(\epsilon_{11}, \sigma_{11} = E\epsilon_{11}\)
- \(\epsilon_{22}\)es proporcional a\(\epsilon_{11}, \epsilon_{22} = -\nu\epsilon_{11}\)
- \(\epsilon_{33}\)es proporcional a\(\epsilon_{11}, \epsilon_{33} = -\nu\epsilon_{11}\)
Así, la tensión uniaxial está produciendo el estado unidimensional de tensión pero el estado tridimensional de tensión
\ [\ sigma_ {ij} =\ begin {vmatrix}
\ sigma_ {11} & 0 & 0\\
0 & 0 & 0\\ 0 & 0 & 0
\ end {vmatrix}\;\ epsilon_ {ij} =\ begin {vmatrix}
\ epsilon_ {11} & 0 & 0\\
0 &\ epsilon_ {22} & 0\ 0 & 0 &\ epsilon_ {33}
\ end {vmatrix}\]
Introducimos ahora la información anterior en Ecuaciones\ ref {3.2.5} -\ ref {3.2.10}.
\[\sigma_{11} = 2\mu \epsilon_{11} + \chi(\epsilon_{11} - \nu \epsilon_{11} - \nu\epsilon_{11}) = E\epsilon_{11}\]
\[\sigma_{22} = 2\mu (-\nu\epsilon_{11}) + \chi(\epsilon_{11} - \nu\epsilon_{11} - \nu \epsilon_{11}) = 0\]
y obtener dos ecuaciones lineales relacionadas\((\chi, \mu)\) con\((E, \nu)\)
\[2\mu + \chi(1 − 2\nu) = E \label{3.2.14}\]
\[-2\mu\nu + \chi(1 − 2\nu) = 0 \label{3.2.15}\]
Resolviendo Ecuaciones\ ref {3.2.14} -\ ref {3.2.15} para\(\mu\) y\(\chi\) da
\[\mu = \frac{E}{2(1 − \nu)}\]
\[\chi = \frac{E\nu}{(1 + \nu)(1 − 2\nu)}\]
La ley general de elasticidad 3-D, expresada en términos\((E, \nu)\) de
\[\sigma_{ij} = \frac{E}{1 + \nu} \left[ \epsilon_{ij} + \frac{\nu}{1-2\nu}\epsilon_{kk}\delta_{ij}\right] \label{3.2.18}\]
El estrés medio\(p\) donde\(−p = \frac{1}{3}\sigma_{kk} = \frac{1}{3} (\sigma_{11} + \sigma_{22} + \sigma_{33})\) se llama la presión hidrostática. Al mismo tiempo, la suma de los componentes diagonales del tensor de deformación denota el cambio de volumen. Hagamos la llamada “contracción” del tensor de tensión en la Ecuación\ ref {3.2.18}, lo que significa que\(i = j = k\)
\[\sigma_{kk} = \frac{E}{1 + \nu} \left[ \epsilon_{kk} + \frac{\nu}{1-2\nu}\epsilon_{kk}\cdot 3\right] \]
donde\(\delta_{kk} = (\delta_{11} + \delta_{22} + \delta_{33}) = 1 + 1 + 1 = 3\). De las ecuaciones anteriores se obtiene la siguiente relación entre la presión hidrostática y el cambio de volumen
\[−p = \kappa\frac{dV}{V}\]
donde\(\kappa\) esta el modulo de masa
\[\kappa = \frac{E}{3(1 − 2\nu)}\]
El material elástico es claramente compresible. Es la celosía cristalina la que se comprime pero al retirarla las fuerzas vuelven al volumen original.
La forma invertida de la ley del gancho 3-D es
\[\epsilon_{ij} = \frac{1 + \nu}{E} \sigma_{ij} − \frac{\nu}{E}\sigma_{kk}\delta_{ij}\]
que en términos de los componentes rinde
\[\epsilon_{11} = \frac{1}{E}[\sigma_{11} − \nu(\sigma_{22} + \sigma_{33})] \label{3.2.23}\]
\[\epsilon_{22} = \frac{1}{E}[\sigma_{22} − \nu(\sigma_{11} + \sigma_{33})]\]
\[\epsilon_{33} = \frac{1}{E}[\sigma_{33} − \nu(\sigma_{11} + \sigma_{22})]\]
\[\epsilon_{12} = \frac{1}{2\epsilon}\sigma_{12}\]
\[\epsilon_{23} = \frac{1}{2\epsilon}\sigma_{23}\]
\[\epsilon_{31} = \frac{1}{2\epsilon}\sigma_{31} \label{3.2.28}\]
donde\(G = \frac{E}{2(1 + \nu)}\) se llama el módulo de cizallamiento. Ecuaciones\ ref {3.2.23} -\ ref {3.2.28} ilustra el acoplamiento de cepas directas individuales con todos los componentes directos (diagonales) del tensor de tensión. Al mismo tiempo no hay acoplamiento en respuesta al cizallamiento. La deformación cortante es proporcional al esfuerzo cortante correspondiente.


