3.3: Especificación para el Continuum 2-D

Estrés Plano

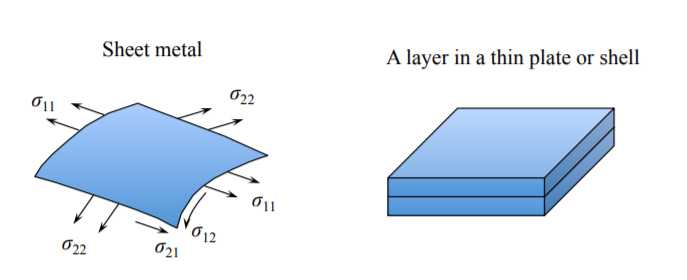
Este es el estado de estrés que se desarrolla en placas delgadas y conchas por lo que requiere una cuidadosa consideración. El estado de tensión en el cual\(\sigma_{3j} = 0\), donde el\(x_3 = z\) eje está en la dirección del espesor pasante. Los componentes distintos de cero del tensor de tensión son:

\ [\ sigma_ {ij} =\ begin {vmatrix}
\ sigma_ {11} &\ sigma_ {12} & 0\
\ sigma_ {21} &\ sigma_ {22} & 0\\ 0 & 0
\ end {vmatrix}\;\ epsilon_ {ij} =\ begin {vmatrix}
\ epsilon_ {11} &\ épsilon_ {12} & 0\\
\ épsilon_ {21} &\ epsilon_ {22} & 0\\ 0 &\ epsilon_ {33}
\ end {vmatrix}\]

dónde\(i, j = 1, 2, 3\) y\(\alpha, \beta = 1, 2\). En consecuencia,\(\sigma_{kk} = \sigma_{11} + \sigma_{22} + \sigma_{33} = \sigma_{\gamma\gamma} + 0\). La ley de elasticidad 2-D toma la siguiente forma en la notación tensora

\[\epsilon_{\alpha \beta} = \frac{1 + \nu}{E} \sigma_{\alpha \beta} − \frac{\nu}{E} \sigma_{\gamma\gamma} \delta_{\alpha \beta} \label{3.3.2}\]

Se puede verificar fácilmente desde la Ecuación\ ref {3.3.2} que en tensión plana\(\epsilon_{13} = \epsilon_{23} = 0\) pero\(\epsilon_{33} = − \frac{\nu}{E} (\sigma_{11}+\sigma_{22})\). El componente de espesor pasante del tensor de tensión no es cero. Debido a que no entra en la relación tensión-desplazamiento plano, su presencia no contribuye a las soluciones. Sólo se puede determinar posteriormente a partir de las tensiones conocidas\(\sigma_{11}\) y\(\sigma_{22}\).

Al hacer contracción\(\epsilon_{kk} = \frac{1 − \nu} {E} \sigma_{kk}\), uno puede invertir fácilmente la ecuación\ ref {3.3.2} en la forma

\[\sigma_{\alpha \beta} = \frac{E}{1 + {\nu}^2} [(1-\nu)\epsilon_{\alpha \beta} + \nu \epsilon_{\gamma\gamma} \delta_{\alpha \beta}] \]

La ecuación anterior es un punto de partida para derivar la ley de elasticidad en cantidades generalizadas para placas y conchas. Volveremos a esa tarea más adelante en esta conferencia. Antes de eso, discutamos otros tres casos limitantes importantes

\[\sigma_{11} = \frac{E}{1 - {\nu}^2}(\epsilon_{11} + \nu\epsilon_{22})\]

\[\sigma_{22} = \frac{E}{1 - {\nu}^2} (\epsilon_{22} + \nu\epsilon_{11})\]

\[\sigma_{13} = \frac{E}{1 + {\nu}} \epsilon_{12} \]

Figura\(\PageIndex{1}\): Ejemplos de estructuras de tensión plana.

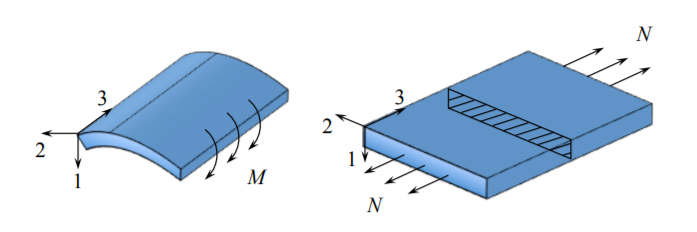
La deformación del plano se mantiene cuando sea\(\epsilon_{2j} = 0\). Al imponer una restricción a\(\epsilon_{22} = 0\), inmediatamente se desarrolla una reacción en la dirección como\(\sigma_{22} \neq = 0\).

Los componentes de los tensores de tensión y ecuaciones (3.2.12-3.2.13) son

\ [\ epsilon_ {ij} =\ begin {vmatrix}
\ epsilon_ {11} &\ epsilon_ {12} & 0\\
\ epsilon_ {21} &\ epsilon_ {22} & 0\\ 0 & 0 & 0
\ end {vmatrix}\;\ sigma_ {ij} =\ begin {vmatrix}
\ sigma_ {11} &\ sigma_ {12} & 0\\
\ sigma_ { 21} &\ sigma_ {22} & 0\\ 0 &\ sigma_ {33}
\ end {vmatrix}\]

¿Se puede demostrar que bajo el supuesto de la deformación del avión, la tensión de reacción\(\sigma_{33} = \nu(\sigma_{11} + \sigma_{22})\)? La deformación plana se encuentra en muchas situaciones prácticas, como la flexión cilíndrica de una placa o una viga ancha.

Figura\(\PageIndex{2}\): La tensión de flexión de una hoja/placa ancha da lugar a una deformación plana.

Tensión uniaxial

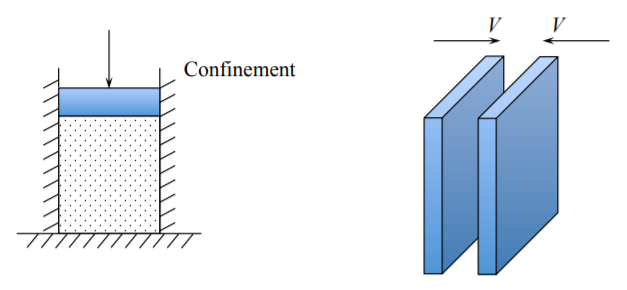
La deformación uniaxial se logra cuando se constriñe el desplazamiento en dos direcciones. Por ejemplo, el suelo o materiales granulares se prueban en un cilindro (llamado confinamiento) con un pistón, Figura (\(\PageIndex{3}\)). La deformación uniaxial también se desarrolla en una capa comprimida entre dos placas rígidas. También el impacto de placa a placa de alta velocidad produce la deformación unidimensional. Aquí el único componente del tensor de tensión es la tensión volumétrica. Los experimentos placa a placa se llevan a cabo para establecer la compresibilidad no lineal de metales bajo carga hidrostática muy alta\(\sigma_{kk} = −3p\). De manera similar, la onda plana en el espacio 3-D está generando una tensión uniaxial.

Figura\(\PageIndex{3}\): Ejemplos de problemas en los que el estado de deformación es uniaxial.

Los componentes del tensor de tensión y deformación en la deformación uniaxial son:

\ [\ sigma_ {ij} =\ begin {vmatrix}
\ sigma_ {11} &\ sigma_ {12} & 0\\ sigma_ {21} &
\ sigma_ {22} & 0\\ sigma_ {33}\ end {vmatrix}\;
\ epsilon_ {ij} =\ begin {vmatrix}\ epsilon_ {ij} =\ begin {vmatrix}
\ epsilon_ _ {11} & 0 &
0\\ 0 & 0\\ 0 & 0 & 0
\ end {vmatrix}\]

Donde las tensiones de reacción están relacionadas con la tensión activa\(\sigma_{11}\) por\(\sigma_{22} = \sigma_{33} = \frac{\nu(1 + \nu)\sigma_{11}}{1 − \nu^2}\). ¿Puedes probarlo?

El estado de tensión uniaxial se discutió anteriormente en esta conferencia al convertir las constantes Lame' en constantes de ingeniería\((E, \nu)\).