3.4: Ley de Hook en Cantidades Generalizadas para Vigas

Hay tres fuerzas generalizadas en haces\((M, N, \nu)\) pero sólo dos cantidades cinemáticas generalizadas\((\epsilon^{\circ}, \kappa)\). No existe un desplazamiento generalizado sobre el cual la fuerza cortante pueda ejercer trabajo. Por lo que la fuerza cortante es tratada como una reacción en la teoría del haz elemental. Esto da lugar a cierta inconsistencia interna en la teoría del haz, que se enumerará en una sección separada.

El punto de partida en la derivación de la ley de elasticidad para vigas es la hipótesis de Euler-Bernoulli,

\[\epsilon(z) = \epsilon^{\circ} + z\kappa\]

y la ley de gancho unidimensional, Ecuación (3.1.1), y la definición del momento de flexión y la fuerza axial en la viga, Ecuaciones (2.2.16-2.2.18). Calculemos primero la fuerza axial\(N\)

\[N = \int_{A} \sigma_{xx} dA = \int_{A} E \epsilon_{xx}dA = E\int_{A} (\epsilon^{\circ} + z\kappa) dA \\ = E \int_{A} \epsilon^{\circ} dA + E \int_{A} \kappa z dA = E\epsilon^{\circ} \int_{A} dA + E\kappa \int_{A} z dA\]

Tenga en cuenta que la deformación del eje medio\(\epsilon^{\circ}\) y la curvatura del eje del haz son independientes\(z\) de la coordenada y podrían llevarse frente a las integrales respectivas. También\(Q = \int_{A} zdA\) es el momento estático (primer) de inercia de la sección transversal. A partir de la definición del eje neutro,\(Q = 0\). La expresión de la fuerza axial se reduce entonces a

\[N = EA\epsilon^{\circ}\]

donde\(EA\) se llama la rigidez axial de la viga. Calculamos a continuación el momento de flexión de manera similar

\[N = \int_{A} \sigma_{xx}z dA = \int_{A} E(\epsilon^{\circ} + z\kappa)z dA \\ = E\epsilon^{\circ} \int_{A} z dA + E\kappa \int_{A} z^2 dA\]

Porque el primer término que involucra el momento estático de inercia se desvanece, y la expresión para el momento de flexión se vuelve

\[M = EI\kappa\]

donde EI se llama rigidez a la flexión y

\[I = \int_{A} z^2 dA\]

es el segundo momento de inercia. Para la sección transversal rectangular\((b \times h)\)

\[I = \frac{bh^3}{12}\]

La significancia de la derivación anterior es que la respuesta a la flexión está desacoplada de la respuesta axial y viceversa. Esta propiedad permite derivar la famosa fórmula de estrés para vigas. Esta es, de hecho, una derivación de línea

\[\sigma = E\epsilon = E(\epsilon^{\circ} + z\kappa) = E \left(\frac{N}{EA} + \frac{Mz}{EI}\right) \\ \sigma(z) = \frac{N}{A} + \frac{Mz}{I} \label{4.30}\]

Figura\(\PageIndex{1}\): Distribución lineal de tensiones a lo largo de la altura de la viga.

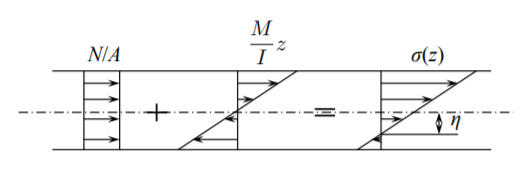
Tanto la fuerza axial como el momento de flexión contribuyen a la distribución de esfuerzos a lo largo de la altura de la viga, como se ilustra en la Figura (\(\PageIndex{1}\)).

A partir de la ecuación\ ref {4.30} se puede calcular el punto\(z = \eta\) donde las tensiones se vuelven cero

\[\eta = − \frac{I}{A}\frac{N}{M} = −\rho^2 \frac{N}{M}\]

donde\(\rho\) es el momento de la giración de la sección transversal definida por\(I = \rho^2A\). La posición del eje de tensión cero depende de la relación entre la fuerza axial y el momento de flexión. Si\(\eta < h\), donde\(h\) está el grosor de una viga de sección rectangular, el punto de tensión cero está dentro del límite de la viga, hay una respuesta dominada por flexión. La respuesta dominada por tensión es cuando\(\eta\) es varias veces mayor que\(h\).