3.5: Inconsistencias en la teoría del haz elemental
- Page ID
- 85117
Las ecuaciones presentadas en la Sección 2.6 bajo el TEMA AVANZADO se derivaron sin ningún supuesto aproximado. Para que la viga esté en equilibrio, la fuerza de corte\(V\) debe estar presente, cuando la viga está bajo flexión pura (flexión uniforme sobre la longitud de la viga). Es el esfuerzo cortante el\(\sigma_{xz}\) que da lugar a la fuerza cortante, según la definición, Ecuaciones (2.4.8-2.4.10). Por lo tanto, cualquier inconsistencia debe provenir de las relaciones deformación-desplazamiento así como de las ecuaciones constitutivas, donde se introdujeron algunas aproximaciones.
La presencia de esfuerzos cortantes\(\sigma_{xz} = \sigma_{13}\) significa que las deformaciones de cizallamiento\(\epsilon_{13} = \epsilon_{xz}\) deben desarrollarse de acuerdo con la Ecuación (4.16).
\[\epsilon_{xz}(z) = \frac{\sigma_{xz}(z)}{2G} \label{4.32}\]
La deformación por cizallamiento se define como
\[\epsilon_{xz} = \frac{1}{2} \left( \frac{\partial u_x}{\partial z} + \frac{\partial u_z}{\partial x}\right)\]
El supuesto de Euler-Bernoulli nos dice que la deformación por cizallamiento se desvanece. Entonces, se viola la Ecuación\ ref {4.32} porque la LH es cero mientras que la RH no lo es. Supongamos por un tiempo eso\(\epsilon_{xz} = 0\). Entonces
\[\frac{\partial u_x}{\partial z}= -\frac{\partial w(x)}{\partial x} = -\theta (x) \label{4.34}\]
donde\(u_z = w(x)\) es independiente de la coordenada\(z\). Integrando Ecuación\ ref {4.34} uno obtiene
\[u_x(z) = u^{\circ} − z \theta\]
que es equivalente a la hipótesis plano-restar-plano y normal-permanecer-normal, introducida en el Capítulo 1. Supongamos ahora que la deformación fuera del plano es una determinada función dada de\(z\). Al realizar la integración de la ecuación\ ref {4.32} de manera similar a la anterior, se obtiene
\[u_x(z) = u^{\circ} − z \theta + \int \epsilon_{xz}(z) dz \label{4.36}\]
De los resultados anteriores se desprende que la sección deformada no es plana sino que se deforma. La cantidad de deformación viene dada por el tercer término en la Ecuación\ ref {4.36}.
¿Podemos estimar la cantidad de urdimbre? Sí, pero tenemos que ir por delante del material presentado y cupar la solución para la pendiente desviada\(\theta\) de la viga. Le se asienta en el caso más simple de una viga en voladizo sujeta cargada en su punta por la fuerza puntual\(P\)
\[\theta = \frac{Pl^2}{2EI}\]
Esta solución se derivará en el Capítulo 4.
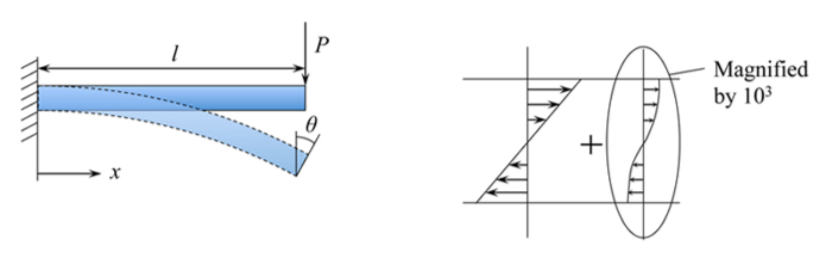
Otro resultado necesario es la distribución de esfuerzos cortantes a través de la altura de la viga. Para la viga de sección rectangular\((b \times h)\), el esfuerzo cortante es una función parabólica de\(z\)
\[\sigma_{xz}(z) = \frac{3}{2} \frac{P}{A} \left[1 − \frac{z^2}{(h/2)^2} \right] \]
La deformación correspondiente se calcula a partir de la Ecuación\ ref {4.32}. Supongamos que no hay fuerza axial,\(N = 0\), entonces a partir de la Ecuación (3.4.3)\(\epsilon^{\circ} = 0\) y\(u^{\circ} = 0\). Después de la integración, el perfil de desplazamiento definido por la ecuación\ ref {4.36} se convierte
\[u_{x}(z) = -\frac{Pl^2}{2EI}z + \frac{1}{2\epsilon} \frac{3}{2} \frac{P}{A} \left[z − \frac{z^3}{3(h/2)^2} \right] \]
Para cuantificar la corrección del campo de desplazamiento por deformación, calculemos los valores máximos de los dos términos en\(z = − \frac{h}{2}\). El primer término derivado del supuesto de EulerberNoulli da
\[u^{\mathrm{I}}_{x} (z = − \frac{h}{2}) = \frac{\rho l^2}{2EI} \frac{h}{2}\]
El segundo término de corrección es
\[u^{\mathrm{II}}_{x} (z = − \frac{h}{2}) = \frac{1}{2G} \frac{P}{A} \frac{h}{2}\]
La relación de los dos términos es
\[\left|\frac{u^{\mathrm{II}}_{x}}{u^{\mathrm{I}}_{x}} \right| = \frac{E}{2G} \frac{I}{Al^2} = \frac{E}{2G} (\frac{\rho}{l})^2 \label{4.42}\]
donde\(\rho\) está el radio de giro de la sección transversal. Para una sección transversal rectangular\((b \times h)\),
\[\rho^2 = \frac{I}{A} = \frac{bh^3}{12bh} = \frac{h^2}{12}\]
La relación\(E/2G\) es
\[\frac{E}{2G} = \frac{E}{2\frac{E}{2(1 + \nu)}} = (1 + \nu)\]
Entonces, la amplitud relativa de la deformación de la Ecuación\ ref {4.42} es
\[\left|\frac{u^{\mathrm{II}}_{x}}{u^{\mathrm{I}}_{x}} \right| = \frac{ (1 + \nu)}{12} \left(\frac{h}{l}\right)^2\]
Para una viga típica con\(\frac{l}{h} = 20\), la relación anterior se convierte\(0.25 \times 10^{−3}\)!!! Para comparar el plano y la sección transversal envuelta, la cantidad de urdimbre tuvo que ampliarse mil veces, ver Figura (\(\PageIndex{1}\)). Se puede concluir que el efecto de la deformación es de un orden\(0.1 %\) y se puede descuidar con seguridad en la teoría del haz de ingeniería. En otras palabras, la “rienda” del supuesto de Euler-Bernoulli es incuestionado.
Otra inconsistencia de la teoría del haz elemental es que la tensión uniaxial da lugar al estado de deformación triaxial. En particular, a partir de la ecuación constitutiva 3-D, los componentes de deformación
\[\epsilon_{yy} = \epsilon_{zz} = − \frac{\nu}{E}\sigma_{xx}\]
Tomemos como ejemplo la misma viga voladiza con carga de punta. El momento de flexión en la raíz de la viga es\(M = Pl\), y a partir de la fórmula de estrés,
\[\sigma_{xx} = \frac{Pl}{I} z\]
A partir de la definición\(\epsilon_{yy} = \frac{du_y}{dy}\), y después de integrarse con respecto a\(y\), se obtiene
\[u_y = − \frac{Pl\nu}{IE} zy\]
El desplazamiento máximo ocurre en\(z = \frac{h}{2}\) y\(y = \frac{b}{2}\). Haciendo uso de la fórmula de deflexión del haz (ver Capítulo 4)
\[\delta = \frac{Pl^3}{3EI} \text{ or } \frac{Pl}{EI} = \frac{3\delta}{l^2} \label{4.49}\]
la fórmula para el desplazamiento máximo de una viga, normalizada con respecto al grosor de la viga se convierte en
\[\frac{(u_y)_{max}}{h} = \frac{3}{4} \nu \left( \frac{\delta}{h}\right) \left( \frac{h}{l}\right)^2 \label{4.50}\]
¿Cuál es el rango de las desviaciones normalizadas del haz\(\delta\)? El haz se desvía elásticamente hasta que las fibras más estresadas alcanzan rendimiento de los materiales,\(\left. \sigma_{xx} \right|_{z= \frac{h}{2}} = \sigma_y\).
Luego, a partir de la fórmula del estrés
\[\sigma_{y} = \frac{Pl}{I} \frac{h}{2}\]
Combinando la expresión anterior con la fórmula de deflexión del haz, Ecuación\ ref {4.49}, la estimación para el desplazamiento máximo de la punta elástica
\[\frac{\delta}{h} = \frac{2}{3} \frac{\sigma_y}{E} \left( \frac{l}{h}\right)^2 \label{4.52}\]
Combinando Ecuaciones\ ref {4.50} y\ ref {4.52}, la expresión para el desplazamiento máximo normalizado de la esquina de la sección transversal se convierte
\[\frac{(u_y)_{max}}{h} = \frac{\nu}{2} \frac{\delta_y}{E}\]
Con valores realistas\(\nu = \frac{1}{3}\) y\(\frac{\sigma_y}{E} = 10^{−3}\), la cantidad de cambio máximo del ancho de la viga es\(0.1 %\) de la altura de la viga. Un cambio tan pequeño en la dimensión de la sección transversal no tiene ningún efecto práctico sobre la solución del haz. Se puede realizar un análisis similar para estimar el cambio en la altura de la viga.
Cuando se toman debidamente en cuenta los signos\(z\) y\(y\) coordenadas, los cálculos actuales predicen el siguiente cambio en la forma de la sección transversal.
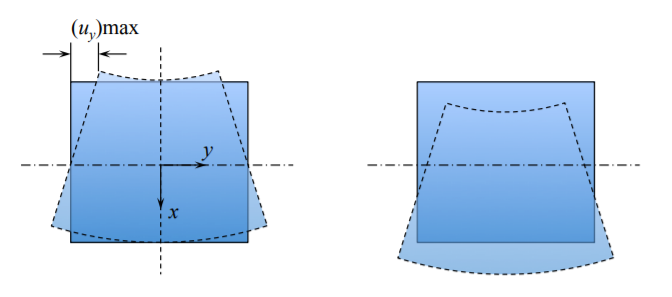
La deformación anticlástica se puede ver fácilmente doblando una goma de borrar, que es una viga muy corta. Podemos concluir en la presente sección que las inconsistencias internas de la teoría del haz no producen ningún error significativo en las aplicaciones de ingeniería. Por lo tanto, se puede asumir con seguridad que la sección transversal de la viga no se deforma y solo se mueve como un cuerpo rígido con las crecientes deflexiones de la viga.


