3.6: Derivación de Ecuaciones Constitutivas para Placas (Avanzada)

Para mayor comodidad, a continuación se resume el conjunto de ecuaciones necesarias para derivar la ley de elasticidad de las placas.

La ley de Hook en el estrés plano dice:

\[\sigma_{\alpha \beta} = \frac{E}{1 − \nu^2} [(1 − \nu)\epsilon_{\alpha \beta} + \nu\epsilon_{\gamma \gamma}\delta_{\alpha \beta}] \label{4.54} \]

En términos de componentes:

\[\sigma_{xx} = \frac{E}{1 − \nu^2}(\epsilon_{xx} + \nu\epsilon_{yy})\]

\[\sigma_{yy} = \frac{E}{1 − \nu^2}(\epsilon_{yy} + \nu\epsilon_{xx})\]

\[\sigma_{xy} = \frac{E}{1 − \nu} \epsilon_{xy}\]

Aquí, el tensor de deformación se puede obtener a partir de las relaciones deformación-desplazamiento:

\[\epsilon_{\alpha \beta} = \epsilon_{\alpha \beta}^{\circ} + z\kappa_{\alpha \beta}\]

Ahora, defina el tensor del momento de flexión:

\[M_{\alpha \beta} \equiv \int_{-\frac{h}{2}}^{\frac{h}{2}} \sigma_{\alpha \beta}z dz \label{4.57}\]

y el tensor de la fuerza axial (fuerza de membrana):

\[N_{\alpha \beta} \equiv \int_{-\frac{h}{2}}^{\frac{h}{2}} \sigma_{\alpha \beta}z dz\]

Momentos de flexión y energía de flexión

El momento de flexión ahora\(M_{\alpha \beta}\) se calcula sustituyendo la Ecuación\ ref {4.54} por la Ecuación\ ref {4.57}

\[M_{\alpha \beta} = \frac{E}{1 − \nu^2} \int_{-\frac{h}{2}}^{\frac{h}{2}} [(1 − \nu)\epsilon_{\alpha \beta} + \nu\epsilon_{\gamma \gamma}\delta_{\alpha \beta}] z dz \\ = \frac{E}{1 − \nu^2} [(1 − \nu)\epsilon_{\alpha \beta}^{\circ} + \nu\epsilon_{\gamma \gamma}^{\circ}\delta_{\alpha \beta}] \int_{-\frac{h}{2}}^{\frac{h}{2}} z dz \\ + \frac{E}{1 − \nu^2} [(1 − \nu)\kappa_{\alpha \beta} + \nu\kappa_{\gamma \gamma}\delta_{\alpha \beta}] \int_{-\frac{h}{2}}^{\frac{h}{2}} z^2 dz \\ = \frac{Eh^3}{12(1 − \nu^2)} [(1 − \nu)\kappa_{\alpha \beta} + \nu\kappa_{\gamma \gamma}\delta_{\alpha \beta}]\]

Obsérvese que el término\(\int_{-\frac{h}{2}}^{\frac{h}{2}} z dz \) es cero, como se muestra en el caso de las vigas. Por lo tanto, no hay deformaciones de superficie media\(\epsilon_{\alpha \beta}^{\circ}\) que entren en la relación momento-curvatura.

Aquí definimos la rigidez a la flexión de una placa de la\(D\) siguiente manera:

\[D = \frac{Eh^3}{12(1 − \nu^2)}\]

Ahora, se obtienen las relaciones momento-curvatura en la forma tensorial

\[\boxed{ M_{\alpha \beta} = D[(1 − \nu)\kappa_{\alpha \beta} + \nu\kappa_{\gamma \gamma}\delta_{\alpha \beta}] }\label{4.61}\]

\[M_{\alpha \beta} = \begin{vmatrix} M_{11} & M_{22} \\ M_{21} & M_{22} \end{vmatrix}\]

donde\(M_{12} = M_{21}\) debido a la simetría. En la notación ampliada,

\[M_{11} = D(\kappa_{11} + \nu\kappa_{22})\]

\[M_{22} = D(\kappa_{22} + \nu\kappa_{11})\]

\[M_{12} = D(1 - \nu)\kappa_{12})\]

Densidad de energía de flexión unidimensional

Aquí, usamos la notación hat para una función de cierto argumento, como:

\[M_{11} = \hat{M}_{11}(\kappa_{11}) \\ = D\kappa_{11}\]

Entonces, la densidad de energía de flexión\(\tilde U_b \) dice:

\[\bar U_b = \int_{0}^{\bar{\kappa}} \hat{M}_{11}(\kappa_{11}) d\kappa_{11} \\ = D \int^{\bar{\kappa}_{11}} \kappa_{11} d\kappa_{11} \\ = \frac{1}{2}D(\bar{\kappa}_{11})^2\]

\[\bar U_b = \frac{1}{2}M_{11}\bar{\kappa}_{11}\]

Caso General

La definición general de la densidad de energía de flexión dice:

\[\bar U_b = \oint M_{\alpha \beta} d\kappa_{\alpha \beta}\]

Figura\(\PageIndex{1}\): En una dimensión la densidad de energía es el área bajo la gráfica lineal momento-curvatura. En el caso multiaxial se puede alcanzar el valor final a lo largo de la trayectoria recta o no lineal.

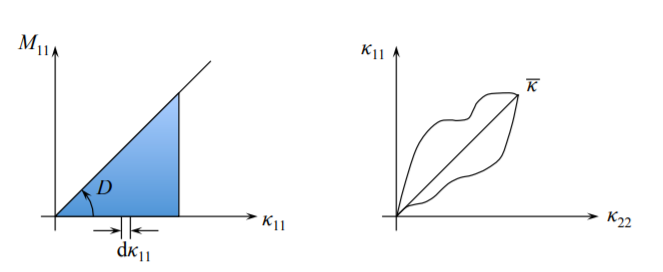
donde el símbolo\(\oint\) denota integración a lo largo de una determinada ruta de carga.

Calculemos la densidad de energía almacenada cuando la curvatura alcanza un valor dado\(\bar{\kappa}_{\alpha \beta}\) a lo largo de una trayectoria de carga recta:

\[\kappa_{\alpha \beta} = \eta \bar{\kappa}_{\alpha \beta}\]

\[d\kappa_{\alpha \beta} = \bar{\kappa}_{\alpha \beta}d\eta\]

Figura\(\PageIndex{2}\): La trayectoria de carga recta en el espacio tridimensional de los momentos de flexión.

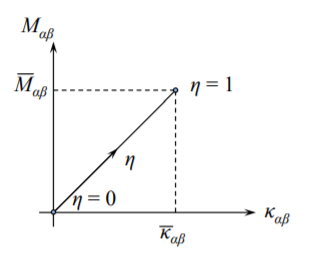
De la linealidad de la relación momento-curvatura, Ecuación\ ref {4.61}, se deduce que

\[M_{\alpha \beta} = \hat{M}_{\alpha \beta}(\kappa_{\alpha \beta}) \\ = \hat{M}_{\alpha \beta}(\eta\bar{\kappa}_{\alpha \beta}) \\ = \eta\hat{M}_{\alpha \beta}(\bar{\kappa}_{\alpha \beta})\]

donde\(\hat{M}_{\alpha \beta}(\kappa_{\alpha \beta})\) es una función homogénea de grado uno.

\[\bar U_b = \oint \hat{M}_{\alpha \beta}(\kappa_{\alpha \beta}) d\kappa_{\alpha \beta} \\ \int_{0}^{1} \eta \hat{M}_{\alpha \beta}(\bar{\kappa}_{\alpha \beta})\bar{\kappa}_{\alpha \beta}d\eta \\ = \hat{M}_{\alpha \beta}(\bar{\kappa}_{\alpha \beta})\bar{\kappa}_{\alpha \beta} \int_{0}^{1} \eta d\eta \\ \frac{1}{2} \hat{M}_{\alpha \beta}(\bar{\kappa}_{\alpha \beta})\bar{\kappa}_{\alpha \beta} \\ = \frac{1}{2} M_{\alpha \beta} \bar{\kappa}_{\alpha \beta}\]

Ahora, la densidad de energía de flexión dice

\[\bar U_b = \frac{D}{2} [(1 − \nu)\bar{\kappa}_{\alpha \beta} + \nu\bar{\kappa}_{\gamma \gamma}\delta_{\alpha \beta}] \bar{\kappa}_{\alpha \beta} \\ = \frac{D}{2} [(1 − \nu)\bar{\kappa}_{\alpha \beta}\bar{\kappa}_{\alpha \beta} + \nu\bar{\kappa}_{\gamma \gamma}\bar{\kappa}_{\alpha \beta}\delta_{\alpha \beta}] \\ = \frac{D}{2} [(1 − \nu)\bar{\kappa}_{\alpha \beta}\bar{\kappa}_{\alpha \beta} - \nu(\bar{\kappa}_{\gamma \gamma})^2]\]

La densidad de energía de flexión expresada en términos de componentes son:

\[\bar U_b = \frac{D}{2} \{(1 - \nu)[(\bar{\kappa}_{11})^2 + 2(\bar{\kappa}_{12})^2 + (\bar{\kappa}_{22})^2] + \nu(\bar{\kappa}_{11} + \bar{\kappa}_{22})^2\} \\ = \frac{D}{2} \{(1 - \nu) [(\bar{\kappa}_{11} + \bar{\kappa}_{22})^2 - 2\bar{\kappa}_{11}\bar{\kappa}_{22}+ 2(\bar{\kappa}_{12})^2 ] + \nu(\bar{\kappa}_{11} + \bar{\kappa}_{22})^2\} \\ = \frac{D}{2} \{(\bar{\kappa}_{11} + \bar{\kappa}_{22})^2 - 2\bar{\kappa}_{11}\bar{\kappa}_{22}+ 2(\bar{\kappa}_{12})^2 - \nu[-2\bar{\kappa}_{11}\bar{\kappa}_{22}+ 2(\bar{\kappa}_{12})^2]\} \\ = \frac{D}{2} \{(\bar{\kappa}_{11} + \bar{\kappa}_{22})^2 - 2\bar{\kappa}_{11}\bar{\kappa}_{22}+ 2(\bar{\kappa}_{12})^2 - \nu[-2\bar{\kappa}_{11}\bar{\kappa}_{22}+ 2(\bar{\kappa}_{12})^2]\} \\ = \frac{D}{2} \{(\bar{\kappa}_{11} + \bar{\kappa}_{22})^2 + 2(1-\nu) [-\bar{\kappa}_{11}\bar{\kappa}_{22}+ (\bar{\kappa}_{12})^2]\} \]

\[\boxed{\bar U_b = \frac{D}{2} \{(\bar{\kappa}_{11} + \bar{\kappa}_{22})^2 - 2(1 - \nu)[\bar{\kappa}_{11}\bar{\kappa}_{22} - (\bar{\kappa}_{12})^2]\}}\]

El término entre corchetes es la curvatura gaussiana,\(\kappa_G\), introducida en el Capítulo 1, Ecuación (1.8.9). Si la curvatura gaussiana se desvanece, como suele ser el caso en las placas, entonces la densidad de energía de flexión asume una forma muy simple\(\bar U_b = \frac{1}{2} D(\bar{\kappa}_{11} + \bar{\kappa}_{22})^2\).

Energía Total de Flexión

La energía total de flexión es la integral de la densidad de energía de flexión sobre el área de la placa:

\[U_b = \int_{S} \bar{U}_b dA\]

Fuerzas de membrana y energía de membrana

La fuerza axial se puede calcular de manera similar a la anterior

\[N_{\alpha \beta} = \frac{E}{1 − \nu^2} \int_{-\frac{h}{2}}^{\frac{h}{2}} [(1 − \nu)\epsilon_{\alpha \beta} + \nu\epsilon_{\gamma \gamma}\delta_{\alpha \beta}] dz \\ = \frac{E}{1 − \nu^2} \int_{-\frac{h}{2}}^{\frac{h}{2}} [(1 − \nu)\epsilon_{\alpha \beta}^{\circ} + \nu\epsilon_{\gamma \gamma}^{\circ}\delta_{\alpha \beta}] dz \\ + \frac{E}{1 − \nu^2} \int_{-\frac{h}{2}}^{\frac{h}{2}} [(1 − \nu)\kappa_{\alpha \beta} + \nu\kappa_{\gamma \gamma}\delta_{\alpha \beta}] z dz \\ = \frac{E}{1 − \nu^2} [(1 − \nu)\epsilon_{\alpha \beta}^{\circ} + \nu\epsilon_{\gamma \gamma}^{\circ}\delta_{\alpha \beta}] \int_{-\frac{h}{2}}^{\frac{h}{2}} dz \\ + \frac{E}{1 − \nu^2} [(1 − \nu)\kappa_{\alpha \beta} + \nu\kappa_{\gamma \gamma}\delta_{\alpha \beta}] \int_{-\frac{h}{2}}^{\frac{h}{2}} dz \\ = \frac{Eh}{1 − \nu^2} [(1 − \nu)\epsilon_{\alpha \beta}^{\circ} + \gamma\epsilon_{\gamma \gamma}^{\circ}\delta_{\alpha \beta}]\]

La integral\(\int_{-\frac{h}{2}}^{\frac{h}{2}} z dz\) es cero, lo que significa que no hay acoplamiento entre la fuerza de la membrana y las curvaturas.

Aquí definimos la rigidez axial de una placa de la\(C\) siguiente manera:

\[C = \frac{Eh}{1 − ν^2}\]

Ahora, se obtiene la relación fuerza-extensión de membrana en la notación tensora:

\[\boxed{N_{\alpha \beta} = C[(1 − \nu)\epsilon_{\alpha \beta}^{\circ} + \nu\epsilon_{\gamma \gamma}^{\circ}\delta_{\alpha \beta}]}\]

\[N_{\alpha \beta} = \begin{vmatrix} N_{11} & N_{12} \\ N_{21} & N_{22} \end{vmatrix}\]

donde\(N_{12} = N_{21}\) debido a la simetría. En componentes,

\[N_{11} = C(\epsilon_{11}^{\circ} + \nu\epsilon_{22}^{\circ})\]

\[N_{22} = C(\epsilon_{22}^{\circ} + \nu\epsilon_{11}^{\circ})\]

\[N_{12} = C(1 - \nu) \epsilon_{11}^{\circ}\]

Densidad de energía de membrana

Usando la definición similar utilizada en el cálculo de la densidad de energía de flexión, la energía de extensión (energía de membrana) dice:

\[\bar {U}_m = \oint N_{\alpha \beta} d\epsilon_{\alpha \beta}^{\circ}\]

Calculemos la energía almacenada cuando la extensión alcance un valor dado\(\bar{\epsilon}_{\alpha \beta}^{\circ}\). Considera un camino recto:

\[\epsilon_{\alpha \beta}^{\circ} = \eta\bar{\epsilon}_{\alpha \beta}^{\circ}\]

\[d\epsilon_{\alpha \beta}^{\circ} = \bar{\epsilon}_{\alpha \beta}^{\circ} d\eta\]

\[N_{\alpha \beta} = \hat{N}_{\alpha \beta}(\epsilon_{\alpha \beta}^{\circ}) \\ = \hat{N}_{\alpha \beta}(\eta\bar{\epsilon}_{\alpha \beta}^{\circ}) \\ = \eta\hat{N}_{\alpha \beta}(\bar{\epsilon}_{\alpha \beta}^{\circ})\]

donde\(\hat{N}_{\alpha \beta}(\epsilon_{\alpha \beta}^{\circ})\) es una función homogénea de grado uno.

\ [\ bar {U} _m =\ int_ {0} ^ {\ bar {\ épsilon} _ {\ alfa\ beta} ^ {\ circ}}\ hat {N} _ {\ alpha\ beta} (\ épsilon_ {\ alpha\ beta} ^ {\ circ}) d\ épsilon_ {\ alpha\ beta} ^ {\ circ}\\ = int_ _ {0} ^ {1}\ eta\ sombrero {N} _ {\ alfa\ beta} (\ bar {\ épsilon} _ {\ alfa\ beta} ^ {\ circ})\ bar {\ épsilon} _ {\ alfa\ beta} ^ {\ circ} d\ eta\\
=\ frac {1 } {2}\ hat {N} _ {\ alpha\ beta} (\ bar {\ épsilon} _ {\ alpha\ beta} ^ {\ circ})\ bar {\ épsilon} _ {\ alpha\ beta} ^ {\ circ}\\
=\ frac {1} {2} N_ {\ alpha\ beta}\ bar {\ épsilon} _ {\ alpha\ beta\} ^ {\ circ}\]

Ahora, la energía de extensión dice:

\[\tilde{U}_m = \frac{C}{2} [(1-\nu) \bar{\epsilon}_{\alpha \beta}^{\circ} + \nu \bar{\epsilon}_{\gamma \gamma}^{\circ} \delta_{\alpha \beta} ] \bar{\epsilon}_{\alpha \beta}^{\circ} \\ = \frac{C}{2} [ (1-\nu) \bar{\epsilon}_{\alpha \beta}^{\circ} \bar{\epsilon}_{\alpha \beta}^{\circ} + \nu ( \bar{\epsilon}_{\gamma \gamma}^{\circ} )^{2} ] \]

La densidad de energía de extensión expresada en términos de componentes es:

\ [\ bar {U} _m =\ frac {C} {2}\ {(1-\ nu) [(\ bar {\ épsilon} _ {11} ^ {\ circ}) ^ {2} + 2 (\ bar {\ épsilon} _ {12} ^ {\ circ}) ^ {2} + (\ bar {\ épsilon} _ {22} ^ {^\ circ}) ^ {2}] +\ nu (\ bar {\ épsilon} _ {11} ^ {\ circ} +\ bar {\ épsilon} _ {22} ^ {\ circ}) ^ {2}\}\}\
=\ frac {C} {2}\ {(1-\ nu) [(\ bar {\ épsilon} _ {11} ^ {\ circ} +\ bar {\ épsilon} _ { 22} ^ {\ circ}) ^ {2} - 2\ bar {\ épsilon} _ {11} ^ {\ circ}\ bar {\ épsilon} _ {22} ^ {\ circ} +2 (\ bar {\ épsilon} _ {12} ^ {\ circ}) ^ {2}] +\ nu (\ bar {\ épsilon} _ {11} ^ {\ circ} +\ bar {\ épsilon} _ {22} ^ {\ circ}) ^ {2}\}\}\
=\ frac {C} {2}\ {(\ bar {\ épsilon} _ {11} ^ {\ circ} +\ bar {\ épsilon} _ {22} ^ {\ circ}) ^ {2} - 2\ bar\ épsilon} _ {11} ^ {\ circ}\ bar {\ épsilon} _ {22} ^ {\ circ} + 2 (\ bar {\ épsilon} _ {12} ^ {\ circ}) ^ {2} -\ nu [-2\ bar {\ épsilon} _ {11} ^ {\ circ}\ bar {\ épsilon} _ {22} ^ {\ circ} + 2 (\ bar {\ épsilon} _ {12} ^ {\ circ}) ^ {2}]\}\}\
=\ frac {C} {2}\ {(\ bar {\ épsilon} _ {11} ^ {\ circ} +\ bar {\ épsilon} _ {22} ^ {\ circ}) ^ {2} + 2 (1-\ nu) [-\ barra {\ épsilon} _ { 11} ^ {\ circ}\ bar {\ épsilon} _ {22} ^ {\ circ} + (\ bar {\ épsilon} _ {12} ^ {\ circ}) ^ {2}]\}\]

\[\boxed{\bar{U}_m = \frac{C}{2} \{ (\bar{\epsilon}_{11}^{\circ} + \bar{\epsilon}_{22}^{\circ} )^{2} - 2(1-\nu) [\bar{\epsilon}_{11}^{\circ} \bar{\epsilon}_{22}^{\circ} - (\bar{\epsilon}_{12}^{\circ} )^{2} ] \} }\]

La energía total de la membrana es la integral de la densidad de energía de la membrana sobre el área de la placa:

\[U_m = \int_{S} \bar{U}_m dS\]