4.3: Vigas Estáticamente Determinadas
- Page ID
- 85150
Las vigas para las que la distribución de los momentos de flexión y las fuerzas de cizallamiento se pueden determinar a partir del equilibrio solo se denominan vigas estáticamente determinadas. Para tales vigas\(M(x)\) y\(V (x)\) son conocidas y la determinación de la desviación del haz será una tarea mucho más fácil. Combinando la Ecuación (4.1.9) con la Ecuación (4.1.2) uno termina con la siguiente ecuación diferencial lineal de segundo orden
\[−EI \frac{d^2w}{dx^2} = M(x) \label{4.3.1}\]
El momento de flexión, que por sí mismo debería satisfacer la ecuación diferencial de segundo orden, la Ecuación (4.1.7) debería obedecer ahora dos condiciones de límite de tensión en los extremos de la viga. Las condiciones de límite estático se indican en la Figura (\(\PageIndex{1}\)) para una viga soportada por pasador y en voladizo.
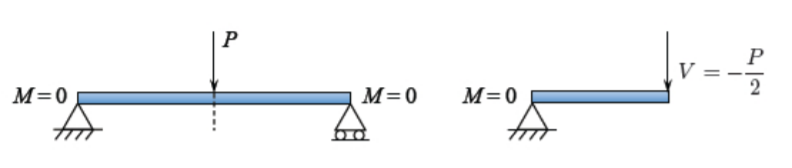
La determinación de los diagramas de momento de flexión y fuerza de corte es objeto de cursos elementales en estática, y aquí no se explica el procedimiento general. En el caso de la viga simplemente soportada con una carga puntual en el tramo medio, los momentos de flexión
\[M(x) = \begin{cases} \frac{P x}{2} , & 0 < x < \frac{l}{2} \\ \frac{P(l − x)}{2} , & \frac{l}{2} < x < l \end{cases} \label{4.3.2}\]
El momento de flexión se desvanece a las\(x = 0\) y\(x = l\).
La fuerza cortante correspondiente\(V = \frac{dM}{dx}\) es
\[V(x) = \begin{cases} \frac{P}{2} , & 0 < x < \frac{l}{2} \\ - \frac{P}{2} , & \frac{l}{2} < x < l \end{cases} \]
En el centro de la viga
\[[V ] = \frac{P}{2} − \left[ − \frac{P}{2} \right] = P\]
Debido a la discontinuidad de la fuerza de corte en el centro de la viga, se buscará la solución para la mitad de la viga. Cada mitad de la viga lleva la mitad de la carga. Hemos demostrado que la distribución del momento de flexión satisface dos condiciones de límite satinado. Por lo tanto, la ecuación diferencial\ ref {4.3.2} se somete solo a dos condiciones de límite cinemáticas
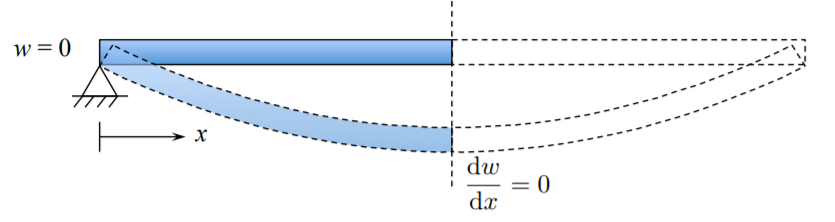
Integrando Ecuación\ ref {4.3.1} dos veces uno obtiene
\[−EIw = \frac{P x^3}{12} + C_1x + C_2\]
Las dos constantes de integración, determinadas a partir de las condiciones límite\(w(0) = 0, \quad \left. \frac{dw}{dx} \right|_{ x= \frac{l}{h}} = 0\), son
\[C_1 = −\frac{Pl^2}{16}, \quad C_2 = 0\]
y la línea de deflexión de la viga viene dada por
\[w(x) = \frac{Px}{48EI} (3l^2 - 4x^2) \quad 0 < x < \frac{l}{2}\]
La segunda mitad del haz es el reflejo del espejo, por simetría. En particular, la deflexión central\(w_o = w(x = \frac{l}{2})\) se expresa por todos los parámetros de entrada del haz como
\[w_o = \frac{Pl^3}{48EI}\]
Te será útil recordar la fórmula anterior para el resto de tu vida profesional.
En resumen, la determinación de las deflexiones de haces estáticamente determinados es mucho más fácil que sus contrapartes estáticamente indeterminadas. La ecuación gobernante es de segundo orden, y para problemas simétricos solo hay dos constantes de integración.