5.3: Solución para una Viga con Desplazamientos Axiales Fijos
- Page ID
- 85100
El problema se resuelve bajo el supuesto de una condición final simplemente soportada, y la carga de línea se distribuye de acuerdo con la función coseno. La viga está restringida en la dirección axial. Existe un considerable efecto de fortalecimiento de la respuesta del haz debido a las rotaciones finitas de los elementos del haz. La fuerza axial\(N\) (distinta de cero esta vez) se calcula a partir de la Ecuación (5.1.6-5.1.7) con la Ecuación (5.1.1)
\[N = EA \left[\frac{du}{dx} + \frac{1}{2}\left(\frac{dw}{dx}\right)^2\right] \label{6.15} \]
De la Ecuación (5.1.4) sabemos que\(N\) es constante pero desconocido. Para hacer uso de las condiciones de contorno cinemático, integremos ambos lados de la Ecuación\ ref {6.15} con respecto a\(x\)
\[\frac{Nl}{EA} = u(l) - u(0) + \int_{0}^{l} \frac{1}{2} \left( \frac{dw}{dx}\right)^2 dx\]
Usando las condiciones de límite para\(u\), la fuerza axial se relaciona con el cuadrado de la pendiente por
\[\frac{Nl}{EA} = \frac{1}{2} \int_{0}^{l} \left( \frac{dw}{dx}\right)^2 dx \label{6.17}\]
Para determinar la forma desviada de la viga, considere el equilibrio en la dirección vertical dado por la Ecuación (5.1.5)
\[−EI \frac{d^4w}{dx^4} + N \frac{d^2w}{dx^2} + q = 0 \label{6.18}\]
Dividiendo ambos lados por\((−EI)\) uno obtiene
\[\frac{d^4w}{dx^4} − \lambda^2 \frac{d^2w}{dx^2} = \frac{q_o}{EI} \cos \frac{\pi x}{l}\]
donde
\[\lambda^2 = \frac{N}{EI}\]
Las raíces de las ecuaciones características son\(0, 0, \pm \lambda\). Por lo tanto, la solución general de la ecuación homogénea es
\[w_g = C_o + C_1x + C_2 \cosh \lambda x + C_3 \sinh \lambda x\]
Como solución particular de la ecuación no homogénea podemos intentar
\[w_p(x) = C \cos \frac{\pi x}{l}\]
\[\frac{d^2w_p}{dx^2} = − \frac{\pi^2}{l^2} C \cos \frac{\pi x}{l}\]
\[\frac{d^4w_p}{dx^4} = \frac{\pi^4}{l^4} C \cos \frac{\pi x}{l}\]
Sustituyendo la solución anterior por la ecuación gobernante\ ref {6.18} se obtiene
\[\left[ \frac{\pi^4}{l^4} C - \lambda^2 \frac{\pi^2}{l^2} C - \frac{P_o}{EI} \right] \cos \frac{\pi x}{l} = 0\]
La solución anterior satisface la ecuación diferencial si la amplitud\(C\) está relacionada con los parámetros de entrada y la tensión desconocida\(N\)
\[C = \frac{\frac{q_o}{EI}}{\frac{\pi^2}{l^2} \left(\lambda^2 + \frac{\pi^2}{l^2} \right)} = \frac{q_o}{EI \left(\frac{\pi}{l}\right)^4 + N\left(\frac{\pi}{l}\right)^2} \label{6.24}\]
La solución general de la Ecuación\ ref {6.18} es una suma de la solución particular de la ecuación no homogénea\(w_p\) y la solución general de la ecuación homogénea,\(w_g\)
\[w(x) = w_g + w_p \]
Hay cinco incógnitas,\(C_o, C_1, C_2, C_3\)\(N\) y cinco ecuaciones. Cuatro condiciones límite para las deflexiones transversales
\[w = 0, \quad \frac{d^2w}{dx^2} = 0 \quad \text{ at } \quad x = \pm \frac{l}{2}\]
y ecuación\ ref {6.17} relacionando la respuesta horizontal y vertical. La determinación de las constantes de integración es sencilla. Tenga en cuenta que el problema es simétrico. Por lo tanto la solución debe ser una función par 1 de\(x\). Los términos\(C_1x\) y\ (C_3\ sinh\ lambda x son funciones impares. Por lo tanto, los coeficientes respectivos deben desaparecer
\[C_1 = C_3 = 0 \]
\[w(x) = C_o + C_2 \cosh \lambda x + C \cos \frac{\pi x}{l} \label{6.28}\]
Los dos coeficientes restantes se determinan solo a partir de las condiciones de contorno en un lado de la viga
\[\begin{array} w(x = \frac{l}{2} ) = 0 \rightarrow \\ \left. \frac{d^2w}{dx^2}\right|_{x = \frac{l}{2}} = 0 \rightarrow \end{array} \begin{cases} C_o + C_2 \cosh \frac{\lambda l}{2} = 0 \\ C_2\lambda^2 \cosh \frac{\lambda l}{2} = 0 \end{cases}\]
La solución del sistema anterior es
\[C_o = C_2 = 0\]
La pendiente de la curva de deflexión, calculada a partir de la Ecuación\ ref {6.28} es
\[\frac{dw}{dx} = −C \frac{\pi}{2} \sin \frac{\pi x}{2} \]
Expresando\(N\) en términos de\(x\) en la Ecuación\ ref {6.17} da
\[\lambda^2 \left(\frac{Il}{A}\right) = \frac{1}{2} \int_{0}^{l} \left( \frac{dw}{dx}\right)^2 dx\]
Combinando las dos ecuaciones anteriores, uno obtiene
\[\lambda^2 \left(\frac{Il}{A}\right) = \frac{1}{2} \int_{0}^{l} \left( - \frac{C\pi}{l} \sin \frac{\pi x}{l} \right)^2 dx\]
o después de la integración
\[\frac{\lambda^2 Il}{A} = \frac{1}{4} C^2 \left(\frac{\pi}{l} \right)^2 \frac{l}{2}\]
Recordando la definición de\(\lambda\), la fuerza de membrana\(N\) se convierte en una función cuadrática de la amplitud de deflexión
\[N = \frac{EA}{4}C^2 \left(\frac{\pi}{l}\right)^2 \label{6.35}\]
La fuerza de membrana se puede eliminar entre las ecuaciones\ ref {6.24} y\ ref {6.35} para dar la ecuación cúbica para la amplitud de deflexión\(C\)
\[C + C^3 \frac{A}{4I} = \frac{q_o}{EI} \left(\frac{l}{\pi}\right)^4 \label{6.36}\]
Para tener una mejor idea de la contribución de diversos términos, considere una viga de sección transversal cuadrada\(h \times h\), para lo cual
\[I = \frac{h}{12}, \; A = h^2, \; \frac{A}{I} = \frac{12}{h^2}\]
Además, la deflexión ventral se dimensiona con respecto al grosor del haz\(\bar{w}_o = \frac{C}{h}\)
\[\bar{w}_o + 3w^{3}_o = \left(\frac{q_o}{Eh}\right) \left( \frac{l}{\pi h} \right)^4 \label{6.38}\]
La presente solución es exacta e involucra toda la información sobre el material\((E)\), la intensidad\((q_o)\) de carga, la longitud\((l)\) y la dimensión de la sección transversal. La distribución de la carga de línea y las condiciones de límite se reflejan en los coeficientes numéricos específicos en los términos respectivos.
Para obtener una visión física sobre las contribuciones de todos los términos en la solución anterior, considere dos casos limitantes:
- Solución de flexión pura para la cual\(N \frac{dw}{dx} = 0\).
- Solución de membrana pura (cuerda, cable) con cero resistencia a la flexión (rigidez a la flexión\(EI \rightarrow 0\)).
(i) La solución de flexión se obtiene dejando caer el término cúbico en Ecuaciones\ ref {6.36} o\ ref {6.38}
\[C = \frac{q_ol^4}{EI} \frac{1}{\pi^4} \label{6.39}\]
donde el coeficiente\(\pi^4 = 97.4\). este resultado para la distribución sinusoidal de la carga lineal debe compararse con la carga lineal uniforme (coeficiente 77) y la carga puntual (coeficiente 48).
(ii) La solución de membrana se recupera al descuidar el primer término lineal
\[C^3 = \frac{q_ol^4}{EI} \frac{4}{\pi^4} \label{6.40}\]
La gráfica de la solución de doblado/membrana completa y dos casos limitantes se muestra en la Figura (\(\PageIndex{1}\)).
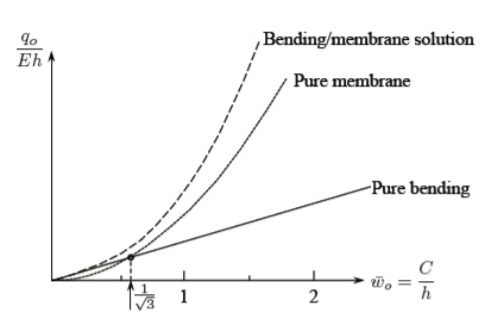
La pregunta es en qué magnitud de la deflexión central en relación con el espesor de la viga la carga no dimensional\(\frac{q_o}{Eh}\) es la misma. Esta es la intersección de la línea recta con la parábola de tercer orden. Al eliminar el parámetro de carga entre las ecuaciones\ ref {6.39} y\ ref {6.40} se obtiene
\[C^2 = \frac{4I}{A} = \frac{4\rho^2 A}{A} = 4\rho^2\]
donde\(\rho\) está el radio de giro de la sección transversal. Para una sección transversal cuadrada
\[C = 2\rho = 2\sqrt{\frac{I}{\rho}} = 2\sqrt{\frac{h^4}{12h^2}} = \frac{h}{\sqrt{3}} \cong 0.58h\]
Se concluye que la transición de la flexión a la acción de la membrana ocurre bastante temprano en la respuesta del haz. Como regla general, la solución de flexión en la viga restringida por el movimiento axial se restringe a deflexiones iguales a la mitad del grosor de la viga. Si las deflexiones son mayores, la respuesta de la membrana domina. Por ejemplo, si la deflexión del haz alcanza tres espesores, la contribución de flexión y acción de membrana es 3:81. En el límite superior de la aplicabilidad de la teoría de la desviación moderadamente grande de las vigas\(C \cong 10h\), la contribución de la resistencia a la flexión es solo 0.3% de la resistencia de la membrana.
La rápida transición de la flexión a la acción de membrana solo está presente para vigas restringidas axialmente. Si la viga es libre de deslizarse en la dirección axial, no se desarrolla resistencia de membrana y la carga siempre está relacionada linealmente con las deflexiones.
La solución de forma cerrada elegante anterior se obtuvo para la distribución sinusoidal particular de la carga lineal, la cual coincide con la forma desviada de la viga. Para una carga arbitraria, solo se pudieron derivar soluciones aproximadas. Uno de tales métodos de solución, aplicable a la amplia clase de problemas no lineales para placas y conchas se llama el método Galerkin.
1 La función es incluso cuando\(f(−A) = f(A)\). La función es impar cuando\(f(−A) = −f(A)\).


