6.5: Placas Sandwich
- Page ID
- 85232
Las placas sándwich están compuestas por láminas de cara y un núcleo ligero, Figura (\(\PageIndex{1}\)).
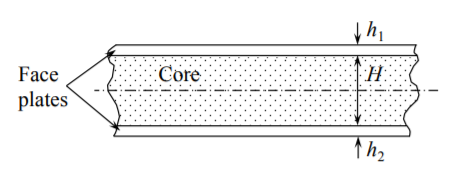
El núcleo está transmitiendo esfuerzos cortantes mientras que las placas de cara están trabajando principalmente en tensión o compresión. Los materiales típicos para un núcleo son espuma de poliuritina, espuma de aluminio, panales de aluminio o nomex, material polimérico de diversos tipos etc. En muchas estructuras de acero, hay un núcleo discreto hecho de láminas corrugadas soldadas rigidizadores de diferentes topologías o estructuras de celosía. En la Figura (6.6.1) se muestran imágenes de algunos materiales de núcleo típicos y conjuntos sándwich.
Para determinar la flexión y rigidez axial de la placa sándwich, debemos revisar la definición de momento de flexión. Para doblado cilíndrico,
\[M_{xx} = \int \sigma z dz = \int_{-\frac{H}{2}}^{\frac{H}{2}} \sigma_cz dz + \sigma_f hH \label{7.48a}\]
\[N_{xx} = \int \sigma dz = \int_{-\frac{H}{2}}^{\frac{H}{2}} \sigma_c dz + 2\sigma_f h \label{7.48b}\]
El módulo de Young del material del núcleo suele ser dos órdenes de magnitud menor que el de las placas de cara, entonces\(\sigma_f \gg \sigma_c\). Despreciando el primer término en la Ecuación\ ref {7.48a} -\ ref {7.48b} y extendiendo las definiciones anteriores a las placas, los momentos de flexión y las fuerzas axiales son
\[M_{\alpha \beta} = \sigma_{\alpha \beta}hH \]
\[N_{\alpha \beta} = 2\sigma_{\alpha \beta}h \]
donde\(\sigma_{\alpha \beta}\) se relaciona con la deformación de la placa frontal por la ley de elasticidad de tensión plana, Ecuaciones (3.6.1- 3.6.5). La hipótesis de Love-Kirchhoff sigue siendo válida por lo que las cepas en las placas faciales son
\[\epsilon_{\alpha \beta} = \epsilon_{\alpha \beta}^{\circ} \pm \frac{H}{2} \kappa_{\alpha \beta}\]
donde el letrero “\(\pm\)” se aplica al lado de tracción y compresión del panel. Las relaciones momento-curvatura resultantes se convierten en
\[M_{\alpha \beta} = D_s[(1 − \nu)\kappa_{\alpha \beta} + \nu\kappa_{\gamma \gamma}\delta_{\alpha \beta}] \]
\[N_{\alpha \beta} = C_s[(1 − \nu) \epsilon_{\alpha \beta}^{\circ} + ν\epsilon_{\gamma\gamma} \delta_{\alpha \beta}] \]
donde se encuentran las rigideces axiales y de flexión de las placas sándwich
\[D_s = \frac{EhH^2}{(1 − \nu^2)}; \quad C_s = \frac{EhH}{1 − \nu^2} \label{7.52}\]
Ahora, hay más espacio para el diseño óptimo, ya que en lugar de un grosor de una placa monolítica, tenemos dos parámetros geométricos con los que jugar. Sustituyendo la rigidez a la flexión\(D\) de la placa monolítica por la ecuación\ ref {7.52}, la rigidez a la flexión de la placa sándwich circular se vuelve
\[K_s = 222E \frac{hH^2}{R^2} \]
Suponiendo que la densidad de masa del núcleo sea dos órdenes de magnitud menor que la placa frontal, el peso total de la placa sándwich es
\[W_s = \pi R^2 2h\rho \]
Entonces, la fórmula para la rigidez a la flexión por unidad de peso es
\[\bar{K}_s = 35 \frac{E}{\rho}\frac{H^2}{R^4} \left[\frac{N}{mKg}\right] \]
Se pueden hacer dos observaciones. Primero,\(K_s\) es independiente del grosor de las placas de cara. En segundo lugar, la rigidez por unidad de peso aumenta parabólicamente con el grosor del núcleo\(H\). ¿Significa que uno puede hacer\(K_s\) tan grande como se desee aumentando\(H\)? Esto es demasiado bueno para ser verdad. Al aumentar\(H\), la placa sándwich puede fallar en cualquiera de los tres modos de falla:
- El rendimiento o fractura de la placa frontal en el lado de tracción;
- Pandeo de la placa frontal en el lado compresivo;
- Delaminación por cizallamiento excesivo.
Ninguno de estos modos de falla está presente en placas monolíticas. Se puede concluir que las placas sándwich aportan mejoras sustanciales en la rigidez a la flexión pero al mismo tiempo introducen nuevas características no deseadas. Fractura, pandeo y esfuerzos cortantes serán objeto de conferencia posterior. Pero incluso en este punto podemos decir que la optimización de las placas sándwich son posibles al determinar el grosor máximo del núcleo\(H_{opt}\) ligeramente menor que el que provoca uno de los modos de falla anteriores.


