7.4: Expansión de la Serie de Fourier y el Método Ritz
- Page ID
- 85094
Considere una placa cargada simétricamente simplemente soportada por la fuerza puntual en el centro. La energía potencial total del sistema es
\[\prod = \int_{0}^{l} \frac{EI}{2} (w^{\prime\prime})^2 dx − P w \]
El objetivo es encontrar la amplitud y forma de la función de deflexión que esté en equilibrio con la carga prescrita\(P\). En otras palabras, estaremos buscando la deflexión y forma que hará que la energía potencial total sea estacionaria.
Asumir la solución como una función de expansión de Fourier
\[w(x) = \sum^{N}_{n=1} a_n \phi_n(x) \label{8.24}\]
donde\(\phi_n(x)\) es un sistema completo de función de coordenadas que satisface las condiciones de contorno cinemático. En el sistema de coordenadas rectangulares este sistema consiste en funciones hormonicas, en el sistema de coordenadas polares estas son la función de Bessel, y en el sistema de coordenadas esféricas este papel es asumido por las funciones Legender. En nuestro caso
\[\phi_n(x) = \sin \frac{ n \pi x}{l} \label{8.25}\]
Las condiciones de contorno cinemáticas\(\phi_n(x = 0) = \phi_n(x = l)\) se satisfacen de manera idéntica. Además, debido a la simetría del problema, solo la función simétrica contribuirá a la solución.
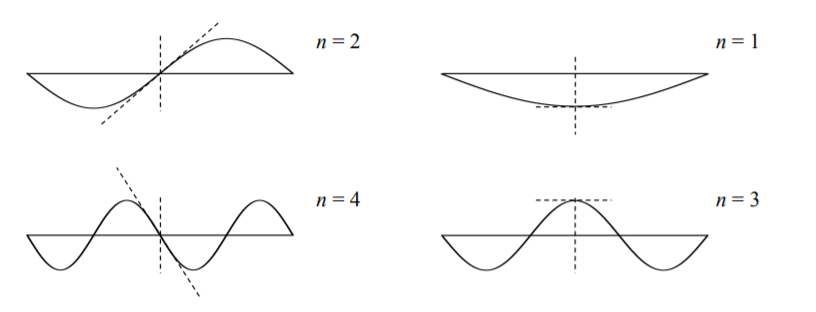
La solución se representa entonces como
\[w(x) = a_1 \sin \frac{\pi x}{l} + a_3 \sin \frac{3 \pi x}{l} + \dots \label{8.26}\]
Considerar la primera aproximación a un término
\[w(x) = a_1 \sin \frac{\pi x}{l} \]
\[w^{\prime}(x) = a_1 \left( \frac{\pi}{l} \right) \cos \frac{\pi x}{l} \]
\[w^{\prime\prime}(x) = −a_1 \left( \frac{\pi}{l} \right)^2 \sin \frac{\pi x}{l} \]
La expresión de la energía potencial total es
\[\prod = \frac{1}{2} EI \left( \frac{\pi}{l} \right)^4 a^2_1 \int_{0}^{l} \sin \frac{\pi x}{l}- P a_1 \]
donde la integral es simplemente\(l/2\). La ecuación\ ref {8.26} reduce entonces a
\[\prod = \frac{1}{4} EI \frac{\pi^4}{l^3} a^2_1 − P a_1 \]
Para el equilibrio\(\frac{d\prod}{da_1} = 0\), que rinde
\[\frac{1}{2} EI \frac{\pi^4}{l^3} a_1 − P = 0\]
La relación carga-desplazamiento viene dada finalmente por
\[(a_1)_{\text{opt}} = \frac{Pl^3}{\frac{\pi^4}{2}EI} = \frac{Pl^3}{48.7EI} \]
El coeficiente numérico en la solución exacta de este problema es 48. El error de la solución aproximada es de 1.4%. Una precisión tan buena de solo una aproximación a un término se puede explicar haciendo la expansión de la serie Taylor de la función de signo
\[\sin \frac{\pi x}{l} = \frac{\pi x}{l} − \frac{1}{6} \left( \frac{\pi x}{l} \right)^3 + \dots \]
La expansión de dos términos tiene un término lineal y cúbico en\(x\), lo mismo que la solución exacta.
Examinemos a continuación la propiedad estacionaria de lo funcional\(\prod\). Definir la energía potencial total normalizada como\(\bar{\prod} = \frac{\prod}{P w_o}\), uno obtiene
\[\bar{\prod} = \frac{1}{2} \frac{a_1}{w_o} \left(\frac{a_1}{w_o} − 2 \right) \]
donde\(a_1\) está la amplitud de la función de ensayo Ecuación\ ref {8.25} y\(w_o\) es la amplitud exacta. La gráfica de la función\(\bar{\prod} (a_1)\) se muestra en la Figura (\(\PageIndex{2}\)).
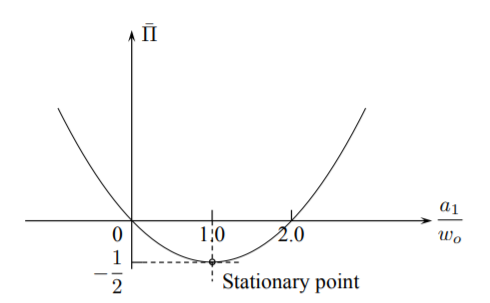
La función\(\bar{\prod}(a_1)\) es una parábola con un punto estacionario en\(a_1 = w_o\). El punto estacionario es al mismo tiempo el mínimo. El valor negativo del valor mínimo (real) de la energía potencial total proviene de la elección del nivel de referencia de la energía potencial. En mecánica, el nivel de referencia es la posición del eje no deformado de la viga. Al cargar, el haz pierde la energía potencial y el segundo término en la Ecuación (7.3.3) es negativo y mayor que el primer término de la energía elástica almacenada.
A pesar de que la precisión de la aproximación de un término en la expansión de la serie de Fourier, la Ecuación (7.3.4) dio una muy buena aproximación (1.4% de error), la solución se puede mejorar aún más considerando el siguiente término en la expansión, de acuerdo con la Ecuación\ ref {8.24}. En este caso la energía potencial total es la función de dos amplitudes desconocidas,\(\prod = \prod(a_1, a_3)\) y la solución se obtiene a partir de dos ecuaciones algebraicas
\[\frac{\partial \prod}{\partial a_1} = 0, \quad \frac{\partial \prod}{\partial a_3} = 0 \]


