8.3: Estabilidad de la Columna Elástica Usando el Método Energético
- Page ID
- 85129
La condición Trefftz para la estabilidad ahora se puede extender a la columna elástica sometida a flexión y compresión combinadas. La energía de deformación elástica almacenada en la columna es una suma de la contribución de flexión y fuerza axial
\[U = \int_{0}^{l} \left( \frac{1}{2} M \kappa + \frac{1}{2} N \epsilon_o \right) dx \]
Se supone que la columna se fija en un extremo contra el movimiento axial y permite moverse en la dirección de la fuerza axial.
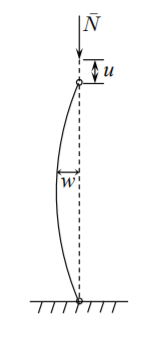
Para mantener la generalidad, no se introducen condiciones de límite estáticas o cinemáticas en la presente derivación. El trabajo de las fuerzas externas es
\[W = \bar{N}u_o \]
La primera variación de la energía potencial total es
\[\delta\prod = \delta (U − W) = \frac{1}{2} \int_{0}^{l} (\delta M\kappa + M\delta\kappa + \delta N \epsilon + N\delta \epsilon)dx − N\delta u_o \label{8.3.3}\]
Para material elástico lineal
\[M = EI \kappa, \quad \delta M = EI \delta \kappa \]
\[N = EA \epsilon, \quad \delta N = EA \delta \epsilon \]
Al eliminar la flexión y la rigidez axial entre la ecuación anterior, se mantienen las siguientes identidades
\[M \delta \kappa = \delta M \kappa \]
\[N \delta \epsilon = \delta N \epsilon\]
Por lo tanto, la expresión\ ref {8.3.3} se reduce a
\[\delta\prod = \int_{0}^{l} (M\delta \kappa + N\delta \epsilon) dx − \bar{N}\delta u_o \label{8.3.8}\]
Ahora, recordemos las relaciones deformación-desplazamiento en la teoría de la desviación moderadamente grande de las vigas
\[\kappa = −w^{\prime \prime}, \quad \delta \kappa = −(\delta w)^{\prime \prime} \]
\[\epsilon = u^{\prime} + \frac{1}{2} (w^{\prime})^2 , \quad \delta\epsilon = (\delta u)^{\prime} − w^{\prime} \delta w^{\prime} \]
Sustituyendo los incrementos\(\delta\kappa\) y\(\delta\epsilon\) en Ecuación\ ref {8.3.8} rendimientos
\[\delta \prod = − \int_{0}^{l} M \delta w^{\prime \prime} dx + N \int_{0}^{l} w^{\prime} \delta w^{\prime} dx + N \int_{0}^{l} \delta u^{\prime} dx − N\delta u_o \label{8.3.11}\]
En la expresión anterior la carga axial es desconocida pero constante a lo largo de la columna. Por lo tanto, la carga\(N\) podría llevarse fuera de las integrales. Consideremos ahora los dos últimos términos en la Ecuación\ ref {8.3.11}
\[N \int_{0}^{l} \delta u^{\prime} dx − N\delta u_o = \left. N\delta u\right|^{x=l}_{x=0} − N\delta u = N\delta u_o − N\delta u_o = 0 \]
Con la simplificación anterior calculamos ahora la segunda variación de la energía potencial total
\[\delta^2 \prod = \delta (\delta\prod) = − \int_{0}^{l} \delta M\delta w^{\prime \prime} dx + N \int_{0}^{l} \delta w^{\prime} \delta w^{\prime} dx \]
Según el criterio de estabilidad de Trefftz\(\delta^2\prod = 0\),
\[− \int_{0}^{l} EI \delta w^{\prime\prime} \delta w^{\prime\prime} dx + N \int_{0}^{l} \delta w^{\prime} \delta w^{\prime} dx = 0 \]
La carga de pandeo\(N = N_c\) es entonces
\[N = EI \frac{− \int_{0}^{l}\delta w^{\prime\prime} \delta w^{\prime\prime} dx}{\int_{0}^{l} \delta w^{\prime} \delta w^{\prime} dx} \label{8.3.15}\]
Expresemos la desviación fuera del plano de la columna como producto de la amplitud\(A\) y la función de forma normalizada\(\phi(x)\). La función shape debe satisfacer la condición de límite cinemático de un problema
\[w(x) = A \phi (x) \]
Podemos calcular ahora la primera y segunda derivadas de la función\(w(x)\) y sus variaciones
\[w^{\prime} = A\phi^{\prime}, \quad \delta w^{\prime} = \delta A\phi^{\prime} \]
\[w^{\prime\prime} = A\phi^{\prime\prime}, \quad \delta w^{\prime\prime} = \delta A\phi^{\prime\prime}\]
Sustituyendo la expresión anterior en Ecuación\ ref {8.3.15}, obtenemos
\[N_c = EI \frac{\int_{0}^{l} \delta A\phi^{\prime\prime} \delta A\phi^{\prime\prime} dx }{\int_{0}^{l} \delta A\phi^{\prime} \delta A\phi^{\prime} dx} = EI \frac{\int_{0}^{l} \phi^{\prime\prime} \phi^{\prime\prime} dx}{\int_{0}^{l} \phi^{\prime} \phi^{\prime} dx} \]
donde\(N_c = -N\) esta la carga de pandeo compresivo.
La ecuación anterior para la carga crítica de pandeo de una columna se denomina cociente de Raleigh-Ritz. El criterio Trefftz no proporciona la función shape pero para una forma determinada calcula el valor aproximado de la carga de pandeo. Este es siempre un límite superior. Si la función shape coincide con la forma exacta de pandeo, el cociente Raleigh-Ritz dará el valor mínimo absoluto.
Como ilustración, considere la columna soportada por pin y asuma la siguiente forma de pandeo
\[\phi (x) = x(l − x) \label{8.3.20}\]
que satisface condiciones de contorno cinemáticas idénticas\(\phi (x = 0) = \phi (x = l) = 0\). La primera y segunda derivadas de la función shape son
\[\phi^{\prime} (x) = 2x − l \]
\[\phi^{\prime\prime} (x) = 2 \]
Después de una integración sencilla, la carga de pandeo calculada es
\[N_c = \frac{12EI}{l^2} \]
¿Se puede mejorar la precisión de la solución anterior? Intentemos asumir como función de forma la solución para la viga pin pin bajo la carga de línea uniforme
\[\phi (x) = x^4 − 2lx^3 + l^3x \]
La función anterior satisface la condición de límite de soporte simple en ambos extremos. La pendiente y la curvatura de la forma desviada son
\[\phi^{\prime}(x) = 4x^3 − 6lx^2 + l^3 \]
\[\phi^{\prime\prime}(x) = 12x^2 − 12lx \]
Debido a que la curvatura en ambos extremos se desvanece, también lo hace el momento de flexión. También la pendiente a mitad de tramo es cero. Esto significa que también se satisfacen las condiciones de límite estáticas (momentos de flexión cero). La función shape previamente considerada, Ecuación\ ref {8.3.20} condujo a la curvatura de restricción, lo que significa que se violaron las condiciones de límite estático. Después del cálculo sencillo, el coeficiente numérico se convierte\(\frac{1680}{170} = 9.88\). Hubo más de 20% de mejoras en la precisión de la solución
\[N_c = 9.88 \frac{EI}{l^2} \]
¿Se puede mejorar (bajar) aún más la solución? sí, pero no por mucho. Asumir una forma sinusoidal de la forma de pandeo
\[\phi = \sin \frac{\pi x}{l} \label{8.3.28}\]
\[\phi^{\prime} = \frac{\pi}{l} \cos \frac{\pi x}{l} \]
\[\phi^{\prime\prime} = − \left(\frac{\pi}{l}\right)^2 \sin \frac{\pi x}{l} \label{8.3.30}\]
La expresión de la carga crítica de pandeo se convierte en
\[N_c = \frac{EI(\frac{\pi}{l})^4}{(\frac{\pi}{l})^2} \frac{\int_{0}^{l} \sin^2 \frac{\pi x}{l} dx} {\int_{0}^{l} \cos^2 \frac{\pi x}{l} dx} \]
Ambas integrales son idénticas y la solución se convierte en
\[N_c = \frac{ \pi^2 EI}{l^2} \label{8.3.32}\]
Porque\(\pi^2 = 9.86\), la solución sinusoidal es ligeramente inferior a la solución polinómica anterior. Este es el coeficiente más bajo posible, lo que significa que debe ser una solución exacta al problema de pandeo. Para probarlo, basta con verificar si se cumple la ecuación de equilibrio local
\[EIw^{\mathrm{IV}} + Nw^{\prime\prime} = 0 \]
En efecto, al sustituir las Ecuaciones\ ref {8.3.28} -\ ref {8.3.30} y\ ref {8.3.32} en la ecuación de equilibrio lleva el lado izquierdo de esta ecuación de manera idéntica a cero.


