8.4: Efecto de las Imperfecciones Estructurales
- Page ID
- 85135
Considera el mismo strutter discreto que en la Sección 8.2. Esta vez la varilla rígida no es recta sino que se gira por el ángulo\(\theta_o\) antes de aplicar la carga vertical. Al aplicar la carga la columna se somete a rotación adicional\(\theta\), medida desde la dirección vertical teórica, Figura (\(\PageIndex{1}\)).
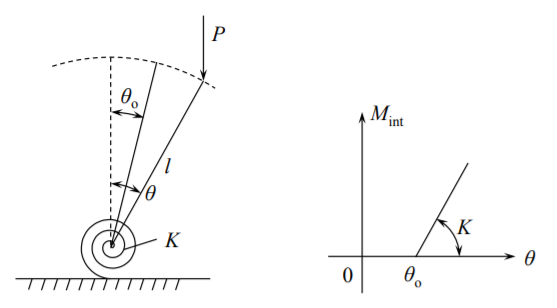
El problema se resolverá mediante el equilibrio local. El momento de flexión externo en la base es
\[M_{\text{ext}} = Pl \sin \theta, \text{ for } \theta \geqslant \theta_o \]
donde\(l \sin \theta\) está el brazo de la fuerza\(P\). En el caso de aproximación de ángulo pequeño\(M_{\text{ext}} = Pl \theta\). El momento de flexión de resistencia interno es
\[M_{\text{int}} = K(\theta − \theta_o) \]
Equiparar los momentos de flexión externos e internos
\[Pl \theta = K(\theta − \theta_o) \label{9.40}\]
Para una columna geométricamente perfecta\(\theta_o = 0\) y de la ecuación\ ref {9.40}
\[P = P_c = \frac{K}{l} \]
La ecuación\ ref {9.40} se puede reescribir en términos de la fuerza de compresión normalizada\(P/P_c\)
\[\frac{P}{P_c} \theta = \theta − \theta_o \]
Resolviendo esta ecuación para\(\theta\) rendimientos
\[\theta = \theta_o \frac{1}{1 − \frac{P}{P_c}} \]
La gráfica de la función anterior se muestra en la Figura (\(\PageIndex{2}\)). El término\(1/(1 − \frac{P}{P_c} )\) se llama el factor de aumento. Predice cuánto se magnifican las imperfecciones iniciales para una determinada magnitud de carga. Cuando las imperfecciones estructurales están presentes, no hay caminos de equilibrio primario y secundario. Solo hay una curva suave de carga-deflexión llamada trayectoria de equilibrio.
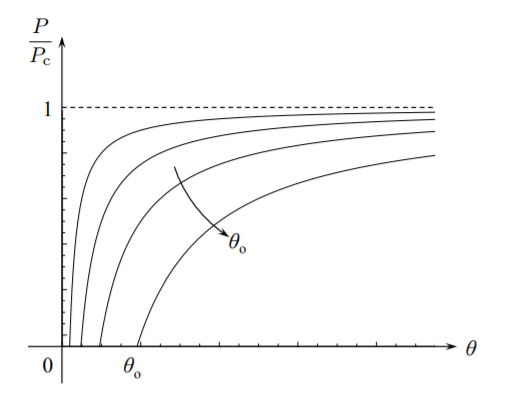
Es interesante señalar que con imperfecciones iniciales cada vez más pequeñas, los caminos de equilibrio se acercan al punto de bifurcación pero nunca lo alcanzan. Este tipo de comportamiento es común a todas las estructuras imperfectas.
Como otro ejemplo de una estructura imperfecta considera una columna elástica de alfiler. Se introduce la siguiente notación:
- \(\bar{w}(x)\)— forma de imperfección inicial
- \(\bar{w}_o\)— amplitud de la imperfección inicial
- \(w(x)\)— forma real de pandeo medida desde la posición vertical (perfecta)
- \(w_o\)— amplitud central de la deflexión real
El momento de flexión interno es
\[M_{\text{int}} = EI \Delta\kappa = −EI(w^{\prime \prime} − \bar{w}^{\prime \prime}) \]
donde\(\Delta\kappa\) es el cambio de curvatura desde la columna curva inicial (imperfecta). Para una columna simplemente soportada, los momentos finales (reacción) son cero, por lo que el momento de flexión externo es
\[M_{\text{ext}} = P w \]
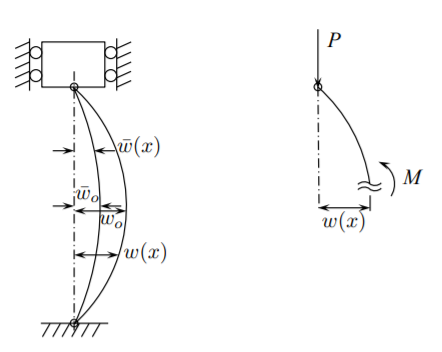
Equiparando los momentos de flexión internos y externos que uno obtiene
\[EIw^{\prime \prime} + P w = EI\bar{w}(x) \label{9.46}\]
Se trata de una ecuación diferencial lineal no homogénea de segundo orden, donde el lado derecho es una forma conocida de imperfección inicial. La solución a esta ecuación existe en términos de cuadraturas, pero las integrales son difíciles de evaluar para formas complejas de imperfecciones.
Consideremos el caso más simple de una forma sinusoidal de imperfecciones. Se puede demostrar que la solución\(w(x)\) es también de la forma sinusoidal
\[w(x) = w_o \sin \lambda x \label{9.47a}\]
\[\bar{w}(x) = \bar{w}_o \sin \lambda x \label{9.47b}\]
Las condiciones de contorno cinemático son
\[w(0) = w(l) = 0 \nonumber\]
lo que implica que
\[\sin \lambda l = 0 \quad \rightarrow \quad \lambda l = n \pi \]
Sustituyendo ecuaciones\ ref {9.47a} -\ ref {9.47b} en la ecuación gobernante\ ref {9.46}
\[−EI \lambda^2 (w_o − \bar{w}_o) \sin \lambda x − P w_o \sin \lambda x = 0 \]
que se satisface si
\[P w_o = EI(w_o − \bar{w}_o) \lambda^2 \label{9.50}\]
Para una columna perfecta\(\bar{w}_o = 0\), y Ecuación\ ref {9.50} rinde
\[(P_c − EI \lambda^2 )w_o = 0 \\ \text{or }P_c = EI\lambda^2 = \frac{n^2 \pi^2 EI}{l^2} \]
Para una columna imperfecta
\[P w_o = P_c(w_o − \bar{w}_o) \]
o resolviendo\(w_o\)
\[w_o = \bar{w}_o \frac{1}{1 − \frac{P}{P_c}} \]
La forma del factor de aumento es idéntica a la derivada para la columna distrital. La única diferencia es que una columna continua tiene modo de pandeo infinito donde\(n = 1\) corresponde a la carga de pandeo más baja. La carga de pandeo correspondiente al segundo modo de pandeo es cuatro veces mayor y así sucesivamente.


