8.5: Estabilidad en Tensión

Para algunos materiales la inestabilidad en la tensión se manifiesta por un desarrollo de un cuello local, Figura (\(\PageIndex{1}\)).

Figura\(\PageIndex{1}\): Reforzamiento en una barra de sección sólida y tubo de pared delgada bajo tensión.

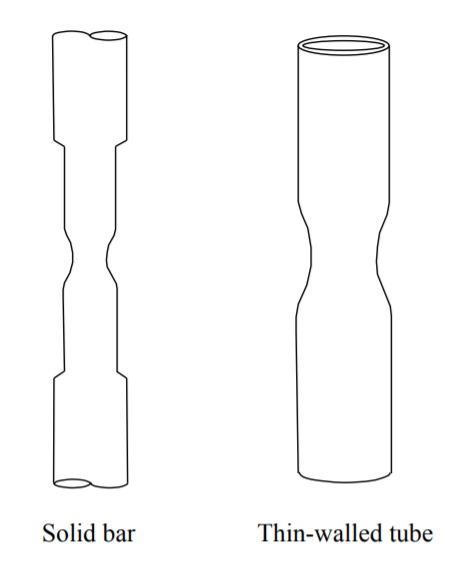
Considere una barra redonda del área de la sección transversal inicial\(A_o\) sometida a una fuerza de tracción\(P\). La barra se alarga y debido al efecto Poisson su sección transversal se contrae a un valor actual\(A\). El presente análisis es válido para materiales que son incompresibles, es decir, no cambian de volumen sino solo de forma. Ciertos polímeros, caucho y metales (en la gama plástica) son incompresibles.

El volumen de una longitud infinitesimal\(l\) es

\[ V = lA \]

El incremento de volumen para el material incompresible debe ser igual a cero

\[\delta V = \delta (lA) = \delta lA + l \delta A = 0 \]

Tome la definición logarítmica de la deformación axial

\[\epsilon = \ln \frac{l}{l_o} ; \quad \delta \epsilon = \frac{\delta l}{l} \]

De las dos ecuaciones anteriores

\[\delta \epsilon = \frac{\delta l}{l}= − \frac{\delta A}{A} \]

Integrando ambos lados

\[\epsilon = − \ln A + C \nonumber\]

En\(A = A_o\),\(\epsilon = 0\) entonces\(C = \ln A_o\).

Por lo tanto, la expresión de la deformación axial se convierte en

\[\epsilon = \ln \frac{A_o}{A} = \ln \frac{l}{l_o} \]

Se concluye que la deformación axial se puede determinar midiendo el cambio de longitud o el cambio en el área de la sección transversal. La tensión verdadera (Cauchy) se define como la carga dividida por la sección transversal actual\(A\)

\[\sigma = \frac{P}{A} \]

Construyamos la energía potencial total y su primera variación

\[\delta \prod = \int_{V} \sigma \delta \epsilon dv − P \delta u \label{9.60}\]

Antes de que ocurra la inestabilidad, la deformación y la tensión (tensión uniaxial) es uniforme a través de la sección de la barra de la longitud\(l\)

\[u = l \epsilon = l \ln \frac{A_o}{A} \label{9.61a}\]

\[\delta u = −l \frac{\delta A}{A} \label{9.61b}\]

Así, de Ecuaciones\ ref {9.60} y\ ref {9.61a} -\ ref {9.61b}

\[\delta \prod = \int_{V} \sigma \delta \epsilon dv + Pl \frac{\delta A}{A} \]

La segunda variación de la energía potencial total es

\[\delta^2 \prod = \int_{V} \delta \sigma \delta \epsilon dv − Pl \frac{\delta A \delta A}{A^2} \]

Aplicando la condición de estabilidad Trefftz\(\delta^2 \prod = 0\) se obtiene

\[lA \delta \sigma \delta \epsilon = Pl \delta \epsilon \delta \epsilon \]

o

\[\delta \sigma = \frac{P}{A} \delta \epsilon = \sigma \delta \epsilon \]

y finalmente

\[ \frac{\delta \sigma}{\delta \epsilon} = \sigma \label{9.66}\]

La barra incompresible está perdiendo estabilidad en tensión cuando la tangente local a la curva tensión-deformación se vuelve igual al valor de la tensión en ese punto. En la Figura (\(\PageIndex{2}\)) se muestra una interpretación gráfica.

Figura\(\PageIndex{2}\): La construcción de Considere' quien fue el primero en derivar la Ecuación\ ref {9.66}.

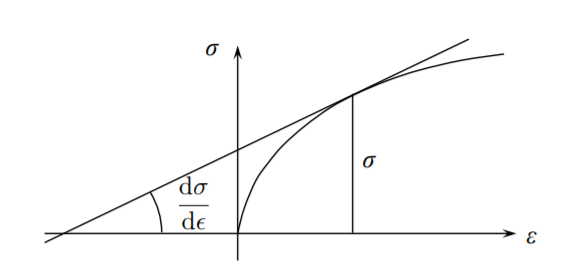
¿A qué tensión se desarrolla una inestabilidad para un material elástico? En tensión uniaxial

\[\sigma = E\epsilon \]

\[\frac{d\sigma}{d\epsilon} = E \]

Ecuación\ ref {9.66} se satisface si\(\epsilon = 1\). Para los metales tal deformación no es alcanzable en el rango elástico porque el rendimiento se alcanzará en la deformación\(\epsilon_y = \frac{\sigma_y}{E} \cong 10^{−3}\). Sin embargo, para el caucho y materiales poliméricos similares el módulo de Young es cuatro órdenes de magnitud menor, por lo que el cuello es de ocurrencia común. La derivación de la condición de inestabilidad\ ref {9.66} se realizó sin ninguna suposición sobre la relación tensión-deformación del material. Por lo tanto esta condición es válida para un material elástico así como plástico. Esto nos lleva al siguiente tema que es el pandeo plástico de columnas.