9.3: Snap-through de un sistema de dos barras

Este es un problema muy interesante, porque resume e incluso extiende nuestros conocimientos.

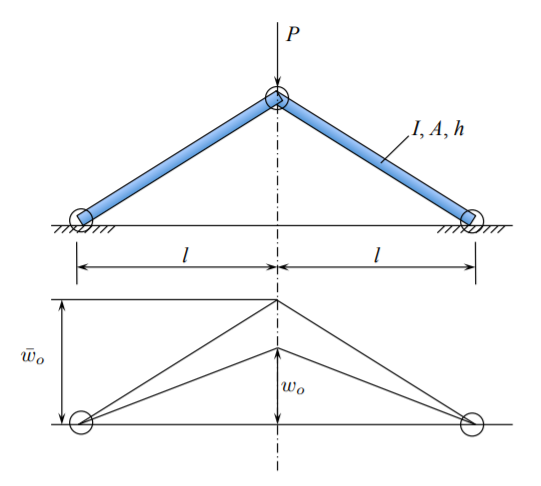
Hay tres bisagras para que cada varilla sea una columna de pasador y pasador. Las varillas son elásticas caracterizadas por la rigidez a la flexión\(EI\), rigidez axial\(EA\). La configuración inicial sin estrés se define por la altura\(\bar{w}_o\), que anteriormente se llamaba la amplitud de la imperfección inicial.

Figura\(\PageIndex{1}\): Relación entre la carga axial y las deflexiones laterales.

Aquí,\(\bar{w}_o\) debe considerarse como la forma inicial de la estructura. Al aplicar la carga, se desarrolla una fuerza axial compresiva en la varilla, su longitud se acorta permitiendo una configuración recta (plana). El sistema encaja en una nueva configuración donde la fuerza de tracción se desarrolla en las varillas. Dependiendo de la relación de esbeltez, pueden doblarse en algún momento durante el proceso de carga.

Solución de prepandeo

Debido a las bisagras inamovibles, los componentes en el plano del desplazamiento es cero,\(u = 0\). La deformación en las barras se desarrolla por la presencia de rotaciones finitas

\[\epsilon = \frac{1}{2} (w^{\prime})^2 − \frac{1}{2}(\bar{w}^{\prime})^2 \label{10.33}\]

En la configuración de prepandeo las varillas son rectas, por lo que

\[w^{\prime} = \frac{w_o}{l}, \quad \bar{w}^{\prime} = \frac{\bar{w}_o}{l} \]

y Ecuación\ ref {10.33} reduce a

\[\epsilon = \frac{1}{2} \left(\frac{w_o}{l}\right)^2 − \frac{1}{2} \left(\frac{\bar{w}_o}{l}\right)^2 \]

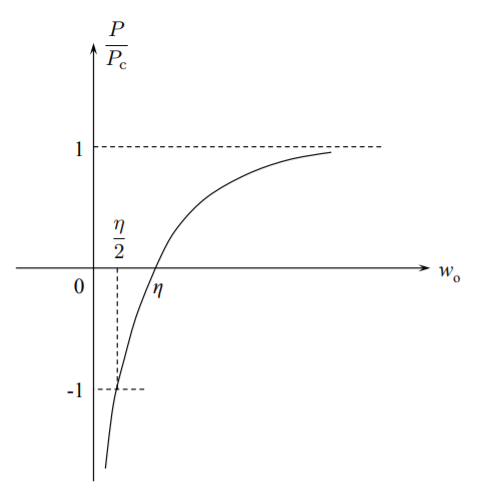
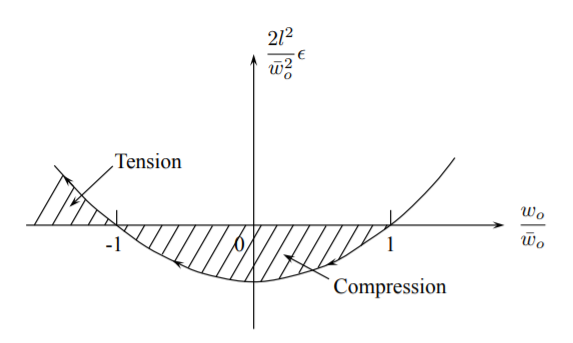
La gráfica de la deformación adimensional versus la relación\(w_o/\bar{w}_o\) se muestra en la Figura (\(\PageIndex{3}\)). De la ley de elasticidad, la fuerza axial en la varilla es

\[N = EA \epsilon = \frac{EA}{2} \left[ \left(\frac{w_o}{l}\right)^2 − \left(\frac{\bar{w}_o}{l}\right)^2 \right] = \begin{cases} \text{compressive for } − w_0 \leqslant w_o \leqslant \bar{w}_o \\ \text{tensile for } w_o < −\bar{w}_o \end{cases} \label{10.36}\]

Figura\(\PageIndex{2}\): Forma inicial y actual del sistema de dos barras.

El equilibrio entre la carga externa\(P\) y la fuerza de membrana\(N\) requiere que

\[P = −2N \frac{w_o}{l} \label{10.37}\]

Eliminando la fuerza\(N\) entre las ecuaciones\ ref {10.36} y\ ref {10.37} rendimientos

\[− \frac{P}{2}\frac{l}{w_o} = EA \left[ \frac{1}{2} \left(\frac{w_o}{l}\right)^2 − \frac{1}{2} \left(\frac{\bar{w}_o}{l}\right)^2 \right]\]

o en una forma adimensional

\[\bar{P} = \delta(\bar{\delta}^2 − \delta^2) \label{10.39}\]

donde

\[\bar{P} = \frac{P}{EA}, \quad \delta = \frac{w_o}{l}, \quad \bar{\delta} = \frac{\bar{w}_o}{l} \]

El camino de equilibrio dado por la Ecuación\ ref {10.39} es la parábola de tercer orden con tres raíces en\(\delta = 0, \delta = \pm \bar{\delta}\), ver Figura (\(\PageIndex{4}\)).

El proceso de carga comienza en A y la porción de la trayectoria AB es estable. El punto B es el punto de inestabilidad. En el proceso se controla la fuerza, hay un salto a la siguiente configuración de equilibrio que es el punto E. Entonces el sistema “encaja” en una configuración de tracción y esta transición es en realidad un problema dinámico. El proceso puede ser control de desplazamiento y luego la fuerza\(\bar{P}\) es la fuerza de reacción que es positiva en los segmentos ABC y EF pero negativa en el segmento CDE de la trayectoria. Esto significa que\(\bar{P}\) se requiere una fuerza opuesta en CDE para mantener el sistema en equilibrio estático. Por el contrario, en el proceso de fuerza controlada la fuerza de inercia está equilibrando el sistema en cualquier momento. La fuerza máxima ocurre cuando

\[\frac{dP}{d\delta} = \bar{\delta}^2 − 3\delta^2 = 0 \]

Figura\(\PageIndex{3}\): Transición de compresión a deformación por tracción.

Figura\(\PageIndex{4}\): Trayectoria de equilibrio en el problema de snap-through.

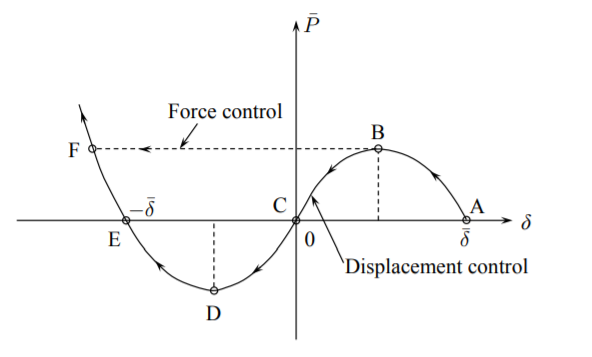
El máximo ocurre en\(\delta = \bar{\delta}/\sqrt{3}\) y la fuerza máxima es\(\bar{P}_{\text{max}} = \frac{2}{3 \sqrt{3}} \bar{\delta}^3\).

En cualquier momento durante la fase de carga AB existe la posibilidad de que las varillas se doblen. El instante de pandeo se detecta igualando la fuerza axial de la Ecuación (10.37) a la fuerza crítica de pandeo de la columna de pasador y pasador

\[N = \frac{P_{cr}}{2}\frac{l}{w_o} = \frac{\pi^2 EI}{l^2} \label{10.42}\]

La versión adimensional de esta ecuación es

\[\bar{P}_{cr} = \frac{P_{cr}}{EA} = 2\pi^2 \frac{\delta}{\beta^2} \]

donde\(\beta = \frac{l}{r}\) está la relación de esbeltez, y\(r^2 = \frac{I}{A}\) es el radio de giro de la sección transversal. En el sistema de coordenadas\((\bar{P}, \delta)\), el punto de pandeo está determinado por la intersección de la línea recta, Ecuación\ ref {10.42}, y la parábola de tercer orden

\[\frac{2\pi^2}{\beta^2}\delta = \delta(\bar{\delta}^2 − \delta^2_c ) \]

El desplazamiento a la hebilla es

\[\delta_c = \sqrt{\bar{\delta}^2 − \frac{2\pi^2}{\beta^2}} \]

y la fuerza de pandeo correspondiente\(\bar{P}_c\) es

\[\bar{P}_c = \frac{2\pi^2}{\beta^2} \sqrt{ \bar{\delta}^2 − \frac{2\pi^2}{\beta^2}} \]

La interpretación gráfica del análisis anterior se muestra en la Figura (\(\PageIndex{5}\)).

Figura\(\PageIndex{5}\): La trayectoria de prepandeo no lineal se cruza con una trayectoria lineal posterior al pandeo.

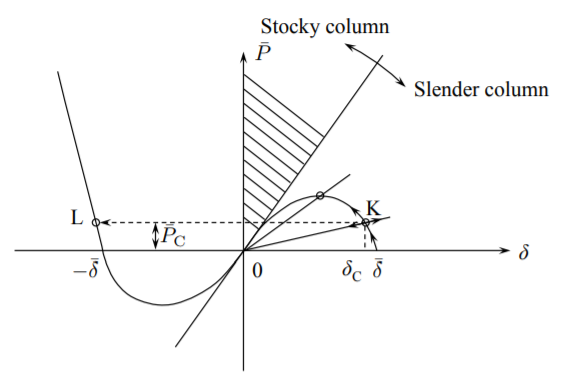
Existe una familia de líneas rectas con la relación de esbeltez como parámetro. La relación crítica de esbeltez para la cual el pandeo nunca ocurrirá es

\[\beta^2_{cr} = \frac{2\pi}{\bar{\delta}} \]

Esta situación corresponde a la línea recta tangente a la parábola de tercer orden. De interés práctico es la situación en la que se produce el punto de bifurcación antes de que se alcance la fuerza máxima en\(\delta_{\text{max}} = \bar{\delta}/\sqrt{3}\) y\(\bar{P}_{\text{max}} = \frac{2}{3 \sqrt{3}}\bar{\delta}^3\). La relación mínima de esbeltez correspondiente, calculada a partir de la Ecuación\ ref {10.42} es

\[\beta_{\text{min}}^2 = \frac{\sqrt{3} \pi}{\bar{\delta}} \]

En resumen, hay tres rangos de la relación de esbeltez:

Tabla\(\PageIndex{1}\): Intervalos de respuesta al pandeo

	\(\beta_{\text{min}} < \beta < \infty\)	\(\beta = \beta_{\text{min}}\)	\(\beta = \beta_{\text{min}}\)
\(\bar{P}_{\text{max}}\)		\(\frac{2}{3\sqrt{3}}\bar{\delta}^3\)	\ (\ beta =\ beta_ {\ text {min}}\) ">Sin pandeo de ruta de equilibrio estático o dinámico
\(\delta_{\text{max}}\)		\(\frac{\bar{\delta}}{\sqrt{3}}\)	\ (\ beta =\ beta_ {\ text {min}}\) ">Sin pandeo de ruta de equilibrio estático o dinámico

Para la sección transversal cuadrada\(h \times h\), la combinación crítica de los parámetros geométricos

\[\frac{\bar{w}_o}{h} = 36 \pi \frac{h}{l}\]

De la solución anterior, concluimos que el snap-through del sistema de barras sin pandeo ocurrirá solo para sistemas muy poco profundos.