9.4: Snap-Through dinámico

Las notas de la presente conferencia están restringidas a problemas estáticos y cuasiestáticos. Sin embargo, la naturaleza del problema del snap-through requiere la consideración del análisis dinámico completo. Supongamos que la carga del sistema de dos barras está controlada por carga. Hay una trayectoria de equilibrio estable en la porción AB. Cuando\(\bar{P}_{\text{max}} = \frac{2}{3 \sqrt{3}}\bar{\delta}^3\) se alcanza, el sistema salta instantáneamente al siguiente punto de equilibrio F en la solución estática. La magnitud de la fuerza es la misma, pero el desplazamiento correspondiente se determina a partir de la solución de la ecuación cúbica

\[\frac{2}{3\sqrt{3}}\bar{\delta}^3 = \delta \bar{\delta}^2 − \delta^3 \]

Esta ecuación tiene tres raíces reales

\[\delta_1 = \frac{\bar{\delta}}{\sqrt{3}}, \delta_2 = \delta_3 = − \frac{2 \bar{\delta}}{\sqrt{3}} \]

Al agregar fuerzas de inercia a la ecuación de equilibrio, el proceso de salto se produce en el tiempo. El sistema de barras se acelera primero en la porción BCD de la fuerza descendente y luego se desacelera en la porción ascendente DEF.

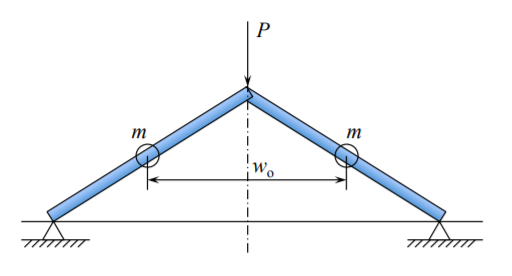
La solución dinámica es sencilla si la masa distribuida de la varilla es agrupada en dos masas puntuales discretas\(m = lA\rho\), como se muestra en la Figura (\(\PageIndex{1}\)).

Al agregar fuerzas de inercia de d'Alambert al equilibrio estático, Ecuación (9.3.5), se obtiene

\[−P − 2m \frac{\ddot{w}_o}{2} = 2N \frac{w_o}{l} \label{10.52}\]

donde ahora\(P\) es positivo en tensión.

Figura\(\PageIndex{1}\): El equivalente de dos barras sin masa y dos masas agrupadas.

Eliminando la fuerza axial\(N\) en las barras entre las ecuaciones (9.3.4) y\ ref {10.52}, se obtiene la siguiente ecuación diferencial

\[−\bar{P} − \frac{l^2 \rho}{E} \ddot{\delta} = \delta [ \delta^2 − \bar{\delta}^2 ] \label{10.53}\]

donde el punto denota diferenciación con respecto al tiempo. Es conveniente introducir el tiempo adimensional\(\bar{t} = \frac{t}{t_1}\), donde\(t_1 = \frac{l}{c}\) está el tiempo de referencia, y\(c^2 = \frac{E}{\rho}\) es la velocidad de la onda de esfuerzo longitudinal en una barra. En el sistema de fuerza controlada, el término emocionante es constante\(\bar{P} = \frac{2}{3 \sqrt{3}}\bar{\delta}^3\). En la nueva coordenada adimensional, la Ecuación\ ref {10.53} toma la forma

\[−\bar{P} − \ddot{\delta} = \delta^3 − \bar{\delta}^2 \delta \label{10.54}\]

donde el punto denota diferenciación con respecto al tiempo adimensional\(\bar{t}\). Utilizando la regla de la diferenciación en cadena,

\[\ddot{\delta} = \frac{d \dot{\delta}}{d\bar{t}} = \frac{d \dot{\delta}}{d\delta} \frac{d \delta}{d\bar{t}} = \frac{d \dot{\delta}}{d\delta} \dot{\delta} \label{10.55}\]

se puede obtener una solución en el plano de fase\((\delta, \dot{\delta}\)) más bien bronceada en el dominio del tiempo. Sustituyendo la ecuación\ ref {10.55} en la ecuación\ ref {10.54}, se obtiene la siguiente ecuación

\[−\bar{P} d\delta − \dot{\delta}d \dot{\delta} = (\delta^3 − \bar{\delta}^2 \delta ) d\delta \]

que se puede integrar fácilmente para dar

\[−\bar{P} \delta − \frac{1}{2} \dot{\delta}^2 = \frac{\delta^4}{4} − \frac{\bar{\delta^2}\delta^2}{2} + C \label{10.57}\]

La constante de integración\(C\) se determina a partir de la condición inicial de que la velocidad\(\dot{\delta}\) es cero cuando la deflexión alcanza\(\delta = \frac{1}{\sqrt{3}}\) (punto B). La solución para la velocidad\(\dot{\delta}\) es

\[\dot{\delta} = 2\bar{\delta}^2 \sqrt{−P \left(\frac{\delta}{\bar{\delta}}\right) + \frac{1}{2}\left(\frac{\delta}{\bar{\delta}}\right)^2 − \frac{1}{4} \left(\frac{\delta}{\bar{\delta}}\right)^4 + \frac{1}{12}} \label{10.58}\]

En términos de la velocidad normalizada\(\frac{\dot{\delta}}{2 \bar{\delta}^2} = \bar{v}\) y la deflexión normalizada\(\eta = \frac{\delta}{\bar{\delta}}\), la ecuación\ ref {10.58} lee

\[\bar{v} = \sqrt{−\frac{2}{3 \sqrt{3}}\eta + \frac{1}{2}\eta^2 − \frac{1}{4}\eta^4 + \frac{1}{12}} \label{10.59}\]

La gráfica de\(\bar{v}\) versus\(\eta\) se muestra en la Figura (\(\PageIndex{2}\)).

Figura\(\PageIndex{2}\): La gráfica de\(\bar{v}\) versus\(\eta\) en snap through dinámico.

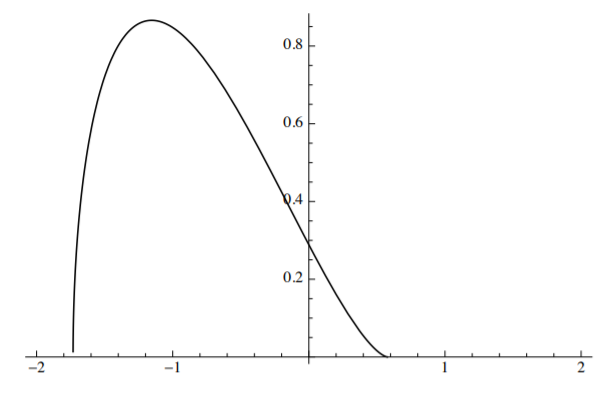
El polinomio en\(\eta\) debajo de la raíz cuadrada en la Ecuación\ ref {10.59} tiene dos raíces reales, at\(\eta = \frac{1}{\sqrt{3}}\) y\(\eta = − \sqrt{3}\). El movimiento dinámico comienza en B, aumenta lentamente, alcanza un máximo en F y cae rápidamente a cero en el punto G con la coordenada\(\eta_f = \sqrt{3}\). Tenga en cuenta que la deflexión dinámica sobrepasa considerablemente la deflexión alcanzada en el problema estático\(\eta_{\text{stat}} = \frac{2}{\sqrt{3}} = 1.15\).

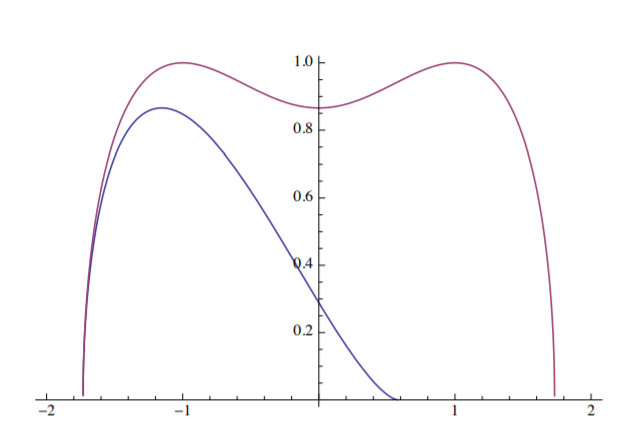
En la etapa final cuando el movimiento del sistema se detiene, hay suficiente energía de tracción almacenada en la barra para iniciar la vibración libre con el término de forzamiento\(\bar{P}\) eliminado. La solución a esta fase viene dada por la Ecuación\ ref {10.57} con\(\bar{P} = 0\), y la nueva constante de integración\(C_1 = \frac{3}{4}\) para que se logre continuidad de velocidad. La trama de la vibración libre del sistema, gobernada por

\[\bar{v} = \sqrt{\frac{1}{2}\eta^2 − \frac{1}{4}\eta^4 + \frac{3}{4}} \]

se muestra en la Figura (\(\PageIndex{3}\)), en comparación con la gráfica dinámica de snap-through.

Figura\(\PageIndex{3}\): La gráfica de\(\bar{v}\) versus\(\eta\) en vibración libre, en comparación con la gráfica dinámica pasante.