2.3: Cizalla y Torsión
- Page ID
- 83353
Introducción
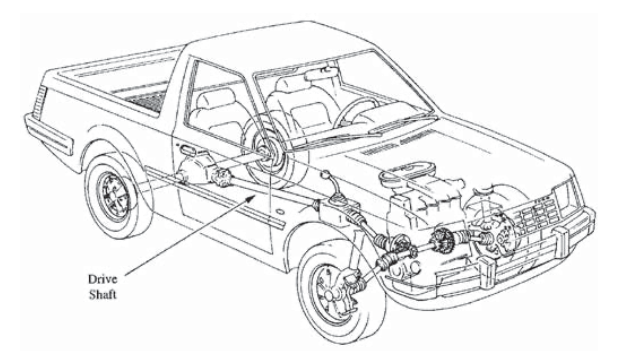
Los ejes cargados torsionalmente se encuentran entre las estructuras más utilizadas en ingeniería. Por ejemplo, el eje de transmisión de un automóvil de tracción trasera estándar, representado en la Figura 1, sirve principalmente para transmitir torsión. Estos ejes son casi siempre huecos y circulares en sección transversal, transmitiendo potencia desde la transmisión a la junta diferencial en la que se desvía la rotación hacia las ruedas motrices. Al igual que en el caso de los recipientes a presión, es importante conocer los métodos de diseño para tales estructuras puramente por su utilidad inherente. Sin embargo, los estudiamos aquí también porque ilustran el papel de las tensiones y deformaciones de cizallamiento.
Tensiones y deformaciones por cizallamiento
No toda la deformación es elongacional o compresiva, y necesitamos extender nuestro concepto de deformación para incluir efectos de “cizallamiento” o “distorsión”. Para ilustrar la naturaleza de las distorsiones por cizallamiento, primero considere una rejilla cuadrada inscrita en una muestra de tracción como se representa en la Figura 2 (a). Tras la carga uniaxial, la rejilla se deformaría para aumentar la longitud de las líneas en la dirección de carga de tracción y contraer las líneas perpendiculares a la dirección de carga. Sin embargo, las líneas permanecen perpendiculares entre sí. Estas se denominan deformaciones normales, ya que los planos normales a la dirección de carga se están separando.
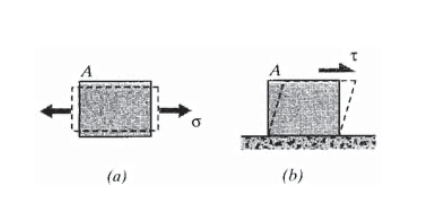
Consideremos ahora el caso ilustrado en la Figura 2 (b), en el que la carga\(P\) se aplica transversalmente al espécimen. Aquí las líneas horizontales tienden a deslizarse una respecto a la otra, permaneciendo inalteradas las longitudes de línea de la cuadrícula originalmente cuadrada. Las líneas verticales se inclinan para acomodar este movimiento, por lo que los ángulos originalmente rectos entre las líneas se distorsionan. Tal carga se conoce como cizallamiento directo. Análogamente a nuestra definición de tensión normal como fuerza por unidad de área (Ver Módulo 1, Introducción a la Respuesta Elástica), o bien\(\sigma = P/A\), escribimos la tensión cortante\(\tau\) como
\[\tau = \dfrac{P}{A}\nonumber\]
Esta expresión es idéntica a la expresión para estrés normal, pero el símbolo diferente nos\(\tau\) recuerda que la carga es transversal más que extensional.
Ejemplo\(\PageIndex{1}\)
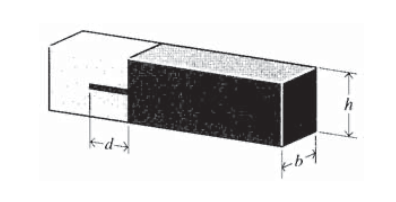
Dos maderas, de dimensión transversal\(b \times h\), se van a pegar entre sí utilizando una unión machihembrada como se muestra en la Figura 3, y se desea estimar la profundidad\(d\) de la junta de pegamento para que la junta sea aproximadamente tan fuerte como la propia madera.
La carga axial\(P\) sobre la madera actúa para cortar la junta de pegamento, y el esfuerzo cortante en la junta es solo la carga dividida por el área total de pegamento:
\[\tau = \dfrac{P}{2bd}\nonumber\]
Si la unión falla cuando\(\tau\) alcanza un valor máximo\(\tau_f\), la carga al fallar será\(P_f = (2bd) \tau_f\). La carga necesaria para fracturar la madera en tensión es\(P_f = bh \sigma_f\), donde\(\sigma_f\) está la máxima resistencia a la tracción de la madera. De ahí que si la junta de pegamento y la madera van a ser igualmente fuertes tenemos
\[(2bd) \tau_f = bh\sigma_f \to d = \dfrac{h\sigma_f}{2\tau_f}\nonumber\]
Las tensiones normales actúan para separar planos paralelos dentro del material o empujarlos más cerca, mientras que los esfuerzos cortantes actúan para deslizar planos uno a lo largo del otro. Las tensiones normales promueven la formación y crecimiento de grietas, mientras que las tensiones cortantes subyacen al rendimiento y al deslizamiento plástico. El esfuerzo cortante se puede representar en el cuadrado de tensión como se muestra en la Figura 4 (a); es tradicional usar una media punta de flecha para distinguir el esfuerzo cortante de la tensión normal. El\(yx\) subíndice indica que la tensión está en el\(y\) plano en la\(x\) dirección.

La\(\tau_{yx}\) flecha en el\(+y\) plano debe ir acompañada de una en sentido contrario en el\(-y\) plano, para mantener el equilibrio horizontal. Pero estas dos flechas por sí mismas tenderían a provocar una rotación en sentido horario, y para mantener el equilibrio de momento también debemos agregar dos flechas verticales como se muestra en la Figura 4 (b); estas están etiquetadas\(\tau_{xy}\), ya que están en\(x\) planos en la dirección y. Para el equilibrio rotacional, las magnitudes de las tensiones horizontal y vertical deben ser iguales:
\[\tau_{yx} = \tau_{xy}\]
Por lo tanto, cualquier cizallamiento que tiende a causar deslizamiento tangencial de planos horizontales se acompaña de una tendencia igual a deslizarse planos verticales también. Tenga en cuenta que todos estos son positivos por nuestra convención anterior de + flechas en + caras siendo positivas. Un estado positivo de esfuerzo cortante, entonces, tiene flechas que se encuentran en la parte superior derecha e inferior izquierda del cuadrado de tensión. Por el contrario, las flechas en estado negativo de cizallamiento se encuentran en la parte inferior derecha y superior izquierda.
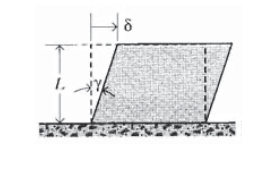
La deformación que acompaña al esfuerzo cortante\(\tau_{xy}\) es una deformación cortante denotada\(\gamma_{xy}\). Esta cantidad es una deformación por unidad de longitud igual que lo fue la deformación normal\(\epsilon\), pero ahora el desplazamiento es transversal a la longitud sobre la que se distribuye (ver Figura 5). Esta es también la distorsión o cambio en el ángulo recto:
\[\dfrac{\delta}{L} = \tan \gamma \approx \gamma\]
Se encuentra experimentalmente que esta distorsión angular es linealmente proporcional al esfuerzo cortante a cargas suficientemente pequeñas, y la contraparte de cizallamiento de la Ley de Hooke puede escribirse como
\[\tau_{xy} = G\gamma_{xy}\]
donde\(G\) es una propiedad del material llamada módulo de cizallamiento. para materiales isotrópicos (propiedades iguales en todas las direcciones), no hay ningún efecto de tipo Poisson a considerar en el cizallamiento, por lo que la tensión de cizallamiento no está influenciada por la presencia de tensiones normales. De igual manera, la aplicación de una tensión de cizallamiento no influye en las deformaciones normales. Para situaciones de tensión plana (sin componentes de tensión normal o de cizallamiento en la\(z\) dirección), las ecuaciones constitutivas desarrolladas hasta ahora se pueden escribir:
\[\begin{array} {c} {\epsilon_x = \dfrac{1}{E} (\sigma_x - \nu \sigma_y)} \\ {\epsilon_y = \dfrac{1}{E} (\sigma_y - \nu \sigma_x)} \\ {\gamma_{xy} = \dfrac{1}{G} \tau_{xy}} \end{array}\]
Se mostrará más adelante que para los materiales isotrópicos, solo dos de las constantes materiales aquí son independientes, y que
\[G = \dfrac{E}{2(1 + \nu)}\]
De ahí que si dos cualesquiera de las tres propiedades\(E, G\), o\(\nu\), son conocidas, se determina la otra.
Estáticas - Momentos de Torsión
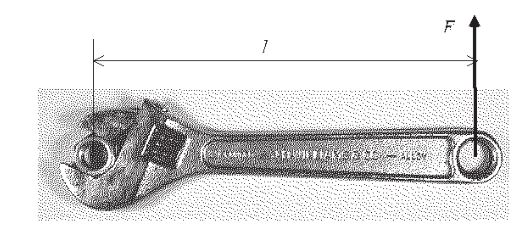
Los momentos de torsión, o pares, son fuerzas que actúan a través de distancias (“brazos de palanca”) para una rotación pro- mota. El ejemplo sencillo es el de usar una llave para apretar una tuerca en un perno como se muestra en la Figura 6: si el perno, la llave y la fuerza son todos perpendiculares entre sí, el momento es solo la fuerza F veces la longitud l de la llave:\(T = F \cdot l\). Esta relación bastará cuando la geometría de la carga torsional sea simple como en este caso, cuando el par se aplique “recto”.
A menudo, sin embargo, la geometría del momento aplicado es un poco más complicada. Considere un caso no infrecuente en el que, por ejemplo, se debe aflojar una bujía y simplemente no hay espacio para ponerle una llave correctamente. Aquí podría ser necesaria una llave de enchufe girada, lo que puede resultar en que el brazo de la palanca no sea perpendicular al eje de la bujía, y la fuerza aplicada (de su mano) no sea perpendicular al brazo de la palanca. El álgebra vectorial puede facilitar los cálculos geométricos en tales casos. Aquí\(O\) se obtiene el vector de momento alrededor de un punto cruzando la representación vectorial del brazo de palanca\(r\) a partir\(O\) del vector de fuerza\(F\):
\[T = r \times F\]
Este vector está en una dirección dada por la regla de la derecha, y es normal al plano que contiene el punto\(O\) y el vector de fuerza. El par que tiende a aflojar la bujía es entonces el componente de este vector de momento a lo largo del eje de la bujía:
\[T = i \cdot (r \times F)\]
donde\(i\) es un vector unitario a lo largo del eje. El resultado, un par o momento de torsión alrededor de un eje, es una cantidad escalar.
Ejemplo\(\PageIndex{2}\)
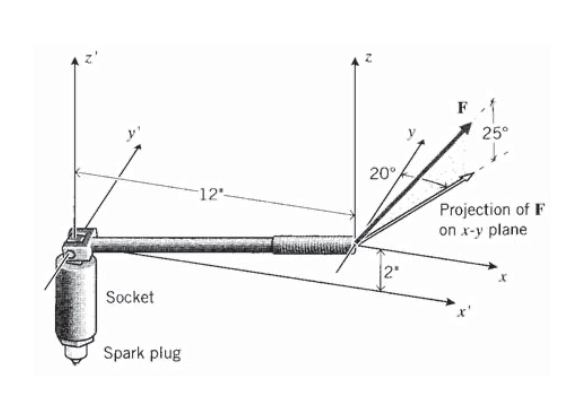
Deseamos encontrar el momento de torsión efectivo en una bujía, donde se aplica la fuerza a una llave giratoria que está sesgada alejándose del eje de la bujía como se muestra en la Figura 7. Se establece un sistema de coordenadas\(x'y'z'\) cartesianas\(z'\) siendo el eje de la bujía; el extremo libre de la llave está\(2''\) por encima del\(x'y'\) plano perpendicular al eje de la bujía, y\(12''\) lejos de la bujía a lo largo del\(x'\) eje. Se aplica una fuerza de 15 lb al extremo libre en un ángulo sesgado de 25\(^{\circ}\) verticales y 20\(^{\circ}\) horizontales.
El vector de fuerza aplicado al extremo libre de la llave es
\[F = 15 (\cos 25 \sin 20 i + \cos 25 \cos 20 j + \sin 25 k)\nonumber\]
El vector desde el eje de rotación hasta la fuerza aplicada es
\[r = 12 i + 0j + 2k \nonumber\]
donde\(i,j,k\), son los vectores unitarios a lo largo de los\(x, y, z\) ejes. El vector momento alrededor del punto\(O\) es entonces
\[T_O = r\times F = (-25.55 i - 66.77j + 153.3k)\nonumber\]
y el momento escalar a lo largo del eje\(z'\) es
\[T_{z'} = k \cdot (r \times F) = 153.3 \ in - lb\nonumber\]
Este es el par que aflojará la bujía, si tienes más suerte que yo con los autos.
Los ejes en torsión se utilizan en casi toda la maquinaria giratoria, como en nuestro ejemplo anterior de un eje de transmisión que transmite el par de un motor de automóvil a las ruedas. Cuando la cabina está operando a velocidad constante (no acelerando), el par en un eje está relacionado con su velocidad de rotación\(\omega\) y la potencia\(W\) que se transmite:
\[W = T \omega\]
Las transmisiones engranadas suelen ser necesarias para mantener la velocidad del motor en límites razonables a medida que el automóvil acelera, y el engranaje debe considerarse al determinar los pares aplicados a los ejes.
Ejemplo\(\PageIndex{3}\)
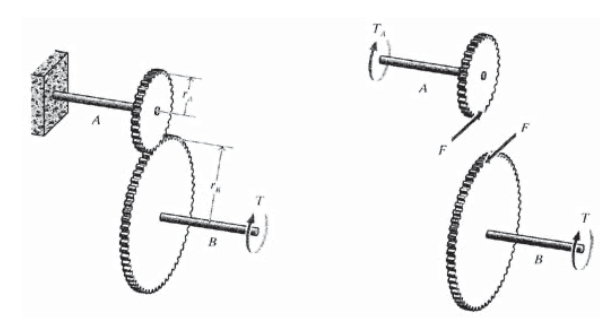
Considere un engranaje simple de dos ejes como se muestra en la Figura 8, con un extremo del eje\(A\) sujeto y el extremo libre del eje\(B\) cargado con un momento\(T\). Dibujando diagramas de cuerpo libre para los dos ejes por separado, vemos que la fuerza\(F\) transmitida en la periferia del engranaje es solo la que mantiene al eje\(B\) en equilibrio rotacional:
\[F \cdot r_B = T\nonumber\]
Esta misma fuerza actúa sobre la periferia del engranaje\(A\), por lo que el par\(T_A\) experimentado por el eje\(A\) es
\[T_A = F \cdot r_A = T \cdot \dfrac{r_A}{r_B}\nonumber\]
Tensiones y Desplazamientos Torsionales
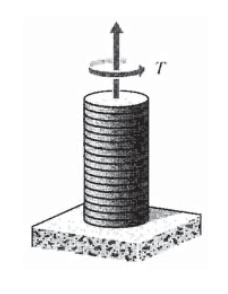
Las tensiones y deformaciones inducidas en un eje circular por un momento de torsión se pueden encontrar por lo que a veces se llama el método directo de análisis de tensiones. Aquí se propone una expresión de la forma geométrica de desplazamiento en la estructura, después de lo cual se aplican secuencialmente las ecuaciones cinemática, constitutiva y de equilibrio para desarrollar expresiones para las tensiones y tensiones. En el caso de la simple torsión de un eje circular, la afirmación geométrica es simplemente que se mantiene la simetría circular del eje, lo que implica a su vez que las secciones transversales planas permanezcan planas, sin deformarse. Como se representa en la Figura 9, la deformación es como una pila de fichas de póquer que giran una respecto a la otra mientras permanecen planas. La secuencia de análisis directo toma entonces la siguiente forma:
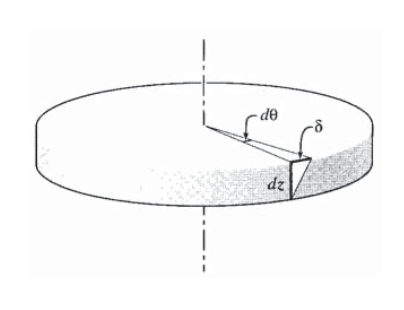
1. Declaración geométrica: Para cuantificar la geometría de la deformación, considere un incremento de longitud\(dz\) desde el eje como se ve en la Figura 10, en la que la parte superior gira con relación a la parte inferior en un incremento de ángulo\(d\theta\). El desplazamiento tangencial relativo de la parte superior de una línea vertical dibujada a una\(r\) distancia del centro es entonces:
\[\delta = r\ d\theta\]
2. Ecuación cinemática o deformación-desplazamiento: La geometría de la deformación se ajusta exactamente a nuestra descripción anterior de la deformación por cizallamiento, por lo que podemos escribir:
\[\gamma_{z\theta} = \dfrac{\delta}{dz} = r \dfrac{d\theta}{dz}\]
El subíndice indica un cizallamiento del\(z\) plano (el plano normal al\(z\) eje) en la\(\theta\) dirección. Al igual que con las tensiones cortantes,\(\gamma_{z\theta} = \gamma_{\theta z}\), por lo que el orden de los subíndices es arbitrario.
3. Ecuación constitutiva: Si el material está en su régimen elástico lineal, el esfuerzo cortante se da directamente de la Ley de Hooke como:
\[\tau_{\theta z} = G\gamma_{\theta z} = Gr\dfrac{d \theta}{dz}\]
La convención de signos aquí es que los momentos de torsión positivos (vector de momento a lo largo del\(z\) eje +) producen tensiones y tensiones de cizallamiento positivas. Sin embargo, probablemente sea más fácil simplemente intuir en qué dirección el momento aplicado tenderá a deslizarse planos horizontales adyacentes. Aquí el plano superior (+\(z\)) se está torciendo claramente hacia la derecha con relación al plano inferior (-\(z\)), por lo que la flecha superior apunta hacia la derecha. Luego se determinan también las otras tres flechas.
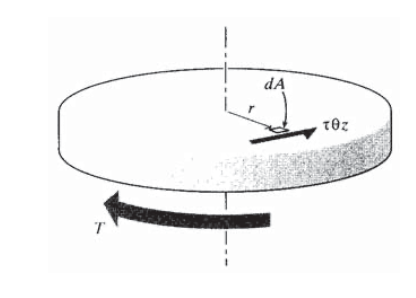
4. 4. Ecuación de equilibrio: Para mantener el equilibrio rotacional, la suma de los momentos aportados por el esfuerzo cortante que actúa sobre cada área diferencial\(dA\) en la sección transversal debe equilibrar el momento aplicado\(T\) como se muestra en la Figura 11:
\[T = \int_A \tau_{\theta z} r dA = \int_A Gr \dfrac{d\theta}{dz} rdA = G \dfrac{d \theta}{dz} \int_A r^2 d A\nonumber\]
La cantidad\(\int r^2 dA\) es el momento polar de inercia\(J\), que para una sección transversal circular hueca se calcula como
\[J = \int_{R_i}^{R_o} r^2 2\pi r dr = \dfrac{\pi (R_o^4 - R_i^4)}{2}\]
donde\(R_i\) y\(R_o\) son los radios interior y exterior. Para ejes sólidos,\(R_i = 0\). La cantidad ahora se\(d \theta /dz\) puede encontrar como
\[\dfrac{d\theta}{dz} = \dfrac{T}{GJ} \to \theta = \int_z \dfrac{T}{JG} dz\nonumber\]
Dado que en el caso de torsión simple bajo consideración las cantidades\(T,J,G\) son constantes a lo largo\(z\), el ángulo de giro se puede escribir como
\[\dfrac{d\theta}{dz} = \text{constant} = \dfrac{\theta}{L}\nonumber\]
\[\theta = \dfrac{TL}{GJ}\]
Esto es análogo a la expresión\(\delta = PL/AE\) para el alargamiento de una muestra de tracción uniaxial.
5. Se puede obtener una fórmula explícita para el estrés usando esto en la Ecuación 2.3.11:
\[\tau_{\theta z} = Gr \dfrac{d\theta}{dz} = Gr \dfrac{\theta}{L} = \dfrac{Gr}{L} \dfrac{TL}{GJ}\nonumber\]
\[\tau_{\theta z} = \dfrac{Tr}{J}\]
Tenga en cuenta que la propiedad material\(G\) ha cancelado de esta expresión final por estrés, de manera que las tensiones son independientes de la elección del material. Anteriormente, hemos observado que las tensiones son independientes de las propiedades de los materiales en ciertos recipientes a presión y elementos de celosía, y esto se debió a que esas estructuras estaban determinadas estáticamente. El eje en torsión no es estáticamente indeterminado, sin embargo; tuvimos que utilizar consideraciones geométricas y una declaración de respuesta elástica lineal material así como equilibrio estático para obtener el resultado. Dado que las propiedades del material no aparecen en la ecuación resultante para la tensión, es fácil olvidar que la derivación dependía de la linealidad geométrica y material. Siempre es importante tener en cuenta los supuestos utilizados en derivaciones como esta, y estar en guardia contra el uso del resultado en instancias para las que los supuestos no están justificados.
Por ejemplo, podríamos torcer un eje hasta que se rompa a un par final de\(T = T_f\), y luego usar la Ecuación 2.3.14 para calcular una resistencia aparente al cizallamiento final:\(\tau_f = T_f r/J\). Sin embargo, el material puede muy bien haber sido estresado más allá de su límite elástico en esta prueba, y la suposición de linealidad del material puede no haber sido válida en caso de falla. El valor resultante de\(\tau_f\) obtenido del análisis elástico es, por lo tanto, ficticio a menos que se demuestre lo contrario, y podría ser sustancialmente diferente a la tensión real. El valor ficticio podría ser utilizado, sin embargo, para estimar pares de falla en ejes del mismo material pero de diferentes tamaños, ya que la tensión de falla real escalaría con la tensión ficticia en ese caso. El esfuerzo de falla ficticio calculado mediante el análisis elástico a menudo se denomina módulo de ruptura en torsión.
La ecuación 2.3.14 muestra una razón por la cual la mayoría de los ejes de transmisión son huecos, ya que no tiene mucho sentido usar material en el centro donde las tensiones son cero. Además, para una determinada cantidad de material el diseñador querrá maximizar el momento de inercia colocando el material lo más lejos posible del centro. Esta es una herramienta potente, ya que J varía como la cuarta potencia del radio.
Ejemplo\(\PageIndex{4}\)
Un motor de automóvil está entregando 100 hp (caballos de fuerza) a 1800 rpm (revoluciones por minuto) al eje de transmisión, y deseamos calcular el esfuerzo de corte. De la Ecuación 2.3.8, el par en el eje es
\[T = \dfrac{W}{\omega} = \dfrac{100\ hp (\tfrac{1}{1.341 \times 10^{-3}})\tfrac{N \cdot m}{s \cdot hp}}{1800 \tfrac{rev}{min} 2\pi \tfrac{rad}{rev} (\tfrac{1}{60}) \tfrac{min}{s}} = 396 N \cdot m\nonumber\]
El presente eje de transmisión es una varilla sólida con una sección transversal circular y un diámetro de\(d = 10\) mm. Usando la Ecuación 2.3.14, la tensión máxima ocurre en la superficie exterior de la varilla tal como está
\[\tau_{\theta z} = \dfrac{Tr}{J}, r = d/2, J = \pi (d/2)^4/2\nonumber\]
\[\tau_{\theta z} = 252 \text{ MPa}\nonumber\]
Ahora considere cuál sería el esfuerzo cortante si el eje se hiciera anular en lugar de sólido, manteniendo igual la cantidad de material. El esfuerzo cortante de la superficie exterior para un eje anular con radio exterior\(r_o\) y radio interior\(r_i\) es
\[\tau_{\theta z} = \dfrac{T_{r_o}}{J}, J = \dfrac{\pi}{2} (r_o^4 - r_i^4)\nonumber\]
Para mantener la cantidad de material en el eje anular igual que en el sólido, las áreas de sección transversal deben ser las mismas. Dado que el área de la sección transversal del eje sólido es\(A_0 = \pi r^2\), el radio interior\(r_i\) de un eje anular con radio exterior ro y área\(A_0\) se encuentra como
\[A_0 = \pi (r_o^2 - r_i^2) \to r_i = \sqrt{r_o^2 - (A_0/\pi)}\nonumber\]
Evaluando estas ecuaciones usando el mismo par y con\(r_o = 30\) mm, encontramos\(r_i = 28.2\) mm (un grosor de pared de 1.8 mm) y una tensión de\(\tau_{\theta z} = 44.5\) MPa. Esto es una reducción de 82% en el estrés. El valor de\(r\) en la fórmula de esfuerzo cortante elástico subió cuando fuimos al eje anular en lugar de sólido, pero esto fue más que compensado por el aumento en el momento de inercia\(J\), que varía a medida que\(r^4\).
Ejemplo\(\PageIndex{5}\)
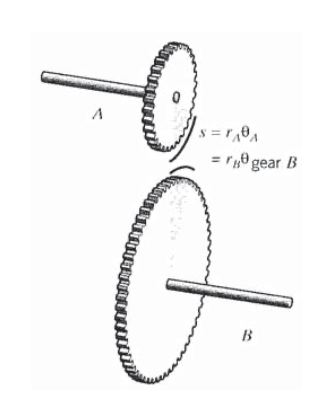
Al igual que con las cerchas, los desplazamientos angulares en los sistemas de barras de torsión se pueden encontrar a partir de consideraciones geométricas directas. En el caso del sistema de engranajes de dos varillas descrito anteriormente, el ángulo de torsión de la varilla\(A\) es
\[\theta_A = (\dfrac{L}{GJ})_A T_A = (\dfrac{L}{GJ})_A T \cdot \dfrac{r_A}{r_B}\nonumber\]
Esta rotación también será experimentada por el engranaje\(A\), por lo que un punto en su periferia barrerá a través de un arco\(S\) de
\[S = \theta_A r_A = (\dfrac{L}{GJ})_A T \cdot \dfrac{r_A}{r_B} \cdot r_A \nonumber\]
Dado que los engranajes\(A\) y\(B\) están conectados en sus periferias, el engranaje\(B\) girará a través de un ángulo de
\[\theta_{gear} B = \dfrac{S}{r_B} = (\dfrac{L}{GJ})_A \cdot \dfrac{r_A}{r_B} \cdot \dfrac{r_A}{r_B}\nonumber\]
(Ver Figura 11). Finalmente, el desplazamiento angular total en el extremo de la varilla\(B\) es la rotación del engranaje\(B\) más el giro de la varilla\(B\) misma:
\[\theta = \theta_{gear B} + \theta_{rod B} = (\dfrac{L}{GJ})_A T (\dfrac{r_A}{r_B})^2 + (\dfrac{L}{GJ})_B T\nonumber\]
Método de energía para desplazamiento rotacional
La deformación angular también se puede encontrar usando el Teorema de Castigliano (el Teorema de Castigliano se introduce en el Módulo 5, Trusses.), y en algunos problemas este enfoque puede ser más fácil. La energía de deformación por unidad de volumen en un material sometido a tensiones de cizallamiento elásticas\(\tau\) y deformaciones\(\gamma\) derivadas de torsión simple es:
\[U^* = \int \tau d\gamma = \dfrac{1}{2} \tau \gamma = \dfrac{\tau^2}{2G} = \dfrac{1}{2G} (\dfrac{Tr}{J})^2\nonumber\]
Esto se integra luego sobre el volumen de la muestra para obtener la energía total:
\[U = \int_V U^* dV = \int_L \int_A = \int_{L} \int_A \dfrac{1}{2G} (\dfrac{Tr}{J})^2 dA dz = \int_L \dfrac{T^2}{2GJ^2} \int_A r^2 dA\nonumber\]
\[U = \int_L \dfrac{T^2}{2GJ} dz\]
Si\(T, G, and J\) son constantes a lo largo de la longitud\(z\), esto se convierte simplemente
\[U = \dfrac{T^2L}{2GJ}\]
que es análogo a la expresión\(U = P^2L/2AE\) para especímenes de tracción.
En torsión, el ángulo\(\theta\) es el desplazamiento generalizado congruente con el momento aplicado\(T\), por lo que el teorema de Castigliano se aplica para una sola varilla de torsión como
\[\theta = \dfrac{\partial U}{\partial T} = \dfrac{TL}{GJ}\nonumber\]
como antes.
Ejemplo\(\PageIndex{6}\)
Considere los dos ejes engranados juntos discutidos anteriormente (Figura 11). El método de energía no requiere ningún razonamiento geométrico, y sigue inmediatamente una vez que se conocen los pares transmitidos por los dos ejes. Dado que los pares son constantes a lo largo de las longitudes, podemos escribir
\[U = \sum_i (\dfrac{T^2L}{2GJ})_i = (\dfrac{L}{2GJ})_A (T \dfrac{r_A}{r_B})^2 + (\dfrac{L}{2GJ})_B T^2\nonumber\]
\[\theta = \dfrac{\partial U}{\partial T} = (\dfrac{L}{GJ})_A (T \cdot \dfrac{r_A}{r_B}) (\dfrac{r_A}{r_B}) + (\dfrac{L}{GJ})_B T\nonumber\]
Secciones no circulares: la analogía de la membrana Prandtl
Los ejes con secciones no circulares no son infrecuentes. Aunque una forma circular es óptima desde una vista de análisis de tensiones, los ejes cuadrados o prismáticos pueden ser más fáciles de producir. Además, los ejes redondos a menudo tienen chaveteros u otras características geométricas necesarias para unirlos a los engranajes. Todo ello hace necesario poder hacer frente a secciones no circulares. Vamos a esbozar aquí una manera de hacer esto, en parte por su utilidad inherente y en parte para introducir un tipo de análisis experimental de estrés. Posteriormente, los módulos ampliarán estos métodos, y presentarán un tratamiento más completo de la teoría matemática subyacente.
La falta de simetría axial en secciones no circulares invalida el enfoque directo que condujo a la Ecuación 2.3.14, y un tratamiento minucioso debe atacar matemáticamente las ecuaciones diferenciales gobernantes del problema. Estas ecuaciones serán discutidas en módulos posteriores, pero basta con decir que pueden ser difíciles de resolver en forma cerrada para secciones transversales de forma arbitraria. El advenimiento de elementos finitos y otros métodos informáticos para resolver numéricamente estas ecuaciones ha eliminado esta dificultad hasta cierto punto, pero una limitación importante de las soluciones numéricas es que generalmente no logran proporcionar una visión intuitiva de por qué las distribuciones de estrés son como son: fallan en proporcionan pistas sobre cómo las tensiones podrían ser modificadas favorablemente por los cambios de diseño, y esta intuición es una de las herramientas más importantes del diseñador.
En una visión elegante, Prandtl (Ludwig Prandtl (1875—1953) es mejor conocido por su trabajo pionero en aerodinámica.) señaló que la distribución de esfuerzos en torsión puede describirse mediante una ecuación diferencial de “Poisson”, idéntica en forma a la que describe la deflexión de una membrana flexible soportada y presurizada desde abajo (J.P. Den Hartog, Advanced Strength of Materials, McGraw-Hill, Nueva York, 1952). Esto proporciona la base de la analogía de membrana Prandtl, que se utilizó durante muchos años para proporcionar una forma de análisis experimental de esfuerzos para ejes no circulares en torsión. Aunque este uso experimental ha sido suplantado por los métodos informáticos más convenientes, la analogía proporciona una visualización de tensiones inducidas por torsión que pueden proporcionar el tipo de conocimiento del diseño que buscamos.
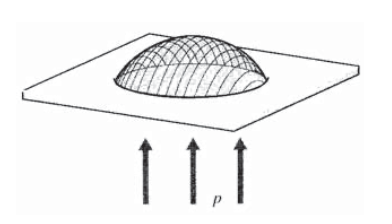
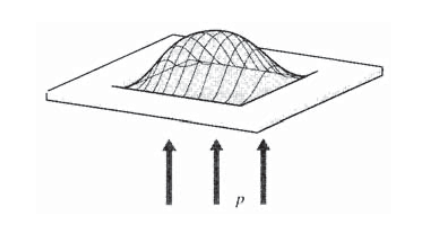
La analogía funciona de tal manera que las tensiones cortantes en un eje cargado torsionalmente de sección transversal arbitraria son proporcionales a la pendiente de una membrana flexible adecuadamente inflada. La membrana se sujeta de manera que sus bordes sigan una forma similar a la de la sección no circular, para luego desplazarse por la presión del aire. Visualice una lámina horizontal de metal con un orificio circular en ella, una lámina de caucho colocada debajo del orificio, y la goma ahora hecha para abultarse hacia arriba por presión que actúa desde debajo de la placa (ver Figura 13). El bulto será más empinado en los bordes y horizontal en su centro; es decir, su pendiente será cero en el centro y mayor en los bordes, al igual que las tensiones en un eje circular retorcido.
No es difícil visualizar que si el agujero fuera cuadrado como en la Figura 14 en lugar de redondo, la membrana se vería obligada a quedar plana (tener pendiente cero) en las esquinas, y tendría las pendientes más pronunciadas en los puntos medios de los bordes exteriores. Esto es justo lo que hacen las tensiones. Una buena razón para no usar secciones cuadradas para varillas de torsión, entonces, es que las esquinas no llevan tensión y por lo tanto son material desperdiciado. El diseñador podría eliminarlos sin consecuencias, siendo la decisión simplemente si el costo de hacer ejes circulares en lugar de cuadrados es más o menor que el costo del material desperdiciado. Para generalizar la lección en análisis de estrés, un ángulo sobresaliente no es peligroso en términos de estrés, solo derroche de material.
Pero a la inversa, un ángulo de entrada puede ser extremadamente peligroso. Una muesca afilada cortada en el eje es como un filo de cuchillo que corta en la membrana de goma, lo que hace que la goma esté casi vertical. Tales muescas o chaveteros son notorios elevadores de tensión, que muy a menudo actúan como los sitios de origen de las grietas por fatiga. Pueden ser necesarias en algunos casos, pero el diseñador debe ser dolorosamente consciente de sus consecuencias.
Ejercicio\(\PageIndex{1}\)
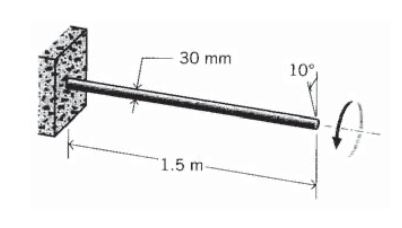
Una barra de torsión de 1.5 m de longitud y 30 mm de diámetro se sujeta en un extremo, y el extremo libre se tuerce en un ángulo de 10. Encuentre el esfuerzo cortante torsional máximo inducido en la barra.
Ejercicio\(\PageIndex{2}\)
La barra de torsión de Exercise\(\PageIndex{1}\) falla cuando el par aplicado es 1500 N-m. ¿Cuál es el módulo de ruptura en torsión? ¿Es esto lo mismo que el esfuerzo de cizallamiento máximo del material?
Ejercicio\(\PageIndex{3}\)
Un eje de transmisión de acero sólido debe ser capaz de transmitir 50 hp a 500 rpm. ¿Cuál debería ser su diámetro si el esfuerzo cortante torsional máximo se mantiene menos de la mitad del límite elástico a la tracción?
Ejercicio\(\PageIndex{4}\)
¿Cuánta potencia podría transmitir el eje de Prob. 3 (al mismo esfuerzo cortante torsional máximo) si se utilizara la misma cantidad de material en un eje anular en lugar de en un eje sólido? Tome el diámetro interior para que sea la mitad del diámetro exterior.
Ejercicio\(\PageIndex{5}\)
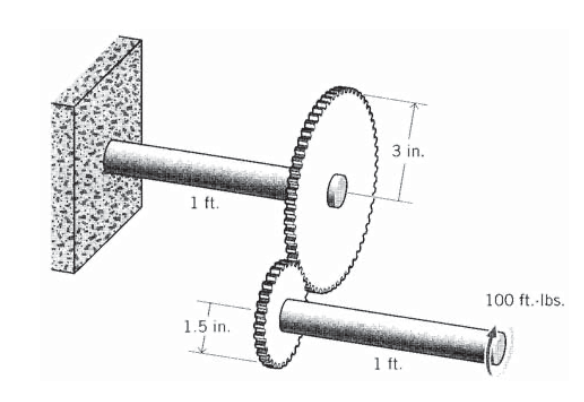
Dos ejes, cada uno de 1 pie de largo y 1 de diámetro, están conectados por un engranaje 2:1, y el extremo libre se carga con un par de 100 pies-lb. Encuentra el ángulo de giro en el extremo cargado.
Ejercicio\(\PageIndex{6}\)
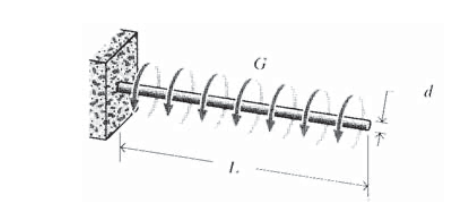
Un eje de longitud\(L\)\(d\), diámetro y módulo de cizallamiento\(G\) se carga con un momento de torsión uniformemente distribuido de\(T_0\) (N-m/m). (Por lo tanto, el\(T(x)\) momento\(x\) de torsión a una distancia del extremo libre es\(T_0x\).) Encuentra el ángulo de giro en el extremo libre.
Ejercicio\(\PageIndex{7}\)
Un eje compuesto de 3 pies de longitud se construye ensamblando una varilla de aluminio, de 2 de diámetro, sobre la cual se une un cilindro anular de acero de 0.5 en espesor de pared. Determine el esfuerzo cortante torsional máximo cuando el cilindro compuesto se somete a un par de 10,000 in-lb.
Ejercicio\(\PageIndex{8}\)
Dibuje la forma de una membrana inflada a través de una sección redonda que contiene una forma de chavetero entrante.


