3.1: Cinemática
- Page ID
- 83305
Introducción
Las ecuaciones cinemáticas o deformación-desplazamiento describen cómo las tensiones -el estiramiento y la distorsión- dentro de un cuerpo cargado se relacionan con los desplazamientos del cuerpo. Los componentes de desplazamiento en el\(x, y\), y las\(z\) direcciones se denotan por el vector\(u \equiv u_i \equiv (u,v,w)\), y son funciones de posición dentro del cuerpo:\(u = u(x, y, z)\). Si todos los puntos dentro del material experimentan el mismo desplazamiento (u = constante), la estructura se mueve como un cuerpo rígido, pero no se estira ni se deforma internamente. Para que se produzca el estiramiento, los puntos dentro del cuerpo deben experimentar diferentes desplazamientos.
Cepa infinitesimal
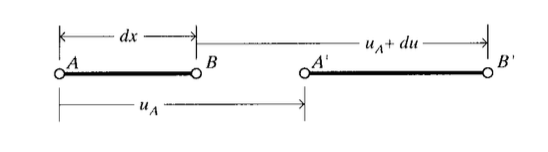
Considerar dos puntos\(A\) y\(B\) separados inicialmente por una pequeña distancia\(dx\) como se muestra en la Figura 1, y experimentar movimiento en la\(x\) dirección. Si el desplazamiento en el punto\(A\) es\(u_A\), el desplazamiento en\(B\) puede ser expresado por una expansión en serie de Taylor\(u(x)\) alrededor del punto\(x = A\):
\(u_B = u_A + du = u_A + \dfrac{\partial u}{\partial x} dx\)
donde aquí la expansión se ha truncado después del segundo término. El movimiento diferencial\(\delta\) entre los dos puntos es entonces
En nuestro concepto de estiramiento como el desplazamiento diferencial por unidad de longitud, el\(x\) componente de deformación es entonces
\[\epsilon_x = \dfrac{\delta}{dx} = \dfrac{\partial u}{\partial x}\]
De ahí que la deformación sea un gradiente de desplazamiento. Aplicando razonamiento similar al movimiento diferencial en la\(y\) dirección, el\(y\) -componente de deformación es el gradiente del desplazamiento vertical\(v\) con respecto a\(y\):
\[\epsilon_y = \dfrac{\partial v}{\partial y}\]
Figura 2: Distorsión por cizallamiento.
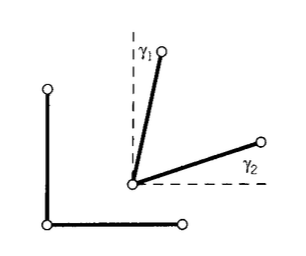
La distorsión del material, que puede describirse como el cambio en los ángulos originalmente rectos, es la suma de las inclinaciones impartidas a las líneas verticales y horizontales. Como se muestra en la Figura 2, la inclinación de una línea originalmente vertical es el desplazamiento horizontal relativo de dos puntos cercanos a lo largo de la línea:
El cambio de ángulo es entonces
\(\gamma_1 \approx \tan \gamma_1 = \dfrac{\delta}{dy} = \dfrac{\partial u}{\partial y}\)
De igual manera (ver Figura 3), la inclinación\(\gamma_2\) de una línea originalmente horizontal es el gradiente de\(v\) con respecto a\(x\). La deformación por cizallamiento en el\(xy\) plano es entonces
\[\gamma_{xy} = \gamma_1 + \gamma_2 = \dfrac{\partial v}{\partial x} + \dfrac{\partial u}{\partial y}\]
Esta notación, que se utiliza\(\epsilon\) para la deformación normal y\(\gamma\) para la deformación por cizallamiento, a veces se conoce como la descripción “clásica” de la deformación.
Formulación Matriz
La “notación indicial” descrita en el Módulo sobre Notación Matriz e Índice proporciona un método conciso para escribir todos los componentes de los estados tridimensionales de deformación:
\[\epsilon_{ij} = \dfrac{1}{2} \left ( \dfrac{\partial u_i}{\partial x_j} + \dfrac{\partial u_j}{\partial x_i} \right ) = \dfrac{1}{2} (u_{i,j} + u_{j, i})\]
donde la coma denota diferenciación con respecto a la siguiente variable espacial. Esta notación de índice de doble subíndice conduce naturalmente a una disposición matricial de los componentes de deformación, en la que el\(i-j\) componente de la deformación se convierte en el elemento de matriz en la\(i^{th}\) fila y la\(j^{th}\) columna:
\[\epsilon_{ij} = \begin{bmatrix} \tfrac{\partial u}{\partial x} & \tfrac{1}{2} (\tfrac{\partial u}{\partial y} + \tfrac{\partial v}{\partial x}) & \tfrac{1}{2} (\tfrac{\partial u}{\partial z}+ \tfrac{\partial w}{\partial x}) \\ \tfrac{1}{2} (\tfrac{\partial u}{\partial y} + \tfrac{\partial v}{\partial x}) & \tfrac{\partial v}{\partial y} & \tfrac{1}{2} (\tfrac{\partial v}{\partial z} + \tfrac{\partial w}{\partial y}) \\ \tfrac{1}{2} (\tfrac{\partial w}{\partial x} + \tfrac{\partial u}{\partial z}) & \tfrac{1}{2} (\tfrac{\partial v}{\partial z} + \tfrac{\partial w}{\partial y}) & \tfrac{\partial w}{\partial z} \end{bmatrix}\]
Obsérvese que la matriz de deformación es simétrica, es decir\(\epsilon_{ij} = \epsilon_{ji}\). Esta simetría significa que hay seis cepas independientes en lugar de nueve, como podría esperarse en una matriz\(\times\) 3 3. También tenga en cuenta que la descripción indicial de la cepa produce el mismo resultado para los componentes normales que en la descripción clásica:\(\epsilon_{11} = \epsilon_x\). Sin embargo, los componentes indiciales de la deformación por cizallamiento son la mitad de sus homólogos clásicos:\(\epsilon_{12} = \gamma_{xy}/2\).
En otro esquema notacional útil, las ecuaciones clásicas de deformación-desplazamiento se pueden escribir en una lista vertical, similar a un vector:
\(\left \{ \begin{array} {c} \epsilon_x \\ \epsilon_y \\ \epsilon_z \\ \gamma_{yz} \\ \gamma_{xz} \\ \gamma_{xy} \end{array} \right \} = \left \{ \begin{array} {c} {\partial u/\partial x} \\ {\partial v/\partial y} \\ {\partial w/\partial z} \\ {\partial v/\partial z + \partial w/\partial y} \\ {\partial u/\partial z + \partial w/\partial x} \\ {\partial u/\partial y + \partial v/\partial x} \end{array} \right \}\)
Esta disposición similar a un vector de los componentes de la cepa es solo por conveniencia, y a veces se llama pseudovector. La deformación es en realidad un tensor de segundo rango, como el estrés o el momento de inercia, y tiene propiedades matemáticas muy diferentes a las de los vectores. El orden de los elementos en forma pseudovector es arbitrario, pero es convencional enumerarlos como tenemos aquí moviendo hacia abajo la diagonal de la matriz de deformación de la Ecuación 5 de arriba izquierda a inferior derecha, luego subir la tercera columna, y finalmente mover una columna a la izquierda en la primera fila; esto da el ordenando 1,1; 2,2; 3,3; 2,3; 1,3; 1,2.
Siguiendo las reglas de multiplicación matricial, el pseudovector de cepa también se puede escribir en términos del vector de desplazamiento como
\[\left \{ \begin{array} {c} \epsilon_x \\ \epsilon_y \\ \epsilon_z \\ \gamma_{yz} \\ \gamma_{xz} \\ \gamma_{xy} \end{array} \right \} = \begin{bmatrix} \partial/\partial x & 0 & 0 \\ 0 & \partial/\partial y & 0 \\ 0 & 0 & \partial/\partial z \\ 0 & \partial /\partial z & \partial /\partial y \\ \partial /\partial z & 0 & \partial/\partial x \\ \partial/\partial y & \partial/\partial x & 0 \end{bmatrix} \left \{ \begin{array} {c} u \\ v \\ w \end{array} \right \}\]
La matriz entre paréntesis anteriores, cuyos elementos son operadores diferenciales, se puede abreviar como\(L\):
\[L = \begin{bmatrix} \partial/\partial x & 0 & 0 \\ 0 & \partial/\partial y & 0 \\ 0 & 0 & \partial/\partial z \\ 0 & \partial /\partial z & \partial /\partial y \\ \partial /\partial z & 0 & \partial/\partial x \\ \partial/\partial y & \partial/\partial x & 0 \end{bmatrix}\]
Las ecuaciones de deformación-desplazamiento se pueden escribir en forma concisa de “pseudovector-matriz”:
\[\epsilon = Lu\]
Ecuaciones como esta deben usarse en un contexto bien definido, ya que solo se aplican cuando se usa el listado de pseudovectores algo arbitrario de los componentes de la cepa.
Deformación volumétrica
Dado que la deformación normal es solo el cambio de longitud por unidad de longitud original, la nueva longitud\(L'\) después de la deformación se encuentra como
\[\epsilon = \dfrac{L' - L_0}{L_0} \Rightarrow L' = (1 + \epsilon) L_0\]
Si un elemento de volumen cúbico, originalmente de dimensión\(abc\), se somete a deformaciones normales en las tres direcciones, el cambio en el volumen del elemento es
\[\begin{array} {rcl} {\dfrac{\Delta V}{V}} & = & {\dfrac{a'b'c' - abc}{abc} = \dfrac{a(1 + \epsilon_x) b(1 + \epsilon_y) c(1+\epsilon_z) - abc}{abc}} \\ {} & = & {(1 + \epsilon_x)(1 + \epsilon_y)(1 +\epsilon_z) - 1 \approx \epsilon_x + \epsilon_y + \epsilon_z} \end{array}\]
donde se descuidan los productos de cepas en comparación con los valores individuales. La deformación volumétrica es por lo tanto la suma de las cepas normales, es decir, la suma de los elementos diagonales en la matriz de deformación (esto también se llama la traza de la matriz, o\(Tr[\epsilon]\)). En notación de índice, esto se puede escribir simplemente
\(\dfrac{\Delta V}{V} = \epsilon_{kk}\)
Esto se conoce como el componente volumétrico, o “dilatacional” de la deformación.
Ejemplo\(\PageIndex{1}\)
Para ilustrar cómo se calcula la deformación volumétrica, considere una lámina delgada de acero sometida a deformaciones en su plano dadas por\(\epsilon_x = 3, \epsilon_y = -4\), y\(\gamma_{xy} = 6\) (todas en\(\mu\) in/in). La lámina no está en deformación plana, ya que puede sufrir una deformación de Poisson en la\(z\) dirección dada por\(\epsilon_z = -\nu (\epsilon_x + \epsilon_y) = -0.3(3 - 4) = 0.3\). Por lo tanto, el estado total de deformación se puede escribir como la matriz
donde los corchetes en el\([\epsilon]\) símbolo enfatizan que se está utilizando la matriz en lugar de la forma pseudovector de la cepa. La deformación volumétrica es:
Los ingenieros a menudo se refieren a “micropulgadas” de tensión; realmente significan micropulgadas por pulgada. En el caso de la deformación volumétrica, la unidad correspondiente (pero incómoda) sería de micropulgadas cúbicas por pulgada cúbica.
Deformación finita
Las relaciones infinitesimales deformación-desplazamiento dadas por las Eqns. 3.1.1—3.1.3 se utilizan en la gran mayoría de los análisis mecánicos, pero no describen el estiramiento con precisión cuando los gradientes de desplazamiento se vuelven grandes. Esto ocurre a menudo cuando se están considerando polímeros (especialmente elastómeros). También se producen grandes deformaciones durante las operaciones de procesamiento de deformación, como el estampado de paneles de carrocería automotriz de acero. La cinemática de gran desplazamiento o deformación puede ser complicada y sutil, pero en la siguiente sección se esbozará una descripción simple de la deformación finita lagrangiana para ilustrar algunos de los conceptos involucrados.
Consideremos dos líneas ortogonales\(OB\) y\(O\) A como se muestra en la Figura 4, originalmente de longitud dx y dy, a lo largo de los\(x-y\) ejes, donde por conveniencia establecemos\(dx = dy = 1\). Después de la deformación, los extremos de estas líneas se mueven a nuevas posiciones\(A_1O_1B_1\) como se muestra. Describiremos estas nuevas posiciones usando el esquema de coordenadas de los\(x-y\) ejes originales, aunque también podríamos permitir que las nuevas posiciones definan un nuevo conjunto de ejes. Al seguir el movimiento de las líneas con respecto a las posiciones originales, estamos utilizando el llamado punto de vista lagrangiano. Podríamos haber usado alternativamente las posiciones finales como nuestra referencia; esta es la visión euleriana que se usa a menudo en mecánica de fluidos.
Después de esforzarse, la distancia\(dx\) se vuelve
\((dx)' = (1 + \dfrac{\partial u}{\partial x} dx\)
Usando nuestro pensamiento “pequeño” anterior, la tensión\(x\) -direction sería justa\(\partial u /\partial x\). Pero cuando las tensiones se hacen más grandes, también debemos considerar que el movimiento ascendente del punto\(B_1\) relativo a\(O_1\), es decir\(\partial v /\partial x\), también ayuda a estirar la línea\(OB\). Considerando ambos efectos, el teorema de Pitágoras da la nueva longitud\(O_1B_1\) como
\(O_1 B_1 = \sqrt{(1 + \dfrac{\partial u}{\partial x})^2 + (\dfrac{\partial v}{\partial x})^2}\)
Ahora definimos nuestra cepa Lagrangiana como

\ [4pt] &=\ sqrt {1 + 2\ dfrac {\ u parcial} {\ parcial x} +\ izquierda (\ dfrac {\ parcial u} {\ parcial x}\ derecha) ^2 +\ izquierda (\ dfrac {\ parcial v} {\ parcial x}\ derecha) ^2} - 1\ end {align*}\] </p lt-eng-445">
Usando la expansión de la serie\(\sqrt{1 + x} \approx 1 + x/2 + x^2/8 + \cdots\) y descuidando términos más allá del primer orden, esto se convierte
Del mismo modo, podemos mostrar
\[\epsilon_y = \dfrac{\partial v}{\partial y} + \dfrac{1}{2} \left [\left ( \dfrac{\partial v}{\partial y} \right )^2 \left ( \dfrac{\partial u}{\partial y} \right )^2 \right ]\]
\[\gamma_{xy} = \dfrac{\partial u}{\partial y} + \dfrac{\partial v}{\partial x} + \dfrac{\partial u}{\partial y} \dfrac{\partial u}{\partial x} + \dfrac{\partial v}{\partial y} \dfrac{\partial v}{\partial x}\]
Cuando las cepas son lo suficientemente pequeñas como para que los términos cuadráticos sean despreciables en comparación con los lineales, estos se reducen a las expresiones infinitesimal-strain mostradas anteriormente.
Ejemplo\(\PageIndex{2}\)
La función de desplazamiento\(u(x)\) para una muestra de tracción de sección transversal y longitud uniforme\(L\), fijada en un extremo y sometida a un desplazamiento\(\delta\) en el otro, es solo la relación lineal
\(u(x) = \left ( \dfrac{x}{L} \right ) \delta\)
La cepa Lagrangiana viene dada por la Ecuación 3.1.11 como
\(\epsilon_x = \dfrac{\delta}{L} + \dfrac{1}{2} \left ( \dfrac{\delta}{L} \right )^2\)
El primer término es la expresión familiar de cepas pequeñas, con el segundo término no lineal cada vez más importante a medida que\(\delta\) se hace más grande. Cuando\(\delta = L\), es decir, la cepa convencional es del 100%, existe una diferencia del 50% entre las medidas de deformación convencional y lagrangiana.
Los componentes de la cepa Lagrangiana pueden generalizarse usando notación de índice como
\(\epsilon_{ij} = \dfrac{1}{2} (u_{i,j} + u_{j, i} + u_{r, i} u_{r, j})\).
Una forma pseudovector también es conveniente ocasionalmente:
\[ \begin{align*} \left \{ \begin{array} {c} {\epsilon_x} \\ {\epsilon_y} \\ {\gamma_{xy}} \end{array} \right \} &= \left \{ \begin{array} {c} {u_{,x}} \\ {v_{,y}} \\ {u_{,y} + v_{,x}} \end{array} \right \} + \dfrac{1}{2} \begin{bmatrix} u_{,x} & v_{,x} & 0 & 0 \\ 0 & 0 & u_{,y} & v_{,y} \\ u_{,y} & v_{,y} & u_{,x} & v_{,x} \end{bmatrix} \left \{ \begin{array} {c} {u_{,x}} \\ {v_{,x}} \\ {u_{,y}} \\ {v_{,y}} \end{array} \right \} \\[4pt] &= \left (\begin{bmatrix} \partial /\partial x & 0 \\ 0 & \partial /\partial y \\ \partial /\partial y & \partial /\partial x \end{bmatrix} + \dfrac{1}{2} \begin{bmatrix} u_{,x} & v_{,x} & 0 & 0 \\ 0 & 0 & u_{,y} & v_{,y} \\ u_{,y} & v_{,y} & u_{,x} & v_{,x} \end{bmatrix} \begin{bmatrix} \partial /\partial x & 0 \\ 0 & \partial /\partial x \\ \partial /\partial y & 0 \\ 0 & \partial /\partial y \end{bmatrix}\right ) \left \{ \begin{array} {c} {u} \\ {v} \end{array} \right \} \end{align*}\]
que se puede abreviar
\[\epsilon = [L + A(u)]u\]
La matriz\(A(u)\) contiene el efecto no lineal de la cepa grande, y se vuelve insignificante cuando las cepas son pequeñas.
Ejercicio\(\PageIndex{1}\)
Escriba la ecuación abreviada de deformación-desplazamiento\(\epsilon = Lu\) (Ecuación 3.1.8) para dos dimensiones.
Ejercicio\(\PageIndex{2}\)
Escriba los componentes del tensor de tensión Lagrangiano en tres dimensiones:
\(\epsilon_{ij} = \dfrac{1}{2} (u_{i,j} + u_{j, i} + u_{r, i} u_{r, j})\)
Ejercicio\(\PageIndex{3}\)
Mostrar que para cepas pequeñas el cambio de volumen fraccional es la traza del tensor de tensión infinitesimal:
\(\dfrac{Delta V}{V} \equiv \epsilon_{kk} = \epsilon_x + \epsilon_y + \epsilon_z\)
Ejercicio\(\PageIndex{4}\)
Cuando el material es incompresible, mostrar que las relaciones de extensión están relacionadas por
\(\lambda_x \lambda_y \lambda_z = 1\)
Ejercicio\(\PageIndex{5}\)
Mostrar que las relaciones cinemáticas (deformación-desplazamiento) en las coordenadas polares se pueden escribir
\(\epsilon_r = \dfrac{\partial u_r}{\partial r}\)
\(\epsilon_{\theta} = \dfrac{1}{r} \dfrac{\partial u_{\theta}}{\partial \theta} +\dfrac{u_r}{r}\)


