3.2: Equilibrio
- Page ID
- 83311
Introducción
Las relaciones cinemáticas descritas en el Módulo 8 son puramente geométricas, y no implican consideraciones de comportamiento material. Las relaciones de equilibrio que se discutirán en este módulo tienen esta misma independencia del material. Simplemente son la ley del movimiento de Newton, afirmando que en ausencia de aceleración todas las fuerzas que actúan sobre un cuerpo (o una pieza de él) deben equilibrarse. Esto nos permite afirmar cómo el estrés dentro de un cuerpo, pero evaluado justo debajo de la superficie, se relaciona con la fuerza externa aplicada a la superficie. También gobierna cómo varía el estrés de una posición a otra dentro del cuerpo.
Estrés de Cauchy

En módulos anteriores, expresamos el esfuerzo normal como fuerza por unidad de área que actúa perpendicularmente a un área seleccionada, y un esfuerzo cortante fue una fuerza por unidad de área que actúa transversalmente al área. Para generalizar este concepto, considere la situación representada en la Figura 1, en la que un vector de tracción T actúa sobre un plano arbitrario dentro o sobre el límite externo del cuerpo, y en una dirección arbitraria con respecto a la orientación del plano. La tracción es un vector de fuerza simple que tiene magnitud y dirección, pero su magnitud se expresa en términos de fuerza por unidad de área:
\[T = \lim_{\Delta A \to 0} \left (\dfrac{\Delta F}{\Delta A} \right )\]
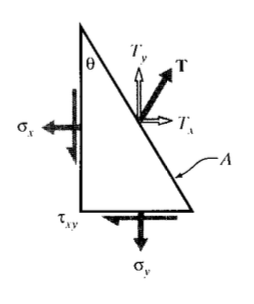
donde\(\Delta A\) es la magnitud del área sobre la que actúa ∆F. El Cauchy (Barón Augustin-Louis Cauchy (1789 {1857) fue un prolífico ingeniero y matemático francés) destaca, que son una generalización de nuestras definiciones anteriores de estrés, son las fuerzas por unidad de área que actúan sobre el cartesiano\(x\),\(y\), y\(z\) aviones para equilibrar la tracción. En dos dimensiones este balance se puede escribir dibujando un diagrama simple de cuerpo libre con el vector de tracción actuando sobre un área de tamaño arbitrario\(A\) (Figura 2), recordando obtener las fuerzas multiplicando por el área apropiada.
\(\sigma_x (A \cos \theta) + \tau_{xy} (A \sin \theta) = T_x A\)
\(\tau_{xy} (A \cos \theta) + \sigma_{y} (A \sin \theta) = T_y A\)
Cancelando el factor\(A\), esto se puede escribir en forma de matriz como
\[\begin{bmatrix} \sigma_x & \tau_{xy} \\ \tau_{xy} & \sigma_y \end{bmatrix} \left \{ \begin{array} {c} {\cos \theta} \\ {\sin \theta} \end{array} \right \} = \left \{ \begin{array} {c} {T_x} \\ {T_y} \end{array} \right \}\]
Ejemplo\(\PageIndex{1}\)
Considera una cavidad circular que contenga una presión interna\(p\). Los componentes del vector de tracción son entonces\(T_x = -p \cos \theta\),\(T_y = -p \sin \theta\). El cauchy cartesiano enfatiza en el material en el límite debe entonces satisfacer las relaciones
\(\sigma_x \cos \theta + \tau_{xy} \sin \theta = -p \cos \theta\)
\(\tau_{xy} \cos \theta + \sigma_y \sin \theta = -p \sin \theta\)
A\(\theta = 0, \sigma_x = -p, \sigma_y = \tau_{xy} = 0\); a\(\theta = \pi /2, \sigma_y = -p, \sigma_x = \tau_{xy} = 0\). El esfuerzo cortante\(\tau_{xy}\) desaparece para\(\theta = 0\) o\(\pi /2\); en el Módulo 10 se verá que las tensiones normales\(\sigma_x\) y por lo tanto\(\sigma_y\) son tensiones principales en esos puntos.

El vector\((\cos \theta, \sin \theta)\) del lado izquierdo de la Ecuación 3.2.2 es también el vector\(\hat{n}\) de cosenos de dirección de la normal al plano sobre el que actúa la tracción, y sirve para definir la orientación de este plano. Esta ecuación matricial, que a veces se llama relación de Cauchy, se puede abreviar como
\[[\sigma] \hat{n} = T\]
Los corchetes aquí sirven como un recordatorio de que el estrés se está escribiendo como la matriz cuadrada de la Ecuación 3.2.2 en lugar de en forma de pseudovector. Esta relación sirve para definir el concepto de tensión como una entidad que relaciona la tracción (un vector) que actúa sobre una superficie arbitraria con la orientación de la superficie (otro vector). Por lo tanto, el estrés es de mayor grado de abstracción que un vector, y técnicamente es un tensor de segundo rango. La diferencia entre vectores (tensores de primer rango) y tensores de segundo rango se manifiesta en cómo se transforman con respecto a las rotaciones de coordenadas, que se trata en el Módulo 10. Como se ilustra en el ejemplo anterior, la relación de Cauchy sirve tanto para definir el estrés como para calcular su magnitud en los límites donde se conocen las tracciones.

En tres dimensiones, la forma matricial del estado de tensión que se muestra en la Figura 4 es la matriz simétrica\(\times\) 3 3 obtenida por una extensión obvia de la de la Ecuación 3.2.2:
\[[\sigma] = \sigma_{i,j} = \begin{bmatrix} \sigma_x & \tau_{xy} & \tau_{xx} \\ \tau_{xy} & \sigma_y & \tau_{yx} \\ \tau_{xz} & \tau_{yz} & \sigma_z \end{bmatrix}\]
El elemento en la\(i^{\th}\) fila y la\(j^{th}\) columna de esta matriz es la tensión en la\(i^{th}\) cara en la\(j^{th}\) dirección. El equilibrio de momentos requiere que la matriz de esfuerzos sea simétrica, por lo que el orden de los subíndices de las tensiones de cizallamiento fuera de la diagonal es inmaterial.
Ecuaciones diferenciales de gobierno
Determinar la variación de los componentes de tensión como funciones de posición dentro del interior de un cuerpo es obviamente un objetivo principal en el análisis de estrés. Este es un tipo de problema de valor límite que a menudo se encuentra en la teoría de ecuaciones diferenciales, en las que se especifican los gradientes de las variables, en lugar de las propias variables explícitas. En el caso de la tensión, los gradientes se rigen por condiciones de equilibrio estático: las tensiones no pueden cambiar arbitrariamente entre dos puntos\(A\) y\(B\), o el material entre esos dos puntos puede no estar en equilibrio.

Para desarrollar esta idea formalmente, requerimos que el valor integrado de la tracción superficial T sobre la superficie\(A\) de un elemento de volumen arbitrario\(dV\) dentro del material (ver Figura 5) debe sumarse a cero para mantener el equilibrio estático:
\(0 = \int_A T dA = \int_A [\sigma] \hat{n} dA\)
Aquí asumimos la falta de fuerzas gravitacionales, centrípetas u otras fuerzas “corporales” que actúan sobre el material dentro del volumen. La integral de superficie en esta relación se puede convertir en una integral de volumen mediante el teorema de divergencia de Gauss (el teorema de Gauss establece que\(\int_A X \hat{n} dA = \int_S \nabla X dV\) donde\(X\) es una cantidad escalar, vector o tensor. ):
\(\int_V \nabla [\sigma] dV = 0\)
Dado que el volumen\(V\) es arbitrario, esto requiere que el integrando sea cero:
\[\nabla [\sigma] = 0\]
Para problemas cartesianos en tres dimensiones, esto se expande a:
\[\begin{array} {c} {\tfrac{\partial \sigma_x}{\partial x} + \tfrac{\partial \tau_{xy}}{\partial y} + \tfrac{\partial \tau_{xz}}{\partial z} = 0} \\ {\tfrac{\partial \tau_{xy}}{\partial x} + \tfrac{\partial \sigma_y}{\partial y} + \tfrac{\partial \tau_{yz}}{\partial z} = 0} \\ {\tfrac{\partial \tau_{xz}}{\partial x} + \tfrac{\partial \tau_{yz}}{\partial y} + \tfrac{\partial \sigma_z}{\partial x} = 0} \end{array}\]
Usando la notación de índice, estos pueden escribirse:
\[\sigma_{ij, j} = 0\]
O en forma pseudovector-matriz, podemos escribir
\[\begin{bmatrix} \tfrac{\partial}{\partial x} & 0 & 0 & 0 & \tfrac{\partial}{\partial z} & \tfrac{\partial}{\partial y} \\ 0 & \tfrac{\partial}{\partial y} & 0 & \tfrac{\partial}{\partial z} & 0 & \tfrac{\partial}{\partial x} \\ 0 & 0 & \tfrac{\partial}{\partial z} & \tfrac{\partial}{\partial y} & \tfrac{\partial}{\partial x} & 0 \end{bmatrix} \left \{ \begin{array} {c} {\sigma_x} \\ {\sigma_y} \\ {\sigma_z} \\ {\tau_{yz}} \\ {\tau_{xz}} \\ {\tau_{xy}} \end{array} \right \} = \left \{ \begin{array} {c} {0} \\ {0} \\ {0} \end{array} \right \}\]
Al señalar que la matriz de operador diferencial entre paréntesis es solo la transformada de la que apareció en la Ecuación 3.2.7 del Módulo 8, podemos escribir esto como:
\[L^T \sigma = 0\]
Ejemplo\(\PageIndex{2}\)
No es difícil llegar a funciones de estrés que satisfagan las ecuaciones de equilibrio; cualquier constante servirá, ya que los gradientes de tensión serán entonces idénticamente cero. El problema es que también deben satisfacer las condiciones de límite, y esto complica las cosas considerablemente. Posteriormente los módulos describirán varios enfoques para resolver las ecuaciones directamente, pero en algunos casos simples se puede ver una solución por inspección.

Considere una muestra de tracción sometida a una carga\(P\) como se muestra en la Figura 6. Una solución de prueba que sin duda satisface las ecuaciones de equilibrio es
\[[\sigma] = \begin{bmatrix} c & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} \nonumber\]
donde\(c\) es una constante debemos elegir para satisfacer las condiciones de contorno. Para mantener el equilibrio horizontal en el diagrama de cuerpo libre de la Figura 6 (b), es inmediatamente obvio que\(cA = P\), o\(\sigma_x = c = P/A\). Esta relación familiar se utilizó en el Módulo 1 para definir el estrés, pero vemos aquí que se puede ver como una consecuencia de consideraciones de equilibrio más que como una definición básica.
Ejercicio\(\PageIndex{1}\)
Determinar si el siguiente estado de estrés satisface el equilibrio:
\([\sigma] = \begin{bmatrix} 2x^3y^2 & -2x^2y^3 \\ -2x^2y^3 & xy^4 \end{bmatrix}\)
Ejercicio\(\PageIndex{2}\)
Desarrollar la forma bidimensional de las ecuaciones de equilibrio cartesiano dibujando un diagrama de cuerpo libre de una sección infinitesimal:

Ejercicio\(\PageIndex{3}\)
Usa el diagrama de cuerpo libre del problema anterior para mostrarlo\(\tau_{xy} = \tau_{yx}\).
Ejercicio\(\PageIndex{4}\)
Utilice un enfoque de diagrama de cuerpo libre para mostrar que en coordenadas polares las ecuaciones de equilibrio son
\(\dfrac{\partial \tau_{r \theta}}{\partial r} + \dfrac{1}{r} \dfrac{\partial \sigma_{\theta}}{\partial \theta} + 2 \dfrac{\tau_{r \theta}}{r} = 0\)
Ejercicio\(\PageIndex{5}\)
Desarrollar las ecuaciones anteriores para el equilibrio en coordenadas polares transformando las ecuaciones cartesianas usando
\(x = r \cos \theta\)
\(y = r \sin \theta\)
Ejercicio\(\PageIndex{6}\)
La función de estrés Airy\(\phi (x, y)\) se define de tal manera que las tensiones de Cauchy cartesianas son


