4.1: Diagramas de momento de corte y flexión
- Page ID
- 83296
Introducción
Las vigas son elementos estructurales largos y delgados, que difieren de los elementos de celosía en que están llamados a soportar cargas transversales y axiales. Sus puntos de fijación también pueden ser más complicados que los de los elementos de celosía: pueden estar atornillados o soldados entre sí, por lo que los accesorios pueden transmitir momentos de flexión o fuerzas transversales a la viga. Las vigas se encuentran entre los elementos estructurales más comunes, siendo los marcos de soporte de aviones, edificios, automóviles, personas y mucho más.
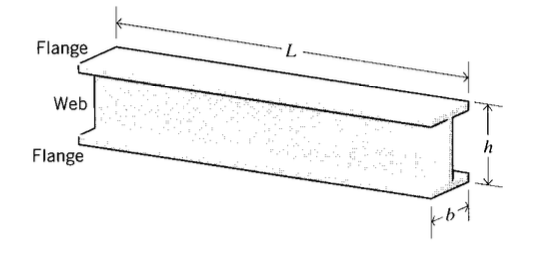
La nomenclatura de las vigas es bastante estándar: como se muestra en la Figura 1,\(L\) es la longitud, o lapso;\(b\) es la anchura, y\(h\) es la altura (también llamada profundidad). La forma de la sección transversal no necesita ser rectangular, y a menudo consiste en una banda vertical que separa fllanges horizontales en la parte superior e inferior de la viga (Hay un protocolo estandarizado para denotar vigas de acero estructural; por ejemplo W 8 × 40 indica una viga de amplio rango con una profundidad nominal de 8′′ y con un peso de 40 lb/ft de largo)
Como se verá en los Módulos 13 y 14, las tensiones y deflexiones inducidas en una viga bajo cargas de flexión varían a lo largo y altura de la viga. El primer paso para calcular estas cantidades y su variación espacial consiste en construir diagramas de cizallamiento y momento de flexión,\(V(x)\) y\(M(x)\), que son las fuerzas de corte internas y los momentos de flexión inducidos en la viga, trazados a lo largo de la longitud de la viga. En las siguientes secciones se describirá cómo se hacen estos diagramas.
Diagramas de cuerpo libre
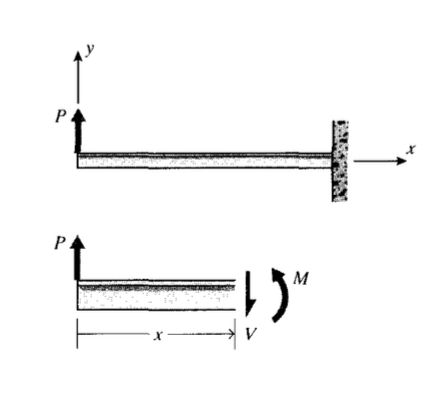
Como simple ejemplo inicial, considere una viga sujeta (\ cantileverada”) en un extremo y sometida a una carga\(P\) en el extremo libre como se muestra en la Figura 2. Un diagrama de cuerpo libre de una sección cortada transversalmente en posición\(x\) muestra que una fuerza de corte\(V\) y un momento\(M\) deben existir en la sección de corte para mantener el equilibrio. Mostraremos en el Módulo 13 que estos son los resultados de cizallamiento y tensiones normales que se establecen en planos internos por las cargas de flexión. Como de costumbre, consideraremos positivas las áreas de sección cuyas normales apuntan en la\(x\) dirección +; luego las fuerzas de cizallamiento que apuntan en la\(y\) dirección + sobre las\(x\) caras + se considerarán positivas. Los momentos cuya dirección vectorial dada por la regla de la derecha está en la\(z\) dirección + (vector fuera del plano del papel, o que tiende a causar rotación en sentido contrario a las agujas del reloj en el plano del papel) serán positivos al actuar sobre +\(x\) caras. Otra forma de reconocer los momentos de flexión positivos es que hacen que la forma de flexión sea cóncava hacia arriba. Para este ejemplo beam, las ecuaciones estáticas dan:
\[\sum F_y = 0 = V + P \Rightarrow V = \text{constant} = -P\]
\[\sum M_0 = 0 = -M + Px \Rightarrow M = M(x) = Px\]
Tenga en cuenta que el momento aumenta con la distancia desde el extremo cargado, por lo que la magnitud del valor máximo de\(M\) comparado con\(V\) aumenta a medida que la viga se alarga. Esto es cierto para la mayoría de las vigas, por lo que los efectos de cizallamiento suelen ser más importantes en vigas con pequeñas relaciones de longitud a altura.
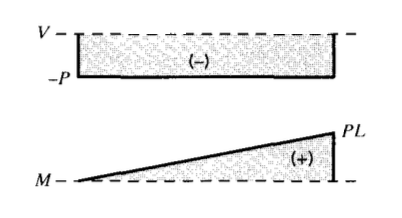
Como se indicó anteriormente, se demostrará que las tensiones y defflecciones son funciones de\(V\) y\(M\), por lo que es importante poder calcular cómo varían estas cantidades a lo largo de la longitud de la viga. Las parcelas de\(V(x)\) y\(M(x)\) se conocen como diagramas de cizallamiento y momento de flexión, y es necesario obtenerlas antes de que se puedan determinar las tensiones. Para el voladizo de carga final, los diagramas mostrados en la Figura 3 son obvios a partir de las ecuaciones 4.1.1 y 4.1.2.
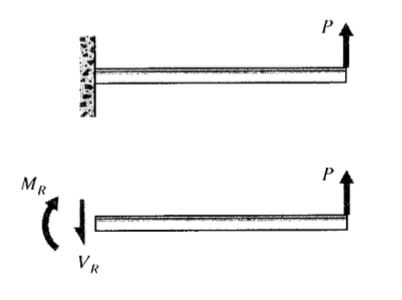
Fue más fácil analizar la viga en voladizo comenzando por el extremo libre, pero la elección de origen es arbitraria. No siempre es posible adivinar la forma más fácil de proceder, así que considera qué habría pasado si el origen se hubiera colocado en la pared como en la Figura 4. Ahora cuando se construye un diagrama de cuerpo libre, se deben colocar fuerzas en el origen para reemplazar las reacciones que fueron impuestas por la pared para mantener la viga en equilibrio con la carga aplicada. Estas reacciones se pueden determinar a partir de diagramas de cuerpo libre del haz como un todo (si el haz está determinado estáticamente), y deben ser encontradas antes de que el problema pueda continuar. Para la viga de la Figura 4:
\(\sum F_y = 0 = -V_R + P \Rightarrow V_R = P\)
El momento de cizallamiento y flexión en\(x\) son entonces
\(V(x) = V_R = P = \text{constant}\)
Esta elección de origen produce algo de álgebra extra, pero los\(M(x)\) diagramas\(V(x)\) y mostrados en la Figura 5 son los mismos que antes (a excepción de los cambios de signo):\(V\) es constante e igual a\(P\), y\(M\) varía linealmente de cero en el extremo libre a\(PL\) en la pared.
Cargas distribuidas
Las cargas transversales se pueden aplicar a las vigas de una manera distribuida en lugar de en un punto como se representa en la Figura 6, que podrían visualizarse como arena apilada sobre la viga. Es conveniente describir estas cargas distribuidas en términos de fuerza por unidad de longitud, de manera que esa\(q(x)\) sería la carga aplicada a una pequeña sección de longitud\(dx\) por una carga distribuida\(q(x)\). La fuerza cortante\(V(x)\) establecida en reacción a tal carga es
\[V(x) = - \int_{x_0}^{x} q(\xi) d \xi\]
Figura 5: Diagramas alternativos de cizallamiento y momento de flexión para la viga en voladizo.
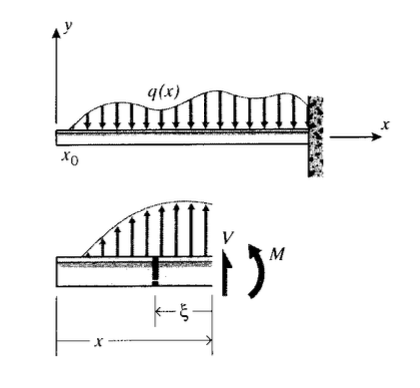
donde\(x_0\) es el valor de\(x\) en el que comienza\ q (x)\), y\(\xi\) es una variable de longitud ficticia que mira hacia atrás desde\(x\). De ahí\(V(x)\) está el área bajo el\(q(x)\) diagrama hasta la posición\(x\). El balance de momentos se obtiene considerando el incremento de carga\(q(\xi) d \xi\) aplicado a un pequeño ancho\(d \xi\) de viga, a una distancia\(\xi\) desde el punto\(x\). El momento incremental de esta carga alrededor del punto\(x\) es\(q(\xi) \xi d \xi\), entonces el momento\(M(x)\) es
\[M = \int_{x_0}^{x} q(\xi) \xi d \xi\]
Esto puede estar relacionado con el centroide del área bajo la\(q(x)\) curva hasta\(x\), cuya distancia desde\(x\) es
\(\bar{\xi} = \dfrac{\int q(\xi) \xi d \xi}{\int q (\xi) d\xi}\)
De ahí que la Ecuación 4.1.4 se pueda escribir
\[M = Q \bar{\xi}\]
donde\(Q = \int q (\xi) d\xi\) esta la zona. Por lo tanto, la carga distribuida\(q(x)\) es estáticamente equivalente a una carga concentrada de magnitud\(Q\) colocada en el centroide del área bajo el\(q(x)\) diagrama.
Ejemplo\(\PageIndex{1}\)
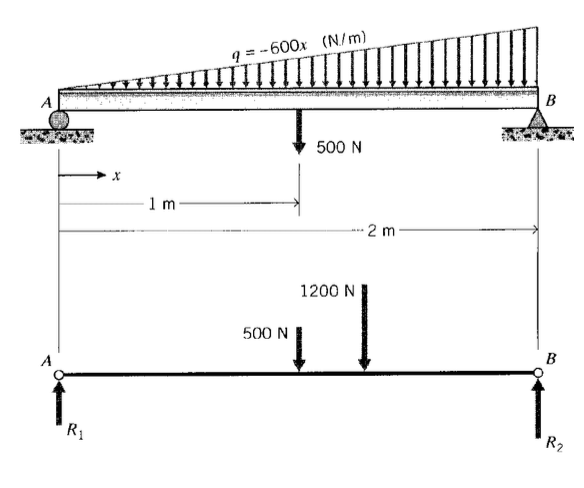
Considere una viga de soporte simple que lleve una carga triangular y una carga concentrada como se muestra en la Figura 7. Con el propósito de determinar las fuerzas de reacción de soporte\(R_1\) y\(R_2\), la carga triangular distribuida puede ser reemplazada por su equivalente estático. La magnitud de esta fuerza equivalente es
La fuerza equivalente actúa a través del centroide del área triangular, que es 2/3 de la distancia desde su extremo estrecho (ver Exercis\(\PageIndex{1}\)). La reacción ahora se\(R_2\) puede encontrar tomando momentos alrededor del extremo izquierdo:
La otra reacción se puede encontrar a partir del equilibrio vertical:
Método de integración sucesiva
Figura 8: Relaciones entre cargas distribuidas y fuerzas de corte internas y momentos de flexión.
Ya hemos observado en la Ecuación 4.1.3 que la curva de cizallamiento es la integral negativa de la curva de carga. Otra forma de desarrollar esto es considerar un equilibrio corporal libre en un pequeño incremento de longitud\(dx\) sobre el cual la cizalla y el momento cambian de\(V\) y\(M\) hacia\(V + dV\) y\(M + dM\) (ver Figura 8). La carga distribuida se\(q(x)\) puede tomar como constante en el intervalo pequeño, por lo que el equilibrio de fuerzas es:
\[\dfrac{dV}{dx} = -q\]
o
\[V(x) = - \int q(x) \ dx\]
que es equivalente a la Ecuación 4.1.3. Un momento de equilibrio alrededor del centro del incremento da
A medida que el incremento\(dx\) se reduce al límite, el término que contiene el diferencial de orden superior\(dV\ dx\) desaparece en comparación con los demás, dejando
\[\dfrac{dM}{dx} = -V\]
o
\[M(x) = -\int V(x)\ dx\]
De ahí que el valor de la curva de cizallamiento en cualquier ubicación axial a lo largo de la viga sea igual al negativo de la pendiente de la curva de momento en ese punto, y el valor de la curva de momento en cualquier punto es igual al negativo del área bajo la curva de cizallamiento hasta ese punto.
Las curvas de cizallamiento y momento se pueden obtener por integración sucesiva de la\(q(x)\) distribución, como se ilustra en el siguiente ejemplo.
Ejemplo\(\PageIndex{2}\)
Considere una viga en voladizo sometida a una carga distribuida negativa\(q(x) = -q_0\) = constante como se muestra en la Figura 9; luego
\(V(x) = -\int q(x)\ dx = q_0 x + c_1\)
donde\(c_1\) es una constante de integración. Un diagrama de cuerpo libre de una pequeña astija de longitud cercana\(x = 0\) muestra eso\(V(0) = 0\), por lo que también\(c_1\) debe ser cero. La función momento se obtiene integrando de nuevo:
\(M(x) = -\int V(x) \ dx = -\dfrac{1}{2} q_0 x^2 + c_2\)
donde\(c_2\) hay otra constante de integración que también es cero, ya que\(M(0) = 0\).
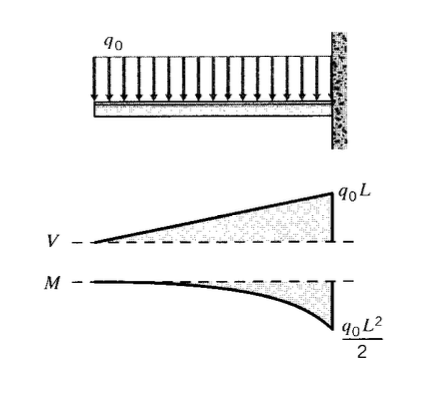
Es cierto que este problema fue fácil porque elegimos uno con condiciones de límite nulo, y con solo un segmento de carga. Cuando las cargas concentradas o distribuidas se encuentran en diferentes
posiciones a lo largo de la viga, es necesario integrar sobre cada sección entre cargas por separado. Cada integración producirá una constante desconocida, y éstas deberán determinarse invocando la continuidad de pendientes y defflecciones de sección a sección. Se trata de un proceso laborioso, pero que se puede hacer mucho más fácil utilizando funciones de singularidad que se introducirán en breve.
A menudo es posible bosquejar\(V\) y\(M\) diagramas sin realmente dibujar diagramas de cuerpo libre o escribir ecuaciones de equilibrio. Esto se hace más fácil porque las curvas son integrales o derivadas entre sí, por lo que el boceto gráfico puede aprovechar las relaciones entre pendientes y áreas.
Estas reglas se pueden utilizar para trabajar gradualmente de la\(q(x)\) curva a\(V(x)\) y luego a\(M(x)\). Dondequiera que aparezca una carga concentrada en la viga, la\(V(x)\) curva debe saltar en ese valor, pero en sentido contrario; de manera similar, la\(M(x)\) curva debe saltar discontinuamente dondequiera que se aplique una pareja a la viga.
Ejemplo\(\PageIndex{3}\)
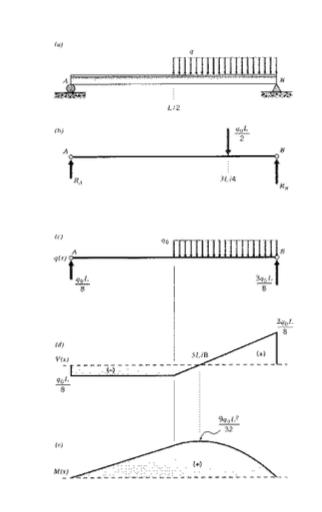
Para ilustrar este proceso, considere una viga de longitud simplemente soportada\(L\) como se muestra en la Figura 10, cargada a lo largo de la mitad de su longitud por una carga distribuida negativa\(q = -q_0\). La solución\(V(x)\) y\(M(x)\) toma los siguientes pasos:
1. Las reacciones en los soportes se encuentran a partir del equilibrio estático. Sustitución de la carga distribuida por una carga concentrada\(Q = -q_0 (L/2)\) en el punto medio de la\(q\) distribución (Figura 10 (b)) y tomando momentos alrededor\(A\):
\(R_B L = (\dfrac{q_0L}{2}) (\dfrac{3L}{4}) \Rightarrow R_B = \dfrac{3q_0L}{8}\)
La reacción en el extremo derecho se encuentra luego a partir de un equilibrio de fuerzas vertical:
Tenga en cuenta que solo se disponía de dos ecuaciones de equilibrio, ya que un balance de fuerzas horizontal no proporcionaría información relevante. De ahí que el haz sea estáticamente indeterminado si hay más de dos soportes presentes.
El\(q(x)\) diagrama es entonces solo el haz con las reacciones finales mostradas en la Figura 10 (c).
2. Comenzando el diagrama de corte a la izquierda,\(V\) inmediatamente salta hacia abajo a un valor de\(-q_0 L/8\) en oposición a la fuerza de reacción aplicada discontinuamente en\(A\); permanece en este valor hasta\(x = L/2\) como se muestra en la Figura 10 (d).
3. En\(x = L/2\), la\(V(x)\) curva comienza a elevarse con una pendiente constante de a\(+ q_0\) medida que el área bajo la\(q(x)\) distribución comienza a acumularse. Cuando\(x = L\), la curva de cizallamiento habrá aumentado en una cantidad\(q_0 L/2\), el área total bajo la\(q(x)\) curva; su valor es entonces\((-q_0 l/8) + (q_0 L/2) = (3q_0 L/8)\). La curva de cizallamiento luego cae a cero en oposición a la fuerza de reacción\(R_B = (3q_0 L/8)\). (Los\(M\) diagramas\(V\) y siempre deben cerrarse, y esto proporciona una verificación de la obra).
4. El diagrama de momento comienza desde cero como se muestra en la Figura 10 (e), ya que no hay momento aplicado discontinuamente en el extremo izquierdo. Se mueve hacia arriba a una pendiente constante de\(+q_0L/8\), el valor del diagrama de cizallamiento en la primera mitad de la viga. Cuando\(x = L/2\), habrá subido a un valor de\(q_0 L^2/16\).
5. Después\(x = L/2\), la pendiente del diagrama de momento comienza a caer a medida que aumenta el valor del diagrama de cizallamiento. El diagrama de momento es ahora parabólico, siendo siempre un orden más alto que el diagrama de corte. El diagrama de corte cruza el\(V = 0\) eje en\(x = 5L/8\), y en este punto la pendiente del diagrama de momento habrá caído a cero. El valor máximo de\(M\) es\(9q_0 L^2/32\), el área total bajo la\(V\) curva hasta este punto.
6. Después\(x = 5L/8\), el diagrama de momento cae parabólicamente, llegando a cero a\(x = L\).
Funciones de singularidad
Esta familia especial de funciones proporciona una forma automática de manejar las irregularidades de carga que suelen ocurrir en problemas de viga. Se parecen mucho a los factores polinomiales convencionales, pero con la propiedad de ser cero hasta que se “activan” en los puntos deseados a lo largo del haz. La definición formal es
\[f_n (x) = \langle x - a \rangle^n = \begin{cases} 0, & x < a \\ (x - a)^n, & x > a \end{cases}\]
donde\(n = -2, -1, 0, 1, 2, \cdots\). La función\(\langle x - a \rangle^0\) es una función de paso de unidad,\(\langle x - a \rangle_{-1}\) es una carga concentrada, y\(\langle x - a \rangle_{-2}\) es un par concentrado. Las cinco primeras de estas funciones se esbozan en la Figura 11.
Figura 11: Funciones de singularidad.
Las funciones de singularidad están integradas al igual que los polinomios convencionales:
\[\int_{-\infty}^{x} \langle x - a \rangle^n \ dx = \dfrac{\langle x - a \rangle^{n+1}}{n + 1} \ n \ge 0\]
Sin embargo, existen reglas especiales de integración para los\(n = -2\) miembros\(n = -1\) y, y este manejo especial se enfatiza mediante el uso de subíndices para el\(n\) índice:
\[\int_{\infty}^{x} \langle x - a \rangle_{-2}\ dx = \langle x - a \rangle_{-1}\]
\[\int_{\infty}^{x} \langle x - a \rangle_{-1}\ dx = \langle x - a \rangle^0\]
Ejemplo\(\PageIndex{4}\)
Aplicando funciones de singularidad al haz del Ejemplo 4.3, se escribiría la función de carga
También se podría incluir la fuerza de reacción en el extremo derecho, pero solo se activa cuando el problema termina. Integrando una vez:
Aquí se incluye automáticamente la constante de integración, ya que se\(A\) ha incluido explícitamente la influencia de la reacción at. Integrando de nuevo:
El examen de este resultado demostrará que es el mismo que el desarrollado anteriormente.
El software de manipulación\(^{\text{TM}}\) simbólica Maple proporciona un medio eficiente para trazar estas funciones. A continuación se muestra cómo se podría trazar la ecuación de momento de este ejemplo, utilizando la función Heaviside para proporcionar la singularidad.
# Define function sfn in terms of a and n
>sfn:=proc(a,n) (x-a)^n*Heaviside(x-a) end;
sfn := proc(a, n) (x - a)^n*Heaviside(x - a) end proc
# Input moment equation using singularity functions
>M(x):=(q*L/8)*sfn(0,1)-(q/2)*sfn(L/2,2);
M(x) := 1/8 q L x Heaviside(x) 2
-1/2q(x-1/2L) Heaviside(x-1/2L)
# Provide numerical values for q and L: >q:=1: L:=10:
# Plot function >plot(M(x),x=0..10);
Figura 12: Gráfica de singularidad de arce
Ejercicio\(\PageIndex{1}\)
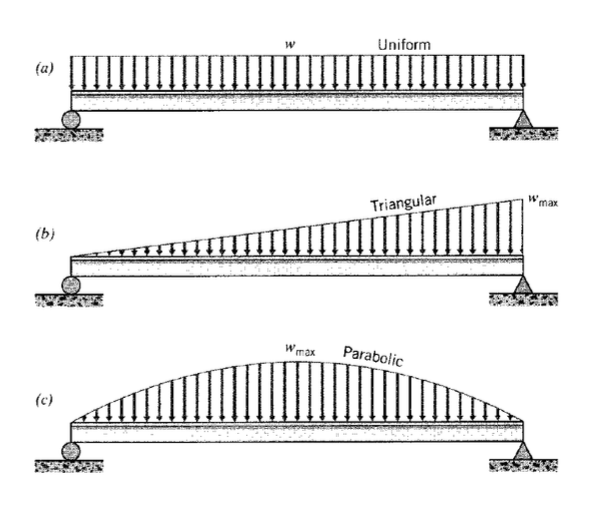
(a) - (c) Localizar la magnitud y posición de la fuerza equivalente a las distribuciones de carga aquí mostradas.
Ejercicio\(\PageIndex{2}\)
a) - c) Determinar las fuerzas de reacción en los apoyos de los casos en Ejercicio\(\PageIndex{1}\).
Ejercicio\(\PageIndex{3}\)
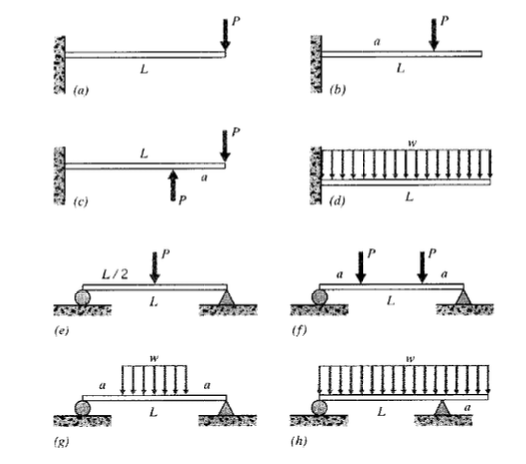
(a) - (h) Esboce los diagramas de cizallamiento y momento de flexión para los casos de carga que se muestran aquí.
Ejercicio\(\PageIndex{4}\)
(a) - (h) Escribir expresiones de función de singularidad para las distribuciones de cizallamiento y momento de flexión para los casos en Ejercicio\(\PageIndex{3}\).
Ejercicio\(\PageIndex{5}\)
(a) - (h) Utilice Maple (u otro) software para trazar las distribuciones de cizallamiento y momento de flexión para los casos en Ejercicio\(\PageIndex{3}\), utilizando los valores (según sea necesario)\(L = 25 \ in, a = 5\ in, w = 10\ lb/in, P = 150 \ lb\).
Ejercicio\(\PageIndex{6}\)
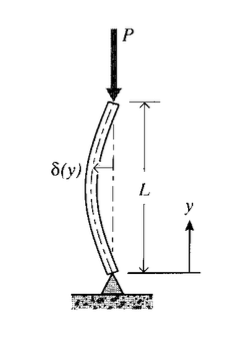
Los deflectos transversales\(n\) de una viga bajo una carga axial\(P\) se toman para ser\(\delta (y) = \delta_0 \sin (y \pi /L)\), como se muestra aquí. Determine el momento de flexión\(M(y)\) a lo largo de la viga.
Ejercicio\(\PageIndex{7}\)
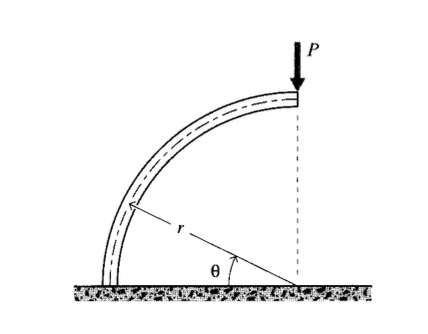
Determinar el momento de flexión\(M(\theta)\) a lo largo de la viga curva circular mostrada.