4.2: Tensiones en Vigas

Introducción

La comprensión de las tensiones inducidas en las vigas por las cargas de flexión tardó muchos años en desarrollarse. Galileo trabajó en este problema, pero la teoría tal como la usamos hoy en día suele atribuirse principalmente al gran matemático Leonard Euler (1707—1783). Como se desarrollará a continuación, las vigas desarrollan tensiones normales en la dirección longitudinal que varían desde un máximo en tensión en una superficie, a cero en el plano medio de la viga, hasta un máximo en compresión en la superficie opuesta. También se inducen esfuerzos cortantes, aunque a menudo son insignificantes en comparación con los esfuerzos normales cuando la relación longitud-altura de la viga es grande. Los procedimientos para calcular estas tensiones para diversas condiciones de carga y formas de sección transversal de viga son quizás los métodos más importantes que se encuentran en la introducción Mecánica de Materiales, y se desarrollarán en las secciones a seguir. Esta teoría requiere que el usuario sea capaz de construir diagramas de cizallamiento y momento de flexión para la viga, tal como se desarrolló por ejemplo en el Módulo 12.

Esfuerzos Normales

Una viga sometida a un momento de flexión positivo tenderá a desarrollar una curvatura cóncava-ascendente. Intuitivamente, esto significa que el material cerca de la parte superior de la viga se coloca en compresión a lo largo de la\(x\) dirección, con la región inferior en tensión. En la transición entre las regiones de compresión y tracción, la tensión se vuelve cero; este es el eje neutro de la viga. Si el material tiende a fallar en tensión, como tiza o vidrio, lo hará por iniciación de grietas y crecimiento desde la superficie de tracción inferior. Si el material es fuerte en tensión pero débil en compresión, fallará en la superficie compresiva superior; esto podría observarse en una pieza de madera por un pandeo compresivo de las fibras externas.

Buscamos una expresión que relacione las magnitudes de estas tensiones axiales normales con el momento de cizallamiento y flexión dentro de la viga, análogamente a las tensiones cortantes inducidas en un eje circular por torsión. De hecho, el desarrollo de las relaciones necesarias sigue exactamente el mismo enfoque directo que el utilizado para la torsión:

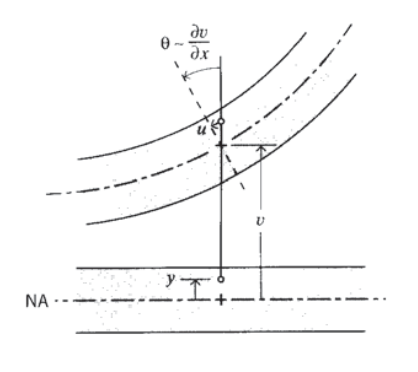
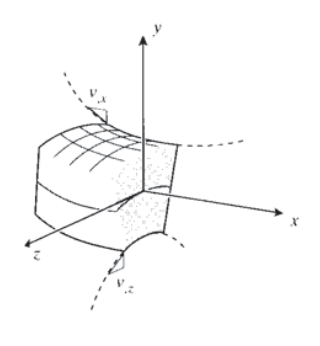
1. Declaración geométrica: Comenzamos por afirmar que los planos originalmente transversales dentro de la viga permanecen planos bajo flexión, pero giran en un ángulo\(\theta\) alrededor de puntos en el eje neutro como se muestra en la Figura 1. Para rotaciones pequeñas, este ángulo viene dado aproximadamente por la\(x\) -derivada de la función de deflexión vertical del haz\(v(x)\) (La expresión exacta para curvatura es

\[\dfrac{d \theta}{ds} = \dfrac{d^2 v/dx^2}{[1 + (dv/dx)^2]^{3/2}}.\]

Esto da\(\theta \approx dv/dx\) cuando la derivada cuadrada en el denominador es pequeña en comparación con 1. ):

\[u = -y v_{,x}\]

donde la coma indica diferenciación con respecto a la variable indicada (\(v_{,x} \equiv dv/dx\)). Aquí\(y\) se mide positivo hacia arriba desde el eje neutro, cuya ubicación dentro del haz aún no se ha determinado.

Figura 1: Geometría de flexión de viga.

2. Ecuación cinemática: La deformación normal\(x\) -dirección\(\epsilon_x\) es entonces el gradiente del desplazamiento:

\[\epsilon_x = \dfrac{du}{dx} = -yv_{,xx}\]

Tenga en cuenta que las deformaciones son cero en el eje neutro donde\(y = 0\), negativas (compresivas) por encima del eje, y positivas (tracción) por debajo. Aumentan en magnitud linealmente con\(y\), tanto como las tensiones de cizallamiento aumentaron linealmente con\(r\) en un eje circular cargado torsionalmente. La cantidad\(v_{,xx} \equiv d^2v/dx^2\) es la tasa espacial de cambio de la pendiente de la curva de deflexión de la viga, la “pendiente de la pendiente”. A esto se le llama la curvatura de la viga.

3. Ecuación constitutiva: Las tensiones se obtienen directamente de la ley de Hooke como

\[\sigma_x = E\epsilon_x = -y Ev_{,xx}\]

Esto restringe la aplicabilidad de esta derivación a materiales elásticos lineales. De ahí que la tensión axial normal, al igual que la tensión, aumenta linealmente desde cero en el eje neutro hasta un máximo en las superficies exteriores de la viga.

4. Relaciones de equilibrio: Dado que no hay cargas axiales (\(x\)-dirección) aplicadas externamente a la viga, la fuerza axial total generada por las\(\sigma_x\) tensiones normales (mostrada en la Figura 2) debe ser cero. Esto se puede expresar como

\(\sum F_x = 0 = \int_A \sigma_x dA = \int_A -y Ev_{,xx} dA\)

lo que requiere que

\(\int_A y dA = 0\)

La distancia\(\bar{y}\) desde el eje neutro hasta el centroide del área de la sección transversal es

\(\bar{y} = \dfrac{\int_A y dA}{\int_A dA}\)

Por lo tanto\(\bar{y} = 0\), es decir, el eje neutro es coincidente con el centroide del área de la sección transversal del haz. Este resultado es obvio en la reflexión, ya que las tensiones aumentan a la misma velocidad lineal, por encima del eje en compresión y por debajo del eje en tensión. Solo si el eje está exactamente en la posición centroidal estas tensiones se equilibrarán para dar cero fuerza horizontal neta y mantener la viga en equilibrio horizontal.

Figura 2: Equilibrio de momento y fuerza en la viga.

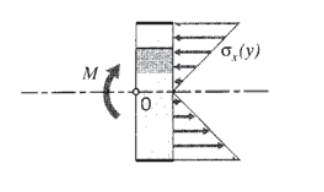
Las tensiones normales en compresión y tensión se equilibran para dar una fuerza horizontal neta cero, pero también producen un momento neto en el sentido de las agujas del reloj. Este momento debe igualar el valor de\(M(x)\) a ese valor de\(x\), como se ve tomando un momento de equilibrio alrededor del punto\(O\):

\(\sum M_O = 0 = M + \int_A \sigma_x \cdot y dA\)

\[M = \int_A (y Ev_{,xx}) \cdot y dA = Ev_{,xx} \int_A y^2 dA\]

Figura 3: Momento de inercia para una sección rectangular.

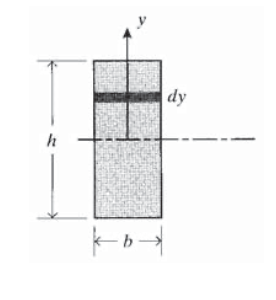
La cantidad\(\int y^2 dA\) es el momento rectangular de inercia con respecto al eje centroidal, denotado\(I\). Para una sección transversal rectangular de altura\(h\) y anchura\(b\) como se muestra en la Figura 3 esto es:

\[I = \int_{-h/2}^{h/2} y^2 b dy = \dfrac{bh^3}{12}\]

Resolviendo la ecuación 4.2.4 para\(v_{,xx}\), la curvatura del haz es

\[v_{,xx} = \dfrac{M}{EI}\]

5. Se puede obtener una fórmula explícita para el estrés usando esto en la Ecuación 4.2.3:

\[\sigma_x = -y E \dfrac{M}{EI} = \dfrac{-My}{I}\]

La expresión final para tensión, Ecuación 4.2.7, es similar a\(\tau_{\theta_z} = Tr/J\) la de los ejes circulares retorcidos: la tensión varía linealmente desde cero en el eje neutro hasta un máximo en la superficie exterior, varía inversamente con el momento de inercia de la sección transversal, y es independiente de los materiales propiedades. Así como un diseñador favorecerá los ejes de transmisión anulares para maximizar el momento polar de inercia\(J\), las vigas a menudo se hacen con bridas anchas en las superficies superior e inferior para aumentar\(I\).

Ejemplo\(\PageIndex{1}\): Cantilevered T-beam

Considere una viga en T en voladizo con dimensiones como se muestra en la Figura 4, llevando una carga uniforme de\(w N/m\). El momento máximo de flexión se produce en la pared, y se encuentra fácilmente para ser\(M_{\max} = (wL)(L/2)\). El estrés viene dado entonces por la Ecuación 4.2.7, que requiere que sepamos la ubicación del eje neutro (ya que\(y\) y\(I\) se miden a partir de ahí).

Figura 4: Una viga en T en voladizo.

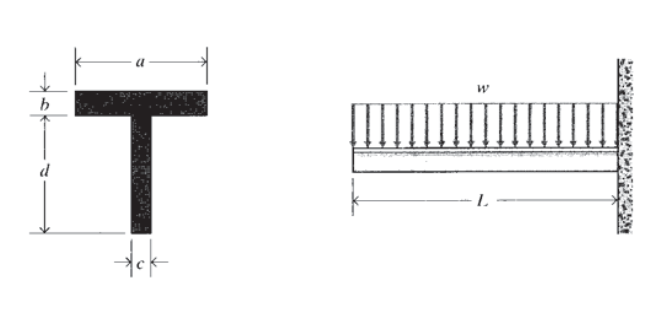
La distancia\(y\) desde la parte inferior de la viga hasta el eje neutro centroidal se puede encontrar usando el “teorema de área compuesta” (ver Ejercicio\(\PageIndex{1}\)). Este teorema establece que la distancia desde un eje arbitrario al centroide de un área conformada por varias subáreas es la suma de las subáreas por la distancia a sus centroides individuales, dividida por la suma de las subáreas (es decir, el área total):

\(\bar{y} = \dfrac{\sum_i A_i \bar{y}_i}{\sum_i A_i}\)

Para nuestro ejemplo, esto es

\(\bar{y} = \dfrac{(d/2)(cd) + (d + b/2)(ab)}{cd + ab}\)

Los momentos de inercia de las partes individuales del área compuesta con respecto a sus propios centroides son justos\(ab^3/12\) y\(cd^3/12\). Estos momentos pueden ser referenciados al eje horizontal a través del centroide del área compuesta usando el “teorema del eje paralelo” (ver Ejercicio\(\PageIndex{3}\)). Este teorema establece que el momento de inercia\(I_{z'}\) de un área\(A\), relativo a cualquier eje arbitrario\(z'\) paralelo a un eje a través del centroide pero a una\(d\) distancia de éste, es el momento de inercia relativo al eje centroidal\(I_z\) más el producto del área\(A\) y el cuadrado de la distancia\(d\):

\(I_{z'} = I_z + A d^2\)

Para nuestro ejemplo, esto es

El momento de inercia de toda el área compuesta, relativo a su centroide, es entonces la suma de estas dos contribuciones:

\(I = I^{(1)} + I^{(2)}\)

La tensión máxima viene dada por la Ecuación 4.2.7 utilizando este valor de\(I\) y\(y = \bar{y}/2\) (la distancia desde el eje neutro a las fibras externas), junto con el momento máximo de flexión\(M_{\max}\). El resultado de estas sustituciones es

\(\sigma_x = \dfrac{(3d^2c + 6abd + 3ab^2)wL^2}{2c^2d^4 + 8abcd^3 + 12ab^2cd^2 + 8ab^3cd + 2a^2b^4}\)

En la práctica, cada paso probablemente se reduciría a un valor numérico en lugar de trabajar hacia una solución algebraica.

En flexión pura (solo momentos de flexión aplicados, sin fuerzas transversales o longitudinales), la única tensión es la\(\sigma_x\) dada por la Ecuación 4.2.7. Todas las demás tensiones son cero (\(\sigma_y = \sigma_z = \tau_{xy} = \tau_{xz} = \tau_{yz} = 0\)). Sin embargo, otras cepas\(\epsilon_x\) están presentes, debido al efecto Poisson. Esto no genera deformación por cizallamiento\((\gamma_{xy} = \gamma_{xz} = \gamma_{yz} = 0)\), pero las cepas normales son

Las cepas también se pueden escribir en términos de curvaturas. De la Ecuación 4.2.2, la curvatura a lo largo de la viga es

\(v_{,xx} = -\dfrac{\epsilon_x}{y}\)

Esto va acompañado de una curvatura transversal al eje de la viga dada por

\(v_{,zz} = -\dfrac{\epsilon_z}{y} = \dfrac{\nu\epsilon_x}{y} = -\nu v_{,xx}\)

Esta curvatura transversal, mostrada en la Figura 5, se conoce como curvatura anticlástica; se puede observar doblando una goma de borrar tipo “Pink Pearl” en los dedos.

Figura 5: Curvatura anticlástica.

Al igual que con las estructuras de tensión y torsión, los problemas de flexión a menudo se pueden hacer más fácilmente con métodos de energía. Conociendo la tensión de la Ecuación 4.2.7, la energía de deformación debida a la tensión de flexión se\(U_b\) puede encontrar integrando la energía de deformación por unidad de volumen\(U^* = \sigma^2/2E\) sobre el volumen de la muestra:

\(U_b = \int_V U^* dV = \int_L \int_A \dfrac{\sigma_x^2}{2E} dA dL\)

\(= \int_L \int_A \dfrac{1}{2E} (\dfrac{-My}{I})^2 dA dL = \int_L \dfrac{M^2}{2EI^2} \int_A y^2 dAdL\)

Ya que\(\int_A y^2 dA = I\), esto se convierte en

\[U_b = \int_L \dfrac{M^2 dL}{2EI}\]

Si el momento de flexión es constante a lo largo de la viga (definitivamente no es el caso habitual), esto se convierte

\(U = \dfrac{M^2 L}{2EI}\)

Este es otro análogo a la expresión de tensión uniaxial,\(U = P^2L/2AE\).

pandeo

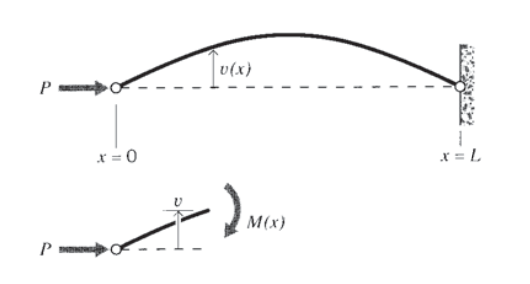
Las columnas largas y delgadas colocadas en compresión son propensas a fallar por pandeo, en el que la columna desarrolla una torcedura en algún lugar a lo largo de su longitud y colapsa rápidamente a menos que la carga se relaje Este es en realidad un fenómeno de flexión, impulsado por el momento de flexión que se desarrolla cuando y cuando la viga sufre una deflexión transversal. Considera una viga cargada en compresión axial y clavada en ambos extremos como se muestra en la Figura 6. Ahora que se haga que la viga se desvíe transversalmente en una cantidad v, tal vez por una carga lateral adventicia o incluso una irregularidad en la sección transversal de la viga. Las posiciones a lo largo de la viga experimentarán un momento dado por

\[M(x) = Pv(x)\]

La propia rigidez de la viga actuará para restaurar la deflexión y recuperar una forma recta, pero el efecto del momento de flexión es desviar más la viga. Es una batalla sobre la que gana la influencia. Si la tendencia del momento de flexión a aumentar la deflexión domina sobre la capacidad de la rigidez elástica de la viga para resistir la flexión, la viga se volverá inestable, continuando doblándose a una velocidad de aceleración hasta que falle.

Figura 6: Inminente pandeo en una viga.

El momento de flexión está relacionado con la curvatura del haz por la Ecuación 4.2.6, por lo que combinar esto con la Ecuación 4.2.9 da

\[v_{,xx} = \dfrac{P}{EI} v\]

Por supuesto, esta ecuación gobernante se satisface de manera idéntica si\(v = 0\), es decir, el haz es recto. Deseamos mirar más allá de esta solución trivial, y preguntar si la viga podría adoptar una forma doblada que satisfaga también la ecuación gobernante; esto implicaría que la rigidez es insuficiente para restaurar la forma no doblada, de manera que la viga comienza a doblarse. La ecuación 4.2.10 será satisfecha por funciones que sean proporcionales a sus propias segundas derivadas. Las funciones trigonométricas tienen esta propiedad, por lo que las soluciones candidatas serán de la forma

\(v = c_1 \sin \sqrt{\dfrac{P}{EI}} x + c_2 \cos \sqrt{\dfrac{P}{EI}} x\)

Es obvio que\(c_2\) debe ser cero, ya que la desviación debe ir a cero en\(x = 0\) y\(L\). Además, el término seno también debe ir a cero en estas dos posiciones, lo que requiere que la longitud\(L\) sea exactamente igual a un múltiplo de la media longitud de onda de la función sinusoidal:

\(\sqrt{\dfrac{P}{EI} L} = n\pi, n = 1, 2, 3, \cdots\)

El valor más bajo de\(P\) llevar a la forma deformada corresponde a\(n = 1\); la carga crítica de pandeo\(P_{cr}\) es entonces:

\[P_{cr} = \dfrac{\pi^2 EI}{L^2}\]

Tenga en cuenta la dependencia de\(L^2\), por lo que la carga de pandeo cae con el cuadrado de la longitud.

Esta fuerte dependencia de la longitud muestra por qué el travesaño es tan importante para prevenir el pandeo. Si se agrega una abrazadera en el punto medio de la viga como se muestra en la Figura 7 para eliminar la deflexión allí, la forma de pandeo se ve obligada a adoptar una longitud de onda de\(L\) más que 2\(L\). Esto equivale a hacer que la viga sea la mitad de larga, lo que aumenta la carga crítica de pandeo en un factor de cuatro.

Figura 7: Efecto del soporte lateral y las condiciones finales sobre el pandeo de la viga.

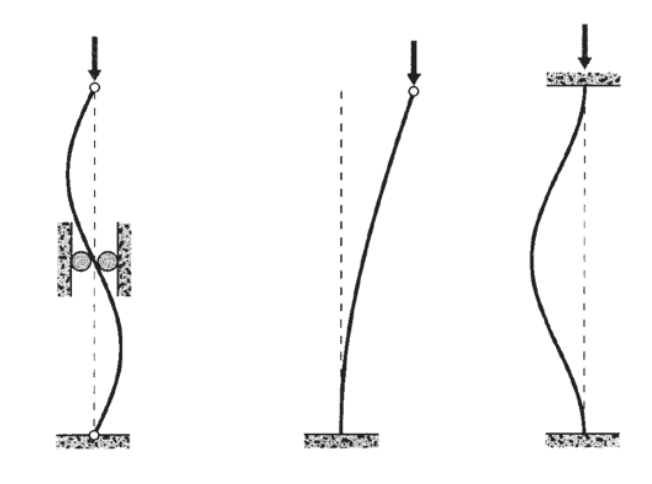
Razonamiento similar se puede utilizar para evaluar el resultado de tener diferentes condiciones de soporte. Si, por ejemplo, la viga está en voladizo en un extremo pero sin soporte en el otro, su forma de pandeo será un cuarto de onda sinusoidal. Esto equivale a hacer que la viga sea el doble de larga que la caja con ambos extremos clavados, por lo que la carga de pandeo disminuirá en un factor de cuatro. El voladizo de ambos extremos fuerza una forma de onda completa, con la misma carga de pandeo que la viga fija con un soporte de punto medio.

Esfuerzos cortantes

Las cargas transversales curvan las vigas induciendo tensiones normales de tracción axial y compresión en la\(x\) dirección de la viga, como se discutió anteriormente. Además, provocan efectos de cizallamiento que tienden a deslizarse planos verticales tangencialmente entre sí como se representa en la Figura 8, al igual que deslizar naipes uno junto al otro. Las tensiones\(\tau_{xy}\) asociadas con este efecto de corte se suman a la fuerza de corte vertical que hemos estado llamando\(V\), y ahora buscamos comprender cómo se distribuyen estas tensiones sobre la sección transversal de la viga. El esfuerzo cortante en planos verticales debe ir acompañado de un esfuerzo igual en planos horizontales ya que\(\tau_{xy} = \tau_{yx}\), y estos esfuerzos de cizallamiento horizontales deben llegar a ser cero en las superficies superior e inferior de la viga a menos que se aplique allí una tracción para equilibrarlos. De ahí que deban alcanzar un máximo en algún lugar dentro de la viga.

La variación de este esfuerzo cortante horizontal con la posición vertical y se puede determinar examinando un cuerpo libre de ancho\(dx\) cortado de la viga a una distancia y por encima del eje neutro como se muestra en la Figura 9. El momento en la cara vertical izquierda es\(M(x)\), y en la cara derecha ha aumentado a\(M + dM\). Dado que las tensiones normales horizontales son directamente proporcionales al momento (\(\sigma x = My/I\)), cualquier incremento en el momento dM sobre la distancia\(dx\) produce un desequilibrio en la fuerza horizontal derivado de las tensiones normales. Este desequilibrio debe ser compensado por un esfuerzo cortante\(\tau_{xy}\) en el plano horizontal en\(y\). El balance de fuerza horizontal se escribe como

\(\tau_{xy} b dx = \int_{A'} \dfrac{dM \xi}{I} dA'\)

Figura 8: Desplazamientos de cizallamiento en flexión de viga.

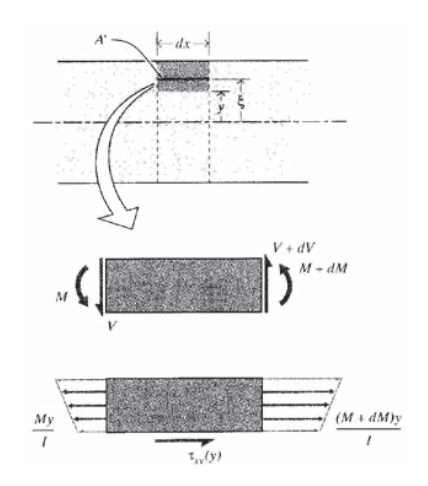
Figura 9: Momento de cizallamiento y flexión en una longitud diferencial de viga.

donde\(b\) es el ancho de la viga en\(y, \xi\) es una variable de altura ficticia que va desde\(y\) la superficie exterior de la viga, y\(A'\) es el área de sección transversal entre el plano en\(y\) y la superficie exterior. Usando\(dM = V\ dx\) de la Ecuación 4.2.8 del Módulo 12, esto se convierte en

\[\tau_{xy} = \dfrac{V}{Ib} \int_A' \xi dA' = \dfrac{VQ}{Ib}\]

donde aquí\(Q(y) = \int_{A'} \xi dA' = \bar{\xi} A'\) está el primer momento del área arriba\(y\) alrededor del eje neutro.

Figura 10: Sección de una viga rectangular.

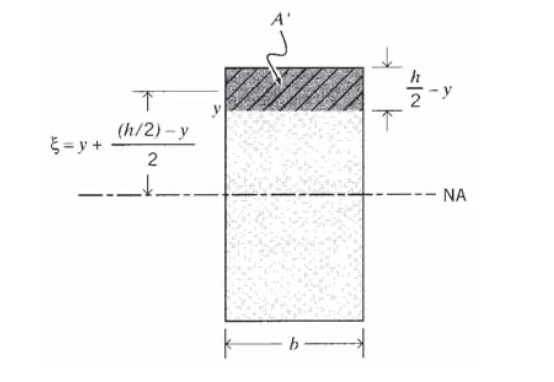
El parámetro\(Q(y)\) es conocido por confundir a personas nuevas en la teoría del haz. Para determinarlo para una altura dada\(y\) con relación al eje neutro, comience por esbozar la sección transversal de la viga, y dibuje una línea de línea horizontal en la posición\(y\) en la que\(Q\) se busca (La Figura 10 muestra una viga rectangular de ancho\(b\) y alto constantes\(h\) para ilustración). Anote el área\(A'\) entre esta línea y la superficie exterior (indicada por rayado cruzado en la Figura 10). Ahora calcule la distancia\(\bar{\xi}\) desde el eje neutro hasta el centroide de\(A'\). El parámetro\(Q(y)\) es producto de\(A'\) y\(\xi\); este es el primer momento del área\(A'\) con respecto al eje centroidal. Para la viga rectangular, es

Obsérvese que\(Q(y)\), y por tanto\(\tau_{xy}(y)\) también, es parabólico, siendo máximo en el eje neutro (\(y\)= 0) y cero en la superficie exterior (\(y = h/2\)). Usando\(I = bh^3/12\) para la viga rectangular, el esfuerzo cortante máximo dado por la Ecuación 4.2.12 es

\(\tau_{xy, \max} = \tau_{xy}|_{y = 0} = \dfrac{3V}{2bh}\)

(Tenga en cuenta que las dos expresiones anteriores para\(Q\) y\(\tau_{xy,\max}\) son solo para sección transversal rectangular; las secciones de otras formas tendrán resultados diferentes). Estos esfuerzos cortantes son los más importantes en vigas que son cortas con relación a su altura, ya que el momento de flexión suele aumentar con la longitud y la fuerza de cizallamiento no (ver Ejercicio\(\PageIndex{11}\)). Una prueba estándar para la resistencia al corte interlaminar (“Resistencia aparente al corte horizontal de plásticos reforzados por método de viga corta”, ASTM D2344, Sociedad Americana de Pruebas y Materiales.) es colocar una viga corta en flexión y observar la carga a la que se desarrollan grietas a lo largo del plano medio.

Ejemplo\(\PageIndex{2}\)

Dado que el esfuerzo normal es máximo donde el esfuerzo cortante horizontal es cero (en las fibras externas), y el esfuerzo cortante es máximo donde el esfuerzo normal es cero (en el eje neutro), a menudo es posible considerarlos uno a la vez. Sin embargo, la unión del alma y la brida en vigas I y T suele ser un lugar de especial interés, ya que aquí ambas tensiones pueden tomar valores sustanciales.

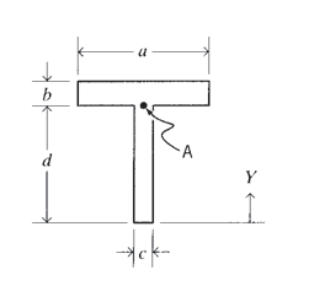
Considera la viga en T vista previamente en el Ejemplo\(\PageIndex{1}\), y examina la ubicación en el punto\(A\) mostrado en la Figura 11, en la web inmediatamente por debajo de la brida. Aquí el ancho\(b\) en la Ecuación 4.2.12 es la dimensión etiquetada\(c\); dado que la viga es delgada aquí el esfuerzo cortante\(\tau_{xy}\) tenderá a ser grande, pero caerá dramáticamente en la brida a medida que el ancho salta al valor mayor a. la tensión normal en el punto\(A\) se calcula a partir de \(\sigma_x = My/I\), utilizando\(y = d − y\). Este valor será casi tan grande como la tensión de la fibra externa si el grosor de la brida b es pequeño en comparación con la altura de la red\(d\). El círculo de Mohr para el estado de tensión en el punto\(A\) tendría entonces contribuciones apreciables de ambos\(\sigma_x\) y\(\tau_{xy}\), y puede resultar en una tensión principal mayor que en las fibras externas o el eje neutro.

Este problema proporciona una buena revisión de las relaciones de gobierno para tensiones normales y cortantes en vigas, y también es una aplicación natural para métodos informáticos de manipulación simbólica. Usando el software Maple, podríamos comenzar por calcular la ubicación del eje centroidal:

Figura 11: Sección de viga en T.

Aquí el símbolo “>” es el símbolo Maple, y Maple necesita el “;” para finalizar el comando. La fuerza cortante máxima y el momento de flexión (presentes en la pared) se definen en términos de la carga distribuida y la longitud de la viga como

> ybar := ((d/2)*c*d) + ( (d+(b/2) )*a*b )/( c*d + a*b );  

Para propósitos de trazado, será conveniente tener una variable de altura Y medida desde la parte inferior de la sección. Las relaciones para la tensión normal, la tensión cortante y la primera tensión principal son funciones de Y; estas se definen mediante el comando “procedimiento” de Maple:

> V := w*L;
> M := -(w*L)*(L/2); 

Para propósitos de trazado, será conveniente tener una variable de altura Y medida desde la parte inferior de la sección. Las relaciones para la tensión normal, la tensión cortante y la primera tensión principal son funciones de Y; estas se definen mediante el comando “procedimiento” de Maple:

> sigx := proc (Y) -M*(Y-ybar)/Iz end;
> tauxy := proc (Y) V*Q(Y)/(Iz*B(Y) ) end;
> sigp1 := proc (Y) (sigx(Y)/2) + sqrt( (sigx(Y)/2)^2 + (tauxy(Y))^2 ) end; 

El momento de inercia Iz se calcula como

> I1 := (a*b^3)/12 + a*b* (d+(b/2)-ybar)^2; 
> I2 := (c*d^3)/12 + c*d* ((d/2)-ybar)^2;
> Iz := I1+I2; 

El ancho de viga B se define para tomar el valor apropiado dependiendo de si la variable Y está en el alma o en la brida:

> B:= proc (Y) if Y<d then B:=c else B:=a fi end; 

El comando “fi” (“if” deletreado al revés) se utiliza para terminar un bucle if-then. La función Q (Y) se define para el alma y la brida por separado:

> Q:= proc (Y) if Y<d then
>      int( (yy-ybar)*c,yy=Y..d) + int( (yy-ybar)*a,yy=d..(d+b) )
>    else
>      int( (yy-ybar)*a,yy=Y.. (d+b) ) 
>    fi end;

Aquí “int” es el comando Maple para la integración, y yy se usa como la variable de altura ficticia. Los valores numéricos de los diversos parámetros se definen como

> a:=3: b:=1/4: c:=1/4: d:=3-b: L:=8: w:=100: 

Figura 12: Tensiones en la unión de brida de alma en una viga corta en T en voladizo sometida a carga uniforme.

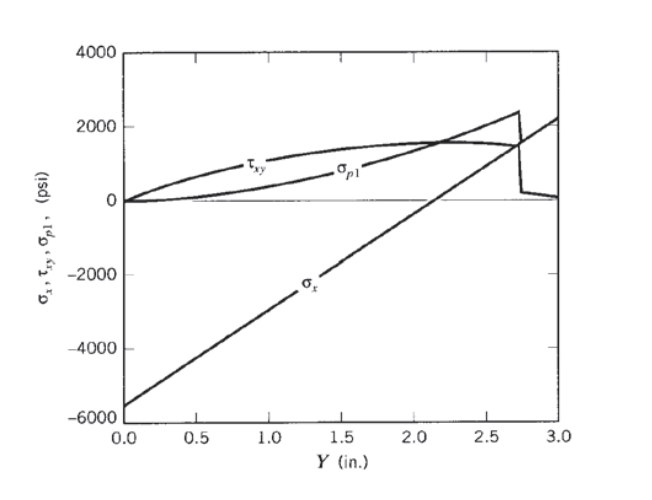
Finalmente, las tensiones se pueden graficar usando el comando Maple plot

> plot({sigx,tauxy,sigp1},Y=0..3,sigx=-500..2500); 

La gráfica resultante se muestra en la Figura 12.

Ejemplo\(\PageIndex{3}\)

En el ejemplo anterior, nos interesó la variación de la tensión en función de la altura en una viga de sección transversal irregular. Otro problema común de diseño o análisis es el de la variación de la tensión no solo en función de la altura sino también de la distancia a lo largo de la dimensión de envergadura de la viga. Los momentos de cizallamiento y flexión\(V(x)\) y\(M(x)\) varían a lo largo de esta dimensión, y así naturalmente hacen las tensiones\(\sigma_x (x,y)\) y\(\tau_{xy} (x,y)\) que dependen de ellas según las Ecuaciones 4.2.7 y 4.2.12.

Figura 13: (a) Viga en flexión de cuatro puntos. (b) Diagrama de cuerpo libre.

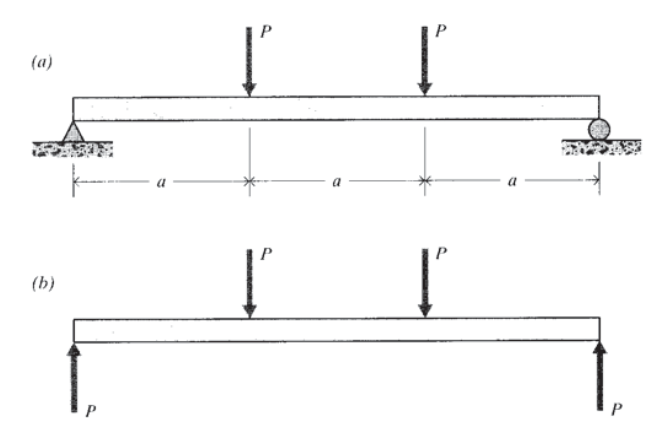
Considera una viga corta de sección transversal rectangular sometida a carga de cuatro puntos como se ve en la Figura 13. Las funciones de carga, cizallamiento y momento de flexión son:

Las tensiones cortantes y normales se pueden determinar como funciones de\(x\) y\(y\) directamente a partir de estas funciones, así como parámetros tales como la tensión principal. Dado que\(\sigma_y\) es cero en todas partes, el estrés principal es

\(\sigma_{p1} = \dfrac{\sigma_x}{2} + \sqrt{(\dfrac{\sigma_x}{2})^2 + \tau_{xy}^2}\)

Una forma de visualizar la variación x-y de\(\sigma_{p1}\) es mediante una gráfica de superficie 3D, que puede ser preparada fácilmente por Maple. Para los valores numéricos\(P = 100, a = h = 10, b = 3\), podríamos usar las expresiones (Respuestas de arce eliminadas por brevedad):

> # use Heaviside for singularity functions
> readlib(Heaviside);
> sfn := proc(x,a,n) (x-a)^n * Heaviside(x-a) end;
> # define shear and bending moment functions
> V:=(x)-> -P*sfn(x,0,0)+P*sfn(x,a,0)+P*sfn(x,2*a,0)-P*sfn(x,3*a,0); 
> M:=(x)-> P*sfn(x,0,1)-P*sfn(x,a,1)-P*sfn(x,2*a,1)+P*sfn(x,3*a,1); 
> # define shear stress function
> tau:=V(x)*Q/(Iz*b);
> Q:=(b/2)*( (h^2/4) -y^2);
> Iz:=b*h^3/12;
> # define normal stress function
> sig:=M(x)*y/Iz;
> # define principal stress
> sigp:= (sig/2) + sqrt( (sig/2)^2 + tau^2 );
> # define numerical parameters
> P:=100;a:=10;h:=10;b:=3;
> # make plot
> plot3d(sigp,x=0..3*a,y=-h/2 .. h/2); 

La gráfica resultante se muestra en la Figura 14. El dominio del esfuerzo cortante parabólico es evidente cerca de los extremos de la viga, ya que aquí la fuerza de cizallamiento está en su valor máximo pero el momento de flexión es pequeño (graficar los diagramas de cizallamiento y momento de flexión para confirmarlo). En la parte central de la viga, donde\(a < x < 2a\), la fuerza cortante se desvanece y la tensión principal se rige solo por la tensión normal\(\sigma_x\), la cual varía linealmente del eje neutro de la viga. La primera tensión principal es cero en la parte inferior compresiva de esta sección, ya que aquí la tensión normal\(\sigma_x\) es negativa y el borde derecho del círculo de Mohr debe pasar por el valor cero de la otra tensión normal\(\sigma_y\). Trabajar a través de la gráfica de la Figura 14 es una buena revisión de las fórmulas de tensión del haz.

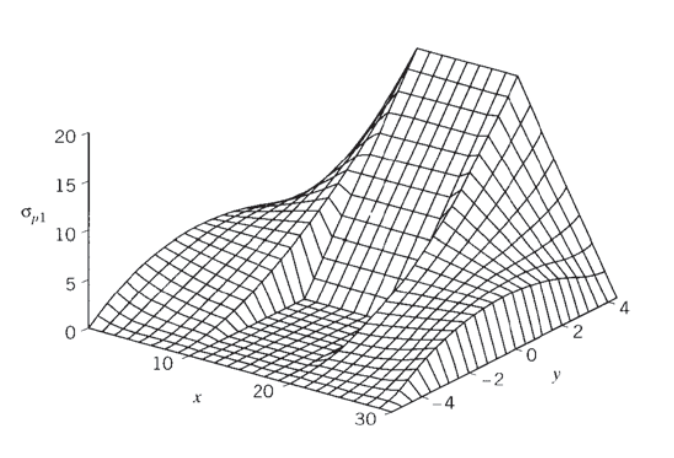
Figura 14: Variación de la tensión principal\(\sigma_{p1}\) en flexión de cuatro puntos.

Ejercicio\(\PageIndex{1}\)

Derivar el teorema del área compuesta para determinar el centroide de un área compuesta.

\(\bar{y} = \dfrac{\sum_i A_i \bar{y}_i}{\sum_i A_i}\)

Ejercicio\(\PageIndex{2}\)

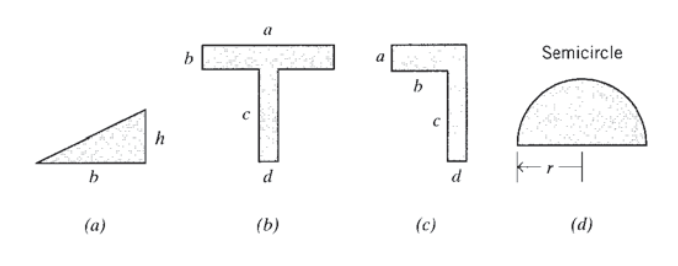
(a) - (d) Localizar los centroides de las áreas mostradas.

Ejercicio\(\PageIndex{3}\)

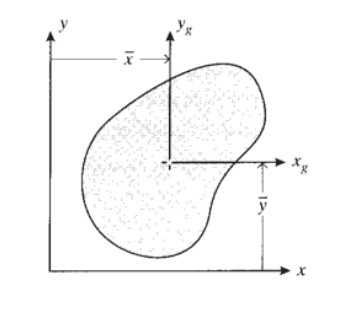
Derivar el “teorema de eje paralelo” para los momentos de inercia de un área plana:

\(I_x = I_{xg} + A \bar{y}^2\)

\(I_y = I_{yg} + A \bar{x}^2\)

Ejercicio\(\PageIndex{4}\)

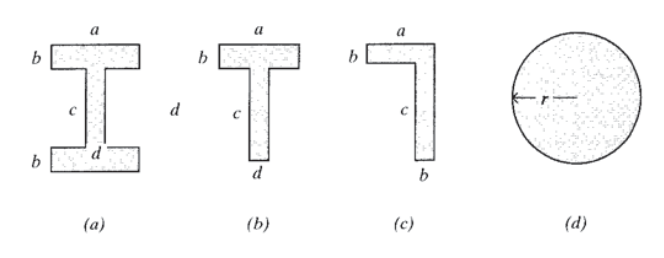
(a) - (d) Determinar el momento de inercia relativo al eje centroidal horizontal de las áreas mostradas.

Ejercicio\(\PageIndex{5}\)

Demostrar que el momento de inercia se transforma con respecto a las rotaciones de los ejes exactamente como lo hace la tensión:

donde\(I_x\) y\(I_y\) son los momentos de inercia relativos a los\(y\) ejes\(x\) y respectivamente y\(I_{xy}\) es el producto de inercia definido como

\(I_{xy} = \int_A xy dA\)

Ejercicio\(\PageIndex{6}\)

(a) — (h) Determinar la máxima tensión normal σx en los haces aquí mostrados, utilizando los valores (según sea necesario)\(L = 25\ in\),\(a = 5 \ in\),\(w = 10\ lb/in\),\(P = 150\ lb\). Asumir una sección transversal rectangular\(b = 1\) de ancho y alto\(h = 2\ in\).

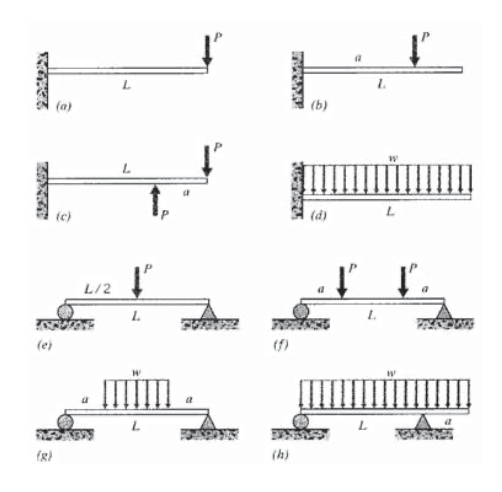
Ejercicio\(\PageIndex{7}\)

Justifica la declaración en la prueba ASTM D790, “Métodos de prueba estándar para las propiedades de flexión de plásticos no reforzados y reforzados y materiales aislantes eléctricos”, que dice:

Cuando una viga de material homogéneo y elástico se prueba en flexión como una viga simple soportada en dos puntos y cargada en el punto medio, la tensión máxima en las fibras externas se produce en la mitad del tramo. Esta tensión puede calcularse para cualquier punto de la curva carga-deflexión mediante la siguiente ecuación:

\(S = 3PL/2bd^2\)

donde\(S\) = tensión en las fibras externas a la mitad del tramo, MPa;\(P\) = carga en un punto dado en la curva carga-deflexión;\(L\) = tramo de soporte, mm;\(b\) = ancho de la viga ensayada, mm; y d = profundidad de la viga ensayada, mm.

Ejercicio\(\PageIndex{8}\)

Justifica la declaración en la prueba ASTM D790, “Métodos de prueba estándar para las propiedades de flexión de plásticos no reforzados y reforzados y materiales aislantes eléctricos”, que dice:

El módulo tangente de elasticidad, a menudo llamado el “módulo de elasticidad”, es la relación, dentro del límite elástico de tensión a la deformación correspondiente y se expresará en megapascales. Se calcula dibujando una tangente a la porción inicial de línea recta más empinada de la curva de carga-deflexión y usando [la expresión:]

\(E_b = L^3 m/4bd^3\)

donde\(E_b\) = módulo de elasticidad en flexión, MPa;\(L\) = tramo de soporte, mm;\(d\) = profundidad de la viga ensayada, mm; y\(m\) = pendiente de la tangente a la porción inicial de línea recta de la curva carga-deflexión,\(N/mm\) de deflexión.

Ejercicio\(\PageIndex{9}\)

Una viga rectangular se va a fresar a partir de material circular como se muestra. ¿Cuál debería ser la relación entre la altura y la anchura\((b/h)\) para minimizar las tensiones cuando la viga se dobla?

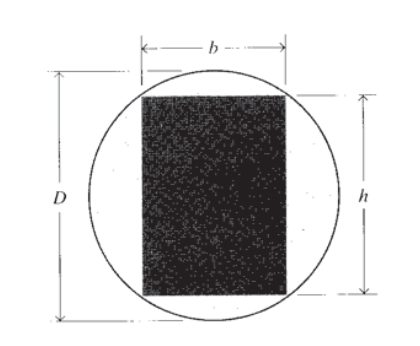
Ejercicio\(\PageIndex{10}\)

(a) - (h) Determinar la máxima cizalla τxy en las vigas de Ejercicio\(\PageIndex{6}\),, utilizando los valores (según sea necesario)\(L = 25\ in, a = 5\ in, w = 10\ lb/in, P = 150\ lb\). Asumir una sección transversal rectangular\(b = 1\) de ancho y alto\(h = 2\ in\).

Ejercicio\(\PageIndex{11}\)

Demostrar que la relación entre el esfuerzo de corte máximo y el esfuerzo normal máximo en una viga sometida a flexión de 3 puntos es

\(\dfrac{\tau}{\sigma} = \dfrac{h}{2L}\)

De ahí que la importancia del esfuerzo cortante aumente a medida que la viga se acorta en comparación con su altura.

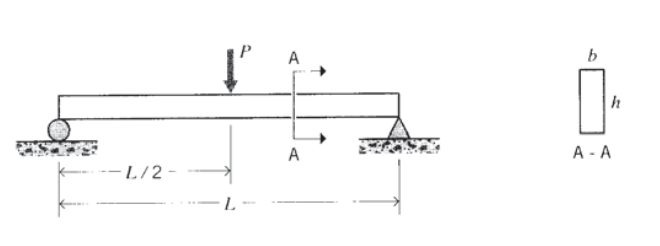
Ejercicio\(\PageIndex{12}\)

Lea la prueba ASTM D4475, “Método de prueba estándar para la resistencia al cizallamiento horizontal aparente de varillas de plástico reforzadas pultruidas por el método de viga corta” y justifique la expresión dada allí para la resistencia aparente al cizallamiento:

\(S = 0.849 P/d^2\)

donde\(S\) = resistencia aparente al cizallamiento\(N/m^2\),, (o psi);\(P\) = carga de rotura,\(N\), (o lbf); y\(d\) = diámetro del espécimen, m (o pulg.).

Ejercicio\(\PageIndex{13}\)

Para la viga en T que se muestra aquí, con dimensiones\(L = 3, a = 0.05, b = 0.005, c = 0.005, d = 0.7\) (all in\(m\)) y una distribución de carga de\(w = 5000 N/m\), determinar el esfuerzo de corte principal y máximo en el punto\(A\).

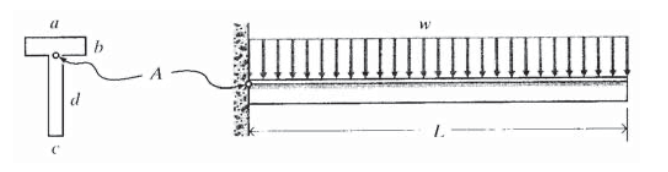
Ejercicio\(\PageIndex{14}\)

Determinar la tensión normal máxima en una viga en voladizo de sección transversal circular cuyo radio varía linealmente de\(4r_0\) a\(r_0\) en una distancia\(L\), cargada con una fuerza\(P\) en el extremo libre.

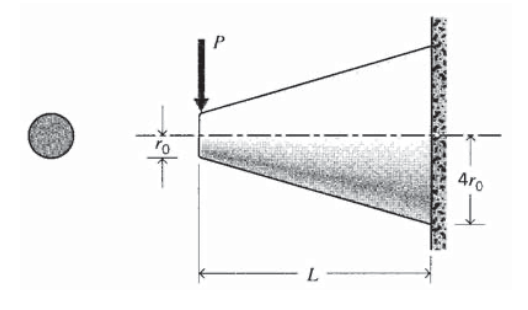
Ejercicio\(\PageIndex{15}\)

Una columna de acero al carbono tiene una longitud\(L = 1\ m\) y una sección transversal circular de diámetro\(d = 20\ mm\). Determinar la carga crítica de pandeo\(P_c\) para el caso de (a) ambos extremos clavados, (b) un extremo en voladizo, (c) ambos extremos clavados pero soportados lateralmente en el punto medio.

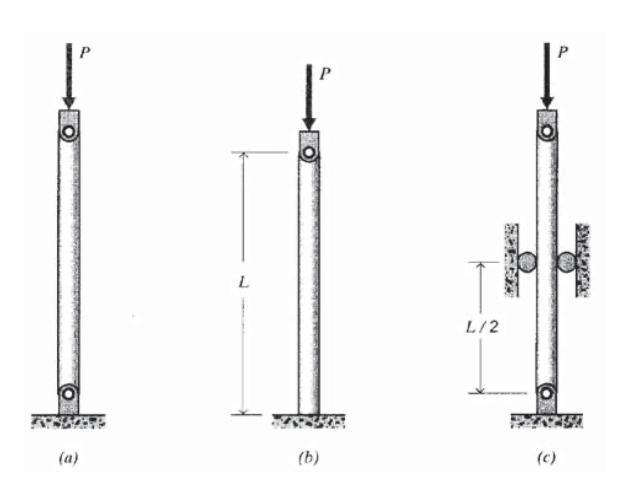
Ejercicio\(\PageIndex{16}\)

Una columna de acero al carbono tiene una longitud\(L = 1\ m\) y una sección transversal circular. Determinar el diámetro\(d\) en el que la columna tiene igual probabilidad de pandeo o rendimiento en compresión.