5.1: Soluciones de Forma Cerrada

Introducción

Durante la mayor parte de su desarrollo histórico, la ciencia de la Mecánica de Materiales se basó principalmente en teóricos matemáticos de forma cerrada (no computacional). Gran parte de su trabajo representa la intuición matemática y la habilidad de un orden muy alto, desafiando incluso para los investigadores avanzados de hoy. Esta teoría se imparte principalmente en asignaturas de posgrado, pero se esboza aquí tanto para proporcionar algunos antecedentes que serán útiles en el Módulo sobre Fractura como como introducción preliminar a estas materias más avanzadas.

Ecuaciones de gobierno

Anteriormente hemos mostrado (ver Módulo 9) cómo los gradientes espaciales de las seis tensiones de Cauchy están relacionados por tres ecuaciones de equilibrio que pueden escribirse en forma de pseudovector como

\[L^T \sigma = 0\]

Estas son aumentadas por seis ecuaciones constitutivas que se pueden escribir para materiales elásticos lineales como (ver Módulo 11)

\[\sigma = D \epsilon\]

y seis ecuaciones cinemáticas o de desplazamiento de tensión (Módulo 8)

\[\sigma = Lu\]

Estas quince ecuaciones deben ser satisfechas por las quince funciones independientes (tres desplazamientos\(u\), seis\(\epsilon\) deformaciones y seis tensiones\(\sigma\)). Estas funciones también deben satisfacer las condiciones de límite en el desplazamiento

\[u = \hat{u} \text{ on } \Gamma_u\]

donde\(\Gamma_u\) está la porción del límite en la que\(u = \hat{u}\) se prescriben los desplazamientos. El resto del límite debe entonces haber prescrito tracciones\(T = \hat{T}\), sobre las cuales las tensiones deben satisfacer la relación de Cauchy:

\[\sigma \hat{n} = \hat{T} \text{ on } \Gamma_T\]

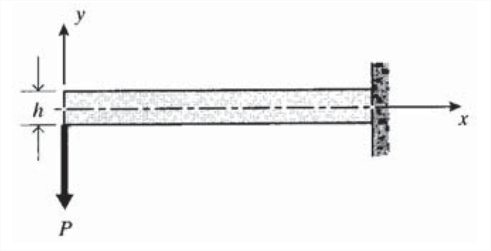
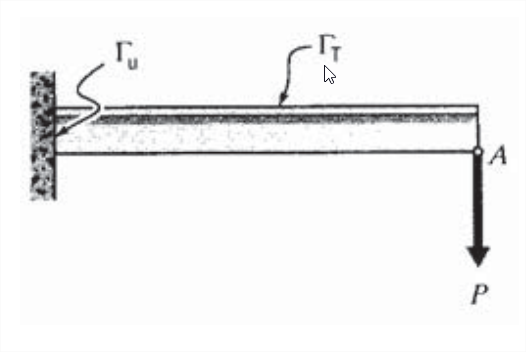
En la viga familiar en voladizo que se muestra en la Figura\(\PageIndex{1}\), la región de la viga en la pared constituye\(\Gamma_u\), habiendo especificado (cero) desplazamiento y pendiente. Todos los demás puntos en el límite de la viga conforman\(\Gamma_T\), con una carga de\(P\) en el punto de carga\(A\) y una carga especificada de cero en otra parte.

Figura\(\PageIndex{1}\): Viga en voladizo.

Con estructuras como la viga que tienen geometrías simples, se pueden obtener soluciones por el método directo que hemos utilizado en módulos anteriores: se escribe una expresión para los desplazamientos, a partir de la cual se pueden obtener las deformaciones y tensiones, y luego las tensiones se equilibran contra las cargas aplicadas externamente. (\(\PageIndex{2}\)El ejercicio proporciona otro ejemplo de este proceso.) En situaciones que no tengan esta simplicidad geométrica, el analista debe llevar a cabo una solución matemática, buscando funciones de tensión, deformación y desplazamiento que satisfagan tanto las ecuaciones gobernantes como las condiciones límite.

Actualmente, es probable que los problemas prácticos se resuelvan por aproximación computacional, pero casi siempre es preferible obtener una solución de forma cerrada si es posible. El resultado matemático mostrará la importancia funcional de los diversos parámetros, como las condiciones de carga o las propiedades del material, de una manera que una solución numérica no puede, y por lo tanto es más útil para guiar las decisiones de diseño. Por esta razón, el diseñador siempre debe comenzar un análisis de las estructuras portantes buscando soluciones de forma cerrada del problema dado, o similar,. Se encuentran disponibles varios compendios de tales soluciones, siendo el libro de Roark (W.C. Young, Roark's Formulas for Stress and Strain, McGraw-Hill, New York, 1989.) un ejemplo útil.

Sin embargo, siempre existe el peligro de realizar este tipo de “ingeniería de manuales” ciegamente, y esta sección está destinada en parte a ilustrar los conceptos matemáticos que subyacen a muchas de estas soluciones publicadas. Probablemente sea cierto que la mayoría de los problemas que se pueden resolver matemáticamente ya se han completado; estos son los problemas clásicos de la mecánica aplicada, y a menudo requieren un nivel bastante alto de sofisticación matemática. El texto clásico de Timoshenko y Goodier (S. Timoshenko y J.N. Goodier, Theory of Elasticidad, McGraw-Hill, Nueva York, 1951.) es una excelente fuente para seguir leyendo en esta área.

La función Airy stress

La expansión de las ecuaciones cinemáticas o de desplazamiento de tensión (Ecuación 5.1.3) en dos dimensiones da las formas familiares:

\[\begin{array} {rcl} {\epsilon_x} & = & {\dfrac{\partial u}{\partial x}} \\ {\epsilon_y} & = & {\dfrac{\partial v}{\partial y}} \\ {\gamma_{xy}} & = & {\dfrac{\partial v}{\partial x} + \dfrac{\partial u}{\partial y}} \end{array}\]

Dado que tres cepas\((\epsilon_x, \epsilon_y, \gamma_{xy})\) se escriben en términos de sólo dos desplazamientos\((u,v)\), no pueden especificarse arbitrariamente; debe existir una relación entre las tres cepas. Si\(\epsilon_x\) se diferencia dos\(dx, \epsilon_y\) veces por dos veces por\(dy\),\(dx\) y\(\gamma_{xy}\) por y luego\(dy\) tenemos directamente

\[\dfrac{\partial^2 \epsilon_x}{\partial y^2} + \dfrac{\partial^2 \epsilon_y}{\partial x^2} = \dfrac{\partial^2 \gamma_{xy}}{\partial x \partial y}\]

Para que los desplazamientos sean tan diferenciables, deben ser funciones continuas, lo que significa físicamente que el cuerpo debe deformarse de manera compatible, es decir, sin desarrollar grietas o solapamientos. Por esta razón, a la Ecuación 5.1.7 se le llama la ecuación de compatibilidad para cepas, ya que se garantiza la continuidad del cuerpo si las cepas lo satisfacen.

La ecuación de compatibilidad se puede escribir en términos de las tensiones en lugar de las deformaciones recordando las ecuaciones constitutivas para la tensión plana elástica:

\[\begin{array} {c} {\epsilon_x = \dfrac{1}{E} (\sigma_x - v \sigma_y)} \\ {\epsilon_y = \dfrac{1}{E} (\sigma_y - v \sigma_x)} \\ {\gamma_{xy} = \dfrac{1}{G} \tau_{xy} = \dfrac{2(1 + v)}{E} \tau_{xy}} \end{array}\]

Sustituyendo estos en la Ecuación 5.1.7 da

\[\dfrac{\partial^2}{\partial y^2} (\sigma_x - v \sigma_y) + \dfrac{\partial^2}{\partial x^2} (\sigma_y - v \sigma_x) = 2 (1 + v) \dfrac{\partial^2 \tau_{xy}}{\partial x \partial y}\]

Las tensiones que satisfacen esta relación garantizan la compatibilidad de la deformación.

Las tensiones también deben satisfacer las ecuaciones de equilibrio, que en dos dimensiones se pueden escribir

\(\dfrac{\partial \sigma_x}{\partial x} + \dfrac{\partial \tau_{xy}}{\partial y} = 0\)

\[\dfrac{\partial \tau_{xy}}{\partial x} + \dfrac{\partial \sigma_y}{\partial y} = 0\]

Como medio de simplificar la búsqueda de funciones cuyas derivadas obedecen a estas reglas, G.B. Airy (1801—1892) definió una función\(\phi\) de estrés a partir de la cual las tensiones podrían obtenerse por diferenciación:

\[\begin{array} {rcl} {\sigma_x} & = & {\dfrac{\partial^2 \phi}{\partial y^2}} \\ {\sigma_y} & = & {\dfrac{\partial^2 \phi}{\partial x^2}} \\ {\tau_{xy}} & = & {-\dfrac{\partial^2 \phi}{\partial x \partial y}} \end{array}\]

La sustitución directa mostrará que las tensiones obtenidas de este procedimiento satisfarán automáticamente las ecuaciones de equilibrio. Esta maniobra se limita esencialmente a problemas bidimensionales, pero con esa condición proporciona una gran simplificación en la búsqueda de funciones válidas para las tensiones.

Ahora sustituyendo estos en la Ecuación 5.1.9, tenemos

\[\dfrac{\partial^4 \phi}{\partial x^4} + 2\dfrac{\partial^4 \phi}{\partial x^2 \partial y^2} + \dfrac{\partial^4 \phi}{\partial y^4} \equiv \nabla^2(\nabla^2 \phi) \equiv \nabla^4 \phi = 0\]

Cualquier función\(\phi (x, y)\) que satisfaga esta relación satisfará las relaciones gobernantes para equilibrio, compatibilidad geométrica y elasticidad lineal. Por supuesto, se podrían escribir muchas funciones que satisfagan la ecuación de compatibilidad; por ejemplo, la configuración siempre\(\phi = 0\) funcionaría. Pero para que la solución sea correcta para un análisis de tensión particular, también deben satisfacerse las condiciones límite sobre el estrés y el desplazamiento. Esta suele ser una empresa mucho más difícil, y no existe una solución general que funcione para todos los casos. Se puede demostrar, sin embargo, que una solución que satisfaga tanto la ecuación de compatibilidad como las condiciones límite es única; es decir, que es la única solución correcta.

Tensiones alrededor de un orificio circular

Figura\(\PageIndex{2}\): Orificio circular en una placa con tensión uniaxial

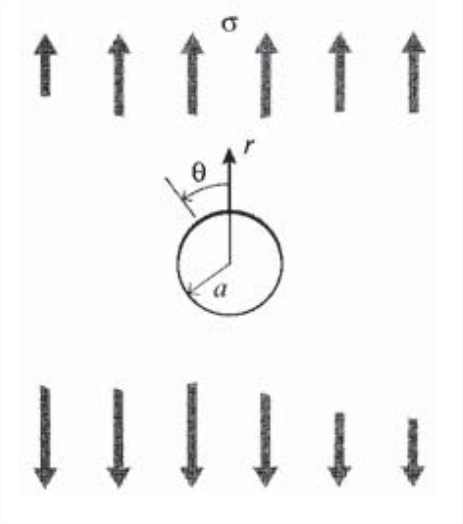
Para ilustrar el uso del enfoque de la función Airy, esbozaremos el importante trabajo de Kirsch (G. Kirsch, VDI, vol. 42, 1898; descrito en Timoshenko & Goodier, op. cit..), quien obtuvo una solución para la influencia en las tensiones de un agujero colocado en el material. Esto es de vital importancia en el análisis de problemas tales como los agujeros de remache utilizados en la unión, y el efecto de un vacío de fabricación en la falla inicial. Considera una lámina delgada como se ilustra en la Figura\(\PageIndex{2}\), infinita en dimensiones laterales pero que contiene un orificio circular de radio\(a\), y sometida a una tensión uniaxial\(\sigma\). Usando\(r, \theta\) coordenadas circulares centradas en el agujero, la ecuación de compatibilidad para\(\phi\) es

\[\nabla^4 \phi = (\dfrac{\partial^2}{\partial r^2} + \dfrac{1}{r}\dfrac{\partial}{\partial r} + \dfrac{1}{r^2}\dfrac{\partial^2}{\partial \theta^2}) (\dfrac{\partial^2 \phi}{\partial r^2} + \dfrac{1}{r}\dfrac{\partial \phi}{\partial r} + \dfrac{1}{r^2}\dfrac{\partial^2 \phi}{\partial \theta^2}) = 0\]

En estas coordenadas circulares, las tensiones se obtienen de\(\phi\) como

\[\begin{array} {rcl} {\sigma_r} & = & {\dfrac{1}{r}\dfrac{\partial \phi}{\partial r} + \dfrac{1}{r^2}\dfrac{\partial^2 \phi}{\partial \theta^2}} \\ {\sigma_{\theta}} & = & {\dfrac{\partial^2 \phi}{\partial r^2}} \\ {\tau_{r\theta}} & = & {-\dfrac{\partial}{\partial r} (\dfrac{1}{r} \dfrac{\partial \phi}{\partial \theta})} \end{array}\]

Ahora buscamos una función\(\phi (r, \theta)\) que satisfaga la Ecuación 5.1.13 y también las condiciones límite del problema. En la periferia del agujero los esfuerzos radiales y de cizallamiento deben desaparecer, ya que allí no existen tracciones externas:

\[\sigma_r = \tau_{r \theta} = 0, r = a\]

Lejos del agujero, las tensiones deben convertirse en el valor de campo lejano\(\sigma\); el procedimiento Mohr da los componentes de tensión radial y tangencial en coordenadas circulares como

\[\left \{ \begin{array} {rcl} {\sigma_r} & = & {\tfrac{\sigma}{2}(1 + \cos 2 \theta)} \\ {\sigma_{\theta}} & = & {\tfrac{\sigma}{2} (1 - \cos 2 \theta)} \\ {\tau_{r\theta}} & = & {\tfrac{\sigma}{2} \sin 2 \theta} \end{array} \right\} r \to \infty\]

Dado que las tensiones normales varían circunferencialmente como\(\cos 2\theta\) (eliminando temporalmente el\(\sigma/2\) factor) y las tensiones de cizalladura varían como\(\sin 2\theta\), una función de tensión aceptable podría ser de la forma

\[\phi = f(r) \cos 2 \theta\]

Cuando esto se sustituye en la Ecuación 5.1.13,\(f(r)\) se obtiene una ecuación diferencial ordinaria en:

\[\left(\frac{d^{2}}{d r^{2}}+\frac{1}{r} \frac{d}{d r}-\frac{4}{r^{2}}\right)\left(\frac{d^{2} f}{d r^{2}}+\frac{1}{r} \frac{d f}{d r}-\frac{4 f}{r^{2}}\right)=0\]

Esto tiene la solución general

\[f(r) = Ar^2 + Br^4 + C \dfrac{1}{r^2} + D\]

La función de tensión obtenida de las Eqns. 5.1.17 y 5.1.18 se utiliza ahora para escribir expresiones para las tensiones de acuerdo con la Ecuación 5.1.14, y las constantes determinadas usando las condiciones de límite en Eqns. 5.1.15 y 5.1.16; esto da

\[A=-\frac{\sigma}{4}, \quad B=0, \quad C=-\frac{a^{4} \sigma}{4}, \quad D=\frac{a^{2} \sigma}{2}\]

Sustituyendo estos valores en las expresiones para estrés y reemplazando el\(\sigma /2\) que se eliminó temporalmente, las expresiones finales para las tensiones son

\[\begin{array} {rcl} {\sigma_r} & = & {\dfrac{\sigma}{2} (1 - \dfrac{a^2}{r^2}) + \dfrac{\sigma}{2} (1 + \dfrac{3a^4}{r^4} - \dfrac{4a^2}{r^2}) \cos 2 \theta} \\ {\sigma_{\theta}} & = & {\dfrac{\sigma}{2} (1 + \dfrac{a^2}{r^2}) - \dfrac{\sigma}{2} (1 + \dfrac{3a^4}{r^4}) \cos 2 \theta} \\ {\tau_{r \theta}} & = & {-\dfrac{\sigma}{2} (1 - \dfrac{3a^4}{r^4} + \dfrac{2a^2}{r^2}) \sin 2 \theta} \end{array}\]

Como se ve en la gráfica de la Figura\(\PageIndex{1}\), la tensión alcanza un valor máximo de\((\sigma_{\theta})_{\max} = 3\sigma\) en la periferia del agujero (\(r = a\)), en una posición diametral transversal a la dirección de carga (\(\theta = \pi /2\)). El factor de concentración de estrés, o SCF, para este problema es por lo tanto de 3. La tensión\(x\) -dirección cae a cero en la posición\(\theta = \pi /2\)\(r = a\), ya que debe satisfacer la condición de límite libre de tensión en la periferia del agujero.

Figura\(\PageIndex{3}\): Tensiones cerca del agujero circular. (a) Contornos de\(\sigma_y\) (tensión de campo lejano aplicada en\(y\) dirección). b) Variación de\(\sigma_y\) y\(\sigma_x\) a lo largo de\(\theta = \pi /2\) la línea.

Tenga en cuenta que en el caso de un agujero circular el SCF no depende del tamaño del orificio: cualquier agujero, por pequeño que sea, aumenta las tensiones locales cerca del orificio en un factor de tres. Esta es una consideración muy seria en el diseño de estructuras que deben ser perforadas y remachadas en montaje. Este es el caso en la construcción de la mayoría de los fuselajes de avión, cuya piel debe soportar tensiones sustanciales ya que la presión diferencial de la cabina es ciclada aproximadamente 10 psig durante cada vuelo. La región de alta tensión cerca de los agujeros del remache tiene una propensión peligrosa a incubar grietas por fatiga, y se han rastreado varias fallas catastróficas de aeronaves exactamente a esta causa.

Tenga en cuenta también que el efecto de concentración de esfuerzos se limita a la región bastante cercana al agujero, con las tensiones que caen a sus valores de campo lejano dentro de tres diámetros de orificio o así. Esta es una manifestación del principio de San Venant (El científico francés Barr ́e de Saint-Venant (1797—1886) es uno de los grandes pioneros en mecánica de materiales.), que es una afirmación de sentido común de que la influencia de una perturbación en el campo del estrés se limita en gran medida a la región de la perturbación. Este principio es extremadamente útil en aproximaciones de ingeniería, pero por supuesto se debe tener en cuenta la concentración de esfuerzos cerca de la propia perturbación.

Cuando al inicio de esta sección tomamos el tamaño de la placa para ser “infinito en extensión lateral”, realmente nos referimos a que las condiciones de tensión en los bordes de la placa estaban lo suficientemente alejadas del agujero como para que no influyeran en el estado de tensión cerca del agujero. Con la solución Kirsch ahora en la mano, podemos ser más realistas al respecto: la placa debe ser tres veces más grande que el agujero, o la solución de Kirsch no será confiable.

Funciones complejas

En muchos problemas de interés práctico, es conveniente utilizar las funciones de estrés como funciones complejas de dos variables. Veremos que éstas tienen la capacidad de satisfacer las ecuaciones gobernantes automáticamente, dejando solo los ajustes necesarios para que coincidan con las condiciones de contorno. Por esta razón, los métodos complejo-variables juegan un papel importante en el análisis teórico de estrés, e incluso en este tratamiento introductorio deseamos ilustrar el poder del método. Para delinear algunas relaciones necesarias, considere\(z\) ser un número complejo en coordenadas\(x\) cartesianas\(y\) y/o coordenadas polares\(r\) y\(\theta\) como

\[z = x + iy = r^{i \theta}\]

donde\(i = \sqrt{-1}\). Una función analítica\(f(z)\) es aquella cuyas derivadas dependen\(z\) solamente, y toma la forma

\[f(z) = \alpha + i \beta\]

donde\(\alpha\) y\(\beta\) son funciones reales de\(x\) y\(y\). Se demuestra fácilmente que\(\alpha\) y\(\beta\) satisfacer las ecuaciones de Cauchy-Riemann:

\[\dfrac{\partial \alpha}{\partial x} = \dfrac{\partial \beta}{\partial y}\ \ \ \ \ \dfrac{\partial \alpha}{\partial y} = -\dfrac{\partial \beta}{\partial x}\]

Si el primero de ellos se diferencia con respecto\(x\) y el segundo con respecto a\(y\), y los resultados agregados, obtenemos

\[\dfrac{\partial^2 \alpha}{\partial x^2} + \dfrac{\partial^2 \alpha}{\partial y^2} \equiv \nabla^2 \alpha = 0\]

Esta es la ecuación de Laplace, y cualquier función que satisfaga esta ecuación se denomina función armónica. Equivalentemente,\(\alpha\) podría haber sido eliminado a favor de\(\beta\) dar\(\nabla^2 \beta = 0\), por lo que tanto la parte real como la imaginaria de cualquier función compleja brindan soluciones a la ecuación de Laplace. Consideremos ahora una función de la forma\(x \psi\), donde\(\psi\) es armónica; se puede demostrar por diferenciación directa que

\[\nabla^4 (x \psi) = 0\]

es decir, cualquier función de la forma\(x\psi\), donde\(\psi\) es armónica, satisface la Ecuación 5.1.12, y muchas así se utilizarán como una función de tensión. De igual manera, se puede demostrar que\(y \psi\) y también\((x^2 + y^2) \psi = r^2 \psi\) son adecuados, como es\(\psi\) en sí mismo. En general, se puede obtener una función de tensión adecuada a partir de dos funciones analíticas cualesquiera\(\psi\) y de\(\chi\) acuerdo con

\[\phi = \text{Re} [(x - iy) \psi (z) + \chi (z)]\]

donde "\(\text{Re}\)" indica la parte real de la expresión compleja. Las tensiones correspondientes a esta función\(\phi\) se obtienen como

\[\begin{array} {rcl} {\sigma_x + \sigma_y} & = & {4 \text{Re} \psi' (z)} \\ {\sigma_y - \sigma_x + 2 i \tau_{xy}} & = & {2 [\bar{z} \psi '' (z) + \chi '' (z)]} \end{array}\]

donde los primos indican diferenciación con respecto a\(z\) y la barra superior indica la función conjugada obtenida reemplazando\(i\) con\(-i\); por lo tanto\(\bar{z} = x - iy\).

Tensiones alrededor de un agujero elíptico

En un desarrollo muy importante para la teoría de la fractura, Inglis (C.E. Inglis, “Tenses in a Plate Due to the Presence of Cracks and Sharp Corners”, Transactions of the Institution of Naval Architects, Vol. 55, Londres, 1913, pp. 219—230.) utilizó funciones potenciales complejas para extender el trabajo de Kirsch para tratar el campo de tensión alrededor de una placa que contiene un agujero elíptico en lugar de circular. Esto permite que las geometrías similares a grietas sean tratadas haciendo que el eje menor de la elipse sea pequeño. Es conveniente trabajar en\(\alpha, \beta\) coordenadas elípticas, como se muestra en la Figura 4, definidas como

\[x = c \cosh \alpha \cos \beta, y = c \sin h \alpha \sin \beta\]

Figura 4: Coordenadas elípticas.

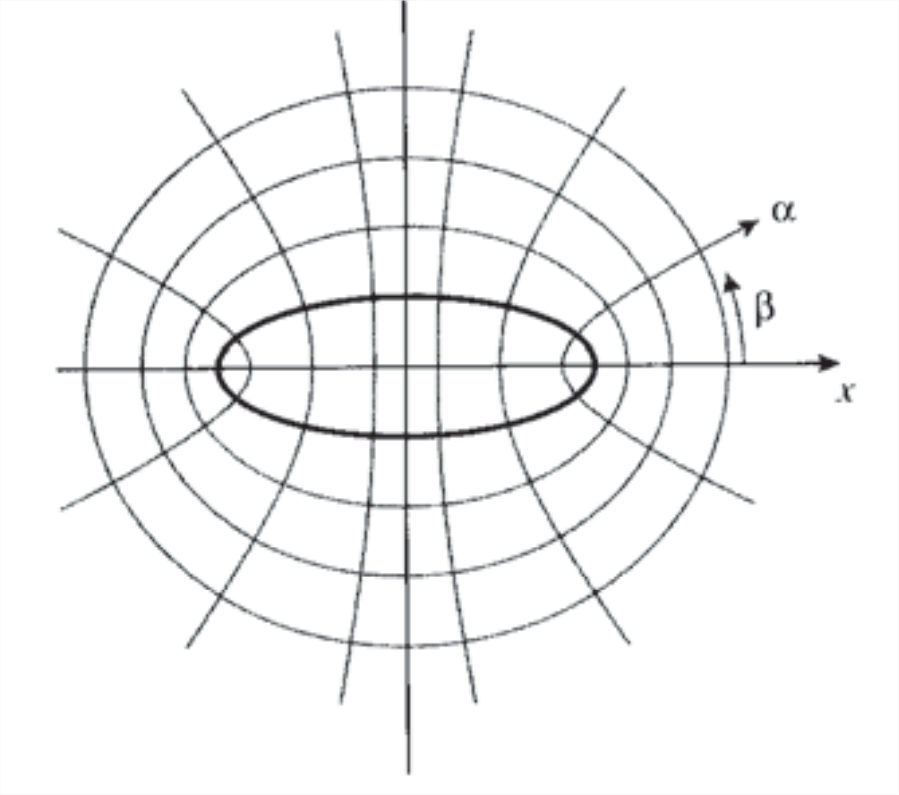
donde\(c\) es una constante. Si\(\beta\) se elimina esto se ve a su vez como equivalente a

\[\dfrac{x^2}{\cosh^2 \alpha} + \dfrac{y^2}{\sinh^2 \alpha} = c^2\]

En el límite de la elipse\(\alpha = \alpha_0\), así podemos escribir

\[c \cosh \alpha_0 = a, c \sinh \alpha_0 = b\]

donde\(a\) y\(b\) son constantes. En el límite, entonces

\[\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\]

que se reconoce como la ecuación cartesiana de una elipse, con\(a\) y\(b\) siendo los radios mayor y menor. Las coordenadas elípticas se pueden escribir en términos de variables complejas como

\[z = c \cosh \zeta, \ \ \ \ \zeta = \alpha + i \beta\]

A medida que se recorre el límite de la elipse,\(\alpha\) permanece constante\(\alpha_0\) mientras\(\beta\) varía de 0 a\(2\pi\). De ahí que las tensiones deben ser periódicas en\(\beta\) con periodo\(2\pi\), al tiempo que se vuelven iguales a la tensión uniaxial de campo lejano\(\sigma_y = \sigma, \sigma_x = \tau_{xy} = 0\) lejos de la elipse; la Ecuación 5.1.26 da entonces

\[\left \{ \begin{array} {rcl} {4 \text{Re} \psi ' (z)} & = & {\sigma} \\ {2[\bar{z} \psi '' (z) + \chi '' (z)]} & = & {\sigma} \end{array} \right \} \zeta \to \infty\]

Estas condiciones límite pueden ser satisfechas por funciones potenciales en las formas

\(\begin{array} {rcl} {4 \psi (z)} & = & {Ac \cosh \zeta + Bc \sinh \zeta} \\ {4 \chi (z)} & = & {Cc^2 \zeta + Dc^2 \cosh 2 \zeta + Ec^2 \sinh 2 \zeta} \end{array}\)

donde\(A,B,C,D,E\) hay constantes a determinar a partir de las condiciones de contorno. Cuando esto se hace, los potenciales complejos se dan como

\[4 \psi(z)=\sigma c\left[\left(1+e^{2 \alpha_{0}}\right) \sinh \zeta-e^{2 \alpha_{0}} \cosh \zeta\right]\]

\[4 \chi(z)=-\sigma c^{2}\left[\left(\cosh 2 \alpha_{0}-\cosh \pi\right) \zeta+\frac{1}{2} e^{2 \alpha_{0}}-\cosh 2\left(\zeta-\alpha_{0}-i \frac{\pi}{2}\right)\right]\]

Las tensiones\(\sigma_x, \sigma_y\), y se\(\tau_{xy}\) pueden obtener mediante el uso de estas en Eqns. 5.1.26. Sin embargo, la cantidad de trabajo en la realización de estas sustituciones no debe estornudarse, y antes de que las computadoras estuvieran generalmente disponibles, la solución Inglis era de un uso algo limitado para sondear la naturaleza del campo de estrés cerca de las puntas de las grietas.

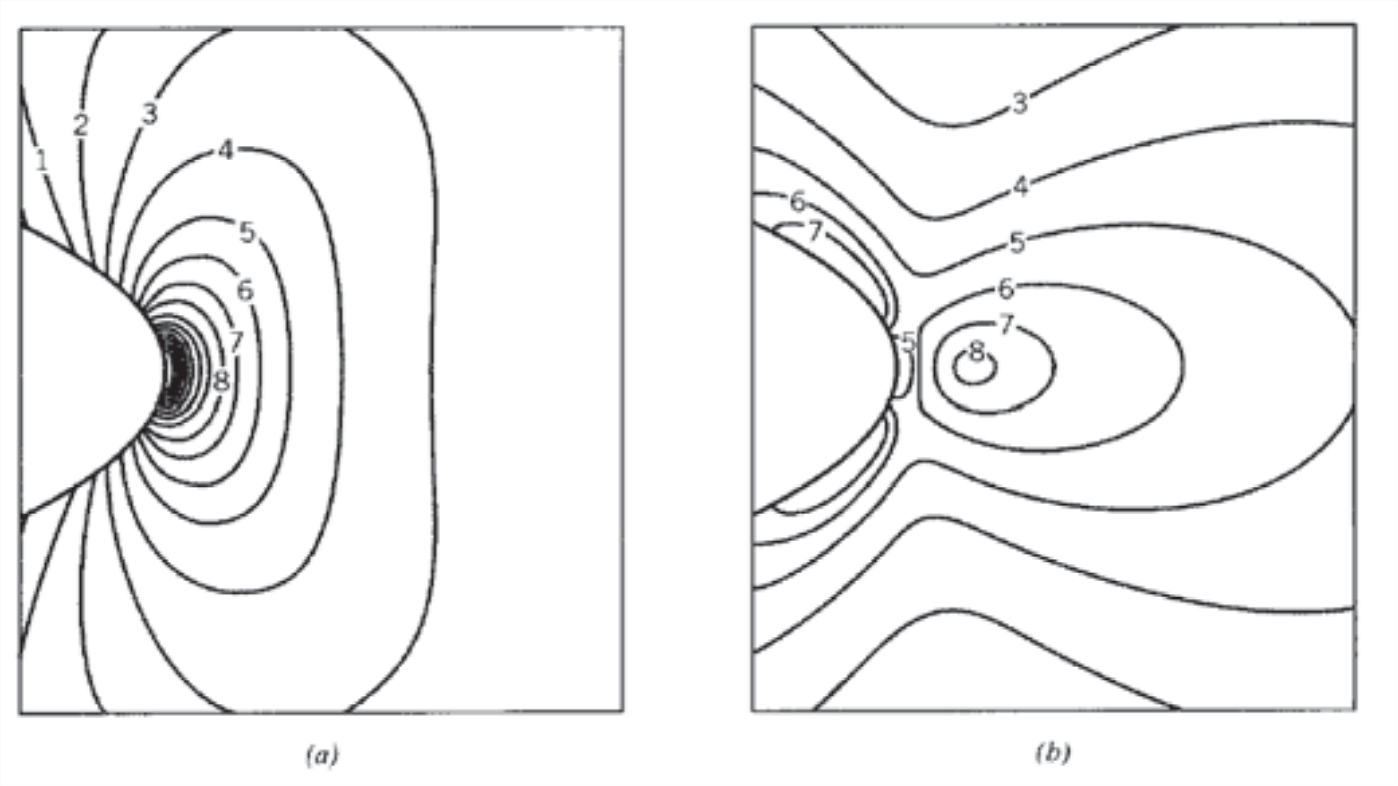
Figura 5: Campo de tensión en las proximidades de un orificio elíptico, con esfuerzo uniaxial aplicado en\(y\) dirección. (a) Contornos de\(\sigma_y\), (b) Contornos de\(\sigma_x\).

La Figura 5 muestra los contornos de estrés calculados por Cook y Gordon (J.E. Gordon, The Science of Structures and Materials, Scientific American Library, Nueva York, 1988.) a partir de las ecuaciones de Inglis. Una fuerte concentración de tensión de la tensión\(\sigma_y\) se observa en la periferia del agujero, como sería de esperar. La tensión horizontal\(\sigma_x\) va a cero en esta misma posición, ya que debe satisfacer allí las condiciones límite. Tenga en cuenta sin embargo que\(\sigma_x\) exhibe una concentración de estrés leve (una quinta parte de eso para\(\sigma_y\), resulta) a poca distancia del agujero. Si el material tiene planos de debilidad a lo largo de la\(y\) dirección, por ejemplo como entre las fibrillas de la madera o muchas otras estructuras biológicas, el estrés\(\sigma_x\) podría provocar que una división se abra en la\(y\) dirección justo por delante de la grieta principal. Esto actuaría para despuntar y detener la grieta, y así impartir una medida de tenacidad al material. Este efecto a veces se llama el mecanismo de endurecedor Cook-Gordon.

Las matemáticas de la solución Inglis son más simples en la superficie del agujero elíptico, ya que aquí el componente normal\(\sigma_{\alpha}\) debe desaparecer. El componente de tensión tangencial se puede calcular directamente:

\[\left(\sigma_{\beta}\right)_{\alpha=\alpha_{0}}=\sigma e^{2 \alpha_{0}}\left[\frac{\sinh 2 \alpha_{0}\left(1+e^{-2 \alpha_{0}}\right)}{\cosh 2 \alpha_{0}-\cos 2 \beta}-1\right]\]

El mayor estrés ocurre al final del eje mayor\((\cos 2 \beta = 1)\):

\[(\sigma_{\beta})_{\beta = 0, \pi} = \sigma_y = \sigma (1 + 2 \dfrac{a}{b})\]

Esto también se puede escribir en términos del radio de curvatura\(\rho\) en la punta del eje mayor como

\[\sigma_y = \sigma (1 + 2 \sqrt{\dfrac{a}{\rho}})\]

Este resultado es inmediatamente útil: es evidente que las grietas grandes son peores que las pequeñas (la tensión local aumenta con el tamaño de la grieta\(a\)), y también es obvio que los huecos agudos (decrecientes\(\rho\)) son peores que los redondeados. Tenga en cuenta también que la tensión\(\sigma_y\) aumenta sin límite a medida que la grieta se vuelve más afilada (\(\rho \to 0\)), por lo que el concepto de un factor de concentración de tensión se vuelve difícil de usar para grietas muy afiladas. Cuando los ejes mayor y menor de la elipse son los mismos (\(b = a\)), el resultado se vuelve idéntico al del agujero circular esbozado anteriormente.

Tensiones cerca de una grieta afilada

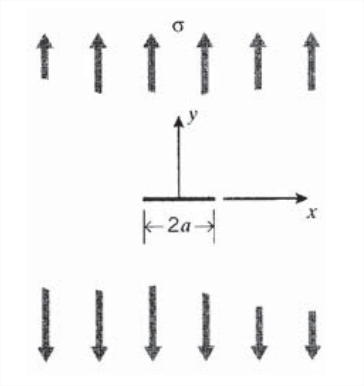
Figura 6: Grieta afilada en una lámina infinita.

La solución Inglis es difícil de aplicar, sobre todo a medida que la grieta se agudiza. Un enfoque más manejable y ahora más ampliamente utilizado fue desarrollado por Westergaard (Westergaard, H.M., “Bearing Pressions and Cracks”, Transactions, Am. Soc. Mech. Engrs., Journal of Applied Mechanics, Vol. 5, p. 49, 1939.), que trata una grieta aguda de longitud\(2a\) en una lámina delgada pero infinitamente ancha (ver Figura 6). Las tensiones que actúan perpendicularmente a las superficies libres de grietas (los “flancos” de la grieta) deben ser cero, mientras que a distancias alejadas de la grieta deben acercarse a las tensiones impuestas por el campo lejano. Considerar una función armónica\(\phi (z)\), con primera y segunda derivadas\(\phi '(z)\) y\(\phi '' (z)\), y primera y segunda integrales\(\bar{\phi} (z)\) y\(\bar{\bar{\phi}}(z)\). Westergaard construyó una función de estrés como

\[\Phi = \text{Re} \bar{\bar{\phi}} (z) + y \text{Im} \bar{\phi} (z)\]

Se puede demostrar directamente que las tensiones derivadas de esta función satisfacen el equilibrio, la compatibilidad y las relaciones constitutivas. La función\(\phi (z)\) necesaria aquí es una función armónica tal que las tensiones se acerquen al valor de campo lejano de\(\sigma\) al infinito, pero sean cero en los flancos de la grieta excepto en la punta de la grieta donde la tensión queda ilimitada:

\(\sigma_y = \begin{cases} \sigma, x \to \pm \infty, -a < x < + a,y = 0 \\ \infty, x = \pm \infty \end{cases}\)

Estas condiciones son satisfechas por funciones complejas de la forma

\[\phi (z) = \dfrac{\sigma}{\sqrt{1 - a^2/z^2}}\]

Esto da la singularidad necesaria para\(z = \pm a\), y las otras condiciones de contorno también se pueden verificar directamente. Las tensiones se encuentran ahora por diferenciaciones adecuadas de la función de estrés; por ejemplo

\(\sigma_y = \dfrac{\partial^2 \Phi}{\partial x^2} = \text{Re} \phi (z) + y \text{Im} \phi ' (z)\)

En cuanto a la distancia\(r\) desde la punta de la grieta, esto se convierte en

\[\sigma_y = \sigma \sqrt{\dfrac{a}{2r}} \cdot \cos \dfrac{\theta}{2} (1 + \sin \dfrac{\theta}{2} \sin \dfrac{3\theta}{2}) + \cdots\]

donde estos son los términos iniciales de una aproximación en serie. Cerca de la punta de la grieta\(r \ll a\), cuando, podemos escribir

\[(\sigma_y)_{y = 0} = \sigma \sqrt{\dfrac{a}{2r}} \equiv \dfrac{K}{\sqrt{2 \pi r}}\]

donde\(K = \sigma \sqrt{\pi a}\) está el factor de intensidad de estrés, con unidades de\(Nm^{-3/2}\) o\(\text{psi} \sqrt{\text{in}}\). (El factor\(\pi\) parece redundante aquí ya que aparece con la misma potencia tanto en el numerador como en el denominador, pero generalmente se incluye como se escribe aquí para concordancia con la literatura más antigua). Veremos en el Módulo sobre Fractura que el factor de intensidad de tensión es una medida comúnmente utilizada de la fuerza impulsora para la propagación de grietas, y por lo tanto subyace a gran parte de la mecánica moderna de fracturas. La dependencia del estrés a la distancia de la grieta es singular, con una\(1/\sqrt{r}\) dependencia. El factor K escala la intensidad de la distribución general de tensiones, con la tensión siempre quedando sin límites a medida que se aproxima la punta de la grieta.

Ejercicio\(\PageIndex{1}\)

Expandir las ecuaciones gobernantes (Eqns. 5.1.1 - 5.1.3) en dos dimensiones cartesianas. Identificar las funciones desconocidas. ¿Cuántas ecuaciones e incógnitas hay?

Ejercicio\(\PageIndex{2}\)

Considere un recipiente a presión de pared gruesa de radio interior\(r_i\) y radio exterior\(r_o\), sometido a una presión interna\(p_i\) y una presión externa\(p_o\).

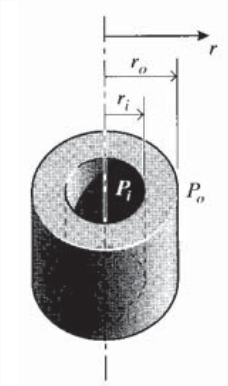
Asumir una solución de prueba para el desplazamiento radial de la forma\(u(r) = Ar + B/r\); esta relación puede mostrarse para satisfacer las ecuaciones gobernantes para las ecuaciones de equilibrio, deformación-desplazamiento y tensión-deformación.

a) Evaluar las constantes\(A\) y\(B\) usar las condiciones de contorno

\[\sigma_r = -p_i @ r = r_i, \sigma_r = -p_0 @ r = r_o\]

b) Luego demuestre que

\[\sigma_{r}(r)=-\frac{p_{i}\left[\left(r_{o} / r\right)^{2}-1\right]+p_{o}\left[\left(r_{o} / r_{i}\right)^{2}-\left(r_{o} / r\right)^{2}\right]}{\left(r_{o} / r_{i}\right)^{2}-1}\]

Ejercicio\(\PageIndex{3}\)

Justificar las condiciones de contorno dadas en Eqns. 5.1.14 para la tensión en coordenadas circulares (\(\sigma_r, \sigma_{\theta}, \tau_{xy}\)) apropiadas a una placa cargada uniaxialmente que contiene un agujero circular.

Ejercicio\(\PageIndex{4}\)

Mostrar que la función Airy\(\phi (x, y)\) definida por Eqns. 5.1.11 satisface las ecuaciones de equilibrio.

Ejercicio\(\PageIndex{5}\)

Mostrar que la tensión funciona en forma de polinomios cuadráticos o cúbicos\((\phi = a_2 x^2 + b_2 xy + c_2 y^2\) y\(\phi = a_3 x^3 + b_3 x^2 y + c_3 xy^2 + d_3 y^3\)) automáticamente satisfacer la relación gobernante\(\nabla^4 \phi = 0\).

Ejercicio\(\PageIndex{6}\)

Escribir las tensiones\(\sigma_x, \sigma_y, \tau_{xy}\) correspondientes a las funciones de esfuerzo cuadrático y cúbico del problema anterior.

Ejercicio\(\PageIndex{7}\)

Elija las constantes en la función de esfuerzo cuadrático de los dos problemas anteriores para representar (a) tensión simple, (b) tensión biaxial y (c) cizallamiento puro de una placa rectangular.

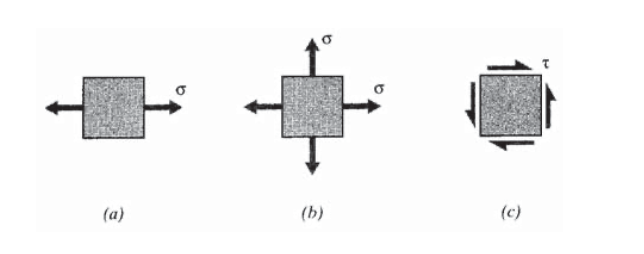
Ejercicio\(\PageIndex{8}\)

Elija las constantes en la función de esfuerzo cúbico de los problemas anteriores para representar la flexión pura inducida por parejas aplicadas a lados verticales de una placa rectangular.

Ejercicio\(\PageIndex{9}\)

Considera una viga en voladizo de sección transversal rectangular y anchura\(b = 1\), cargada en el extremo libre (\(x = 0\)) con una fuerza\(P\). En el extremo libre, se pueden escribir las condiciones de límite sobre la tensión\(\sigma_x = \sigma_y = 0\), y

\(\int_{-h/2}^{h/2} \tau_{xy} \ dy = P\)

Los bordes horizontales no están cargados, así que también tenemos eso\(\tau_{xy} = 0\) en\(y = \pm h/2\).

a) Demostrar que estas condiciones son satisfechas por una función de estrés de la forma

\(\phi = b_2 xy + d_4 xy^3\)

b) Evaluar las constantes para demostrar que las tensiones pueden escribirse

\[\sigma_{x}=\frac{P x y}{I}, \quad \sigma_{y}=0, \quad \tau_{x y}=\frac{P}{2 I}\left[\left(\frac{h}{2}\right)^{2}-y^{2}\right]\]

de acuerdo con la teoría elemental de flexión de vigas (Módulo 13).