5.2: Soluciones Experimentales
- Page ID
- 83319
Introducción
Como se vio en módulos anteriores, el análisis de tensiones incluso de geometrías de apariencia simple puede conducir a complicadas maniobras matemáticas. Los artículos reales —cigüeñales de motor, prótesis médicas, raquetas de tenis, etc.— tienen formas de límites que no se pueden describir matemáticamente fácilmente, y aunque lo fueran sería extremadamente difícil adaptarles soluciones de las ecuaciones gobernantes. Una aproximación a este punto muerto es la experimental, en la que se busca construir un modelo de laboratorio físico que de alguna manera revele las tensiones de una manera medible.
Es la naturaleza de las fuerzas y tensiones que no pueden medirse directamente. Es el efecto de una fuerza que es medible: cuando pesamos un objeto en una escala de resorte, en realidad estamos midiendo el estiramiento del resorte, y luego calculando la fuerza a partir de la ley de Hooke. El análisis de estrés experimental, entonces, es en realidad un análisis de deformación experimental. La dificultad es que las tensiones en el régimen elástico lineal son casi siempre pequeñas, del orden del 1% o menos, y el arte en este campo es el de detectar e interpretar pequeños desplazamientos. Buscamos fenómenos que exhiban cambios grandes y medibles debido a desplazamientos pequeños y difíciles de medir. Hay una serie de tales técnicas, y tres de ellas se esbozarán brevemente y en las secciones a seguir. Se ha desarrollado una buena metodología en torno a estos y otros métodos experimentales, y se requeriría tanto una lectura adicional (Manual sobre Análisis Experimental de Estrés, Tercera Edición, Society of Experimental Stress Analysis (ahora Society of Experimental Mechanics), 1978.) como práctica de laboratorio para poner convertirse en competentes en esta área.
Medidores de tensión
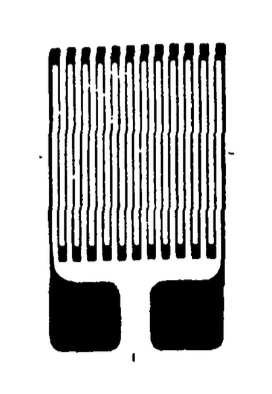
El término “galga extensiométrica” generalmente se refiere a un alambre delgado o lámina, plegado hacia adelante y hacia atrás sobre sí mismo y unido a la superficie del espécimen como se ve en la Figura 1, que es capaz de generar una medida eléctrica de tensión en el espécimen. A medida que el alambre se estira junto con el espécimen, la resistencia eléctrica del cable\(R\) cambia tanto porque aumenta su longitud\(L\) como su área de sección transversal\(A\) se reduce. Para muchas resistencias, estas variables están relacionadas por la simple expresión descubierta en 1856 por Lord Kelvin:
\(R = \dfrac{\rho L}{A}\)
donde aquí\(\rho\) está la resistividad del material. Para expresar el efecto de una deformación\(\epsilon = dL/L\) en la dirección larga del cable sobre la resistencia eléctrica, asuma un cable circular con\(A = \pi r^2\) y tome logaritmos:
El diferencial total de esta expresión da
Desde
\(\epsilon_r = \dfrac{dr}{r} = -v \dfrac{dL}{L}\)
entonces
\(\dfrac{dR}{R} = \dfrac{d \rho}{\rho} (1 + 2v) \dfrac{dL}{L}\)
P.W. Bridgeman (1882 - 1961) en 1929 estudió el efecto del cambio de volumen sobre la resistencia eléctrica y encontró que éstas variaban proporcionalmente:
\[\dfrac{d\rho}{\rho} = \alpha_R \dfrac{dV}{V}\]
donde\(\alpha_R\) es la constante de proporcionalidad entre el cambio de resistencia y el cambio de volumen. Escribiendo el cambio de volumen en términos de cambios en longitud y área, esto se convierte en
De ahí
\[\dfrac{dR/R}{\epsilon} = (1 + 2v) + \alpha_R (1 - 2v)\]
Esta cantidad se llama factor de calibre, GF. Constantan, una aleación 45/55 níquel/cobre, tiene\(\alpha_R = 1.13\) y\(v = 0.3\), dando\(GF \approx 2.0\). Este material también tiene un coeficiente de resistividad de baja temperatura, lo que reduce la sensibilidad a la temperatura de la galga extensiométrica.
Figura 2: Circuito de puente de Wheatstone para galgas extensométricas.
Un cambio en la resistencia de solo 2%, que sería generado por un medidor con\(GF = 2\) un 1% de deformación, no se notaría en un ohmímetro simple. Por esta razón, las galgas extensométricas casi siempre están conectadas a un circuito Wheatstone Bridge como se ve en la Figura 2. El circuito se puede ajustar por medio de la resistencia variable\(R_2\) para producir un voltaje de salida cero\(V_{out}\) antes de aplicar tensión al medidor. Típicamente, la resistencia del medidor es aproximadamente 350\(\Omega\) y el voltaje de excitación está cerca\(10V\). Cuando la resistencia del medidor se cambia por deformación, el puente está desequilibrado y aparece un voltaje en la salida de acuerdo con la relación
\(\dfrac{V_{out}}{V_{in}} = \dfrac{\Delta R}{2R_0}\)
donde\(R_0\) está la resistencia nominal de los cuatro elementos del puente. El voltaje de salida se mide fácilmente porque es una desviación de cero en lugar de ser un cambio relativamente pequeño superpuesto a una cantidad mucho mayor; por lo tanto, puede amplificarse para adaptarse a las necesidades del sistema de adquisición de datos.
La compensación de temperatura se puede lograr haciendo un elemento de puente en el lado opuesto del puente del medidor activo, por ejemplo\(R_3\), un medidor inactivo que se coloca cerca del medidor activo pero no unido a la muestra. Los cambios de resistencia en el medidor activo debido a la temperatura serán entonces compensados, siendo un cambio de resistencia igual en el otro brazo del puente.
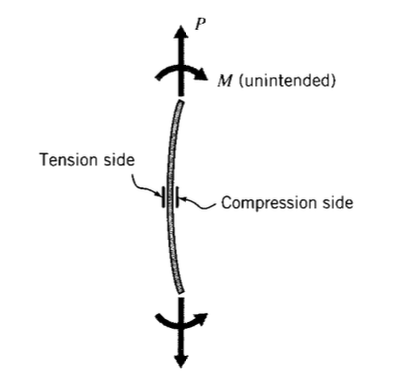
A menudo es difícil montar una muestra de tracción en la máquina de ensayo sin aplicar inadvertidamente flexión además de cargas de tracción. Si se aplicara un solo calibre al lado convexo exterior del espécimen, su lectura sería erróneamente alta. De manera similar, un medidor colocado en el lado cóncavo-hacia adentro o de compresión leería baja. Estos errores de flexión se pueden eliminar mediante el uso de un medidor activo en cada lado de la muestra como se muestra en la Figura 3 y cableándolos en el mismo lado del puente de Wheatstone, por ejemplo\(R_1\) y\(R_4\). El componente de tracción de flexión en un lado de la muestra va acompañado de un componente igual pero compresivo en el otro lado, y estos generarán cambios de resistencia iguales pero opuestos en\(R_1\) y\(R_4\). Por lo tanto, el efecto de la flexión se cancelará, y la combinación de galgas medirá solo la deformación por tracción (con doble sensibilidad, ya que ambos\(R_1\) y\(R_4\) están activos).
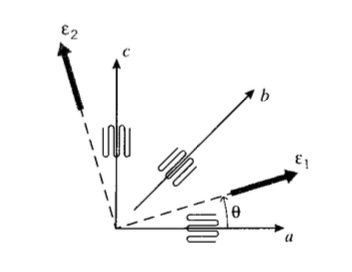
La deformación en la dirección de la galga se puede encontrar directamente a partir del factor de medición (Ecuación 5.2.1). Cuando se desconoce la dirección de la tensión principal, las rosetas de galga extensiométrica son útiles; éstas emplean múltiples calibres en el mismo respaldo de película, orientadas en diferentes direcciones. La roseta rectangular de tres galgas que se muestra en la Figura 4 utiliza dos calibres orientados perpendicularmente, y un tercer calibre orientado en 45\(^{\circ}\) a los dos primeros.
Ejemplo\(\PageIndex{1}\)
Una roseta de tres calibres da lecturas\(\epsilon_0 = 150\mu\)\(\epsilon_{45} = 200 \mu\),, y\(\epsilon_{90} = -100 \mu\) (aquí el\(\mu\) símbolo indica micrómetros por metro). Si alineamos el\(\epsilon_y\) eje\(\epsilon_x\) y a lo largo de las direcciones de\(^{\circ}\) calibre 0\(^{\circ}\) y 90, entonces\(\epsilon_x\) y se\(\epsilon_y\) miden directamente, ya que estas son\(\epsilon_0\) y\(\epsilon_{90}\) respectivamente. Para determinar la deformación por cizallamiento\(\gamma_{xy}\), usamos la regla para la transformación de deformación para escribir la deformación normal a 45\(^{\circ}\):
\(\epsilon_{45} = 200\mu = \epsilon_{x} \cos^2 45 + \epsilon_y \sin^2 45 + \gamma_{xy} \sin 45 \cos 45\)
Sustituyendo los valores conocidos por\(\epsilon_x\) y\(\epsilon_y\), y resolviendo,
\(\gamma_{xy} = 350 \mu\)
Las cepas principales ahora se pueden encontrar como
El ángulo desde el\(x\) eje -hasta el plano principal es
Las tensiones se pueden encontrar a partir de las deformaciones de las relaciones constitutivas del material; por ejemplo, para el acero con\(E = 205\) GPa y\(ν = .3\) la tensión principal es
Para el caso específico de una roseta 0-45-90, la orientación del eje principal de deformación puede ser dada directamente por (M. Hetenyi, ed., Handbook of Experimental Stress Analysis, Wiley, New York, 1950.)
\[\tan 2 \theta = \dfrac{2 \epsilon_b - \epsilon_a - \epsilon_c}{\epsilon_a - \epsilon_c}\]
y las cepas principales son
\[\epsilon_{1, 2} = \dfrac{\epsilon_a + \epsilon_c}{2} \pm \sqrt{\dfrac{(\epsilon_a - \epsilon_b)^2 + (\epsilon_b - \epsilon_c)^2}{2}}\]
Las soluciones gráficas basadas en los círculos de Mohr también son útiles para reducir los datos de salida del medidor.
Los extensómetros se utilizan muy extensamente, y las estructuras críticas, como los aviones, pueden ser instrumentadas con cientos de medidores durante las pruebas. Cada medidor debe estar unido cuidadosamente a la estructura, y conectado por sus dos cables a la unidad de acondicionamiento de señal que incluye la fuente de voltaje de excitación y el puente de Wheatstone. Obviamente, esto puede ser una tarea importante de instrumentación, con la adquisición y reducción de datos asistida por computadora una necesidad práctica.
Fotoelasticidad
Las galgas extensométricas de resistencia al alambre son probablemente el principal dispositivo utilizado en el análisis de esfuerzos experimentales hoy en día, pero tienen la desventaja de monitorear la deformación solo en una sola ubicación. Los métodos de fotoelasticidad y muaré, que se describen en las siguientes secciones, son más complicados en concepto y aplicación, pero tienen la capacidad de proporcionar pantallas de campo completo de la distribución de la tensión. La visión intuitiva de estas pantallas puede ser tan valiosa que puede ser innecesario convertirlas a valores numéricos, aunque la conversión se puede hacer si se desea.
Figura 5: Propagación de la luz.
La fotoelasticidad emplea una propiedad de muchos polímeros transparentes y vidrios inorgánicos llamada birrefringencia. Para explicar este fenómeno, recordemos la definición de índice de refracción\(n\), que es la relación entre la velocidad de la luz\(v\) en el medio y la del vacío\(c\):
\[n = \dfrac{v}{c}\]
A medida que el haz de luz viaja en el espacio (ver Figura 5), su vector de campo eléctrico\(E\) oscila hacia arriba y hacia abajo a una frecuencia angular\(\omega\) en un plano fijo, denominado plano de polarización del haz. (La longitud de onda de la luz es\(\lambda = 2\pi c/\omega\).) Un material birrefringente es aquel en el que el índice de refracción depende de la orientación del plano de polarización, y la magnitud de la birrefringencia es la diferencia en los índices:
\(\Delta n = n_{\perp} - n_{\parallel}\)
donde\(n_{\perp}\) y\(n_{\parallel}\) son los índices de refracción en los dos planos. Esos dos planos que producen el máximo\(\Delta_n\) son los planos ópticos principales. Como se muestra en la Figura 6, un material birrefringente puede verse de manera simplista como una persiana veneciana que resuelve un vector de campo eléctrico orientado arbitrariamente en dos componentes, uno en cada uno de los dos planos ópticos principales, después de lo cual cada componente transitará el material a una velocidad diferente de acuerdo con Ecuación 5.2.4. Los dos componentes eventualmente saldrán del material, nuevamente viajando a la misma velocidad pero habiendo sido desplazados en fase uno del otro en una cantidad relacionada con la diferencia en los tiempos de tránsito.
Un material fotoelástico es aquel en el que la birrefringencia depende de la tensión aplicada, y muchos de estos materiales pueden describirse a una buena aproximación por la ley de tensión-óptica
\[\Delta_n = C(\lambda) (\sigma_1 - \sigma_2)\]
donde\(C\) está el coeficiente de tensión-óptica, y la cantidad en el segundo paréntesis es la diferencia entre las dos tensiones principales en el plano normal a la dirección de propagación de la luz; esto es solo el doble del esfuerzo cortante máximo en ese plano. El coeficiente de tensión-óptico es generalmente una función de la longitud de onda\(\lambda\).
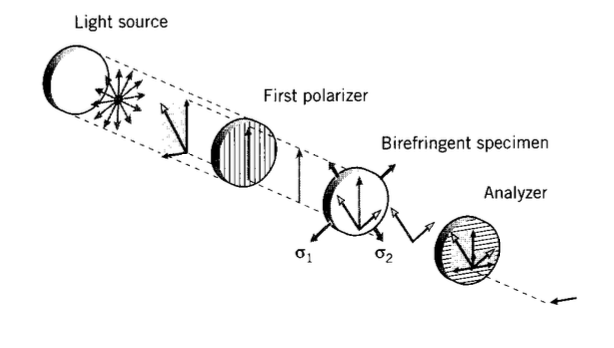
La distribución de esfuerzos en un cuerpo de forma irregular se puede ver replicando la estructura real (probablemente escalada hacia arriba o hacia abajo en tamaño para mayor comodidad) en un material birrefringente como epoxi. Si la estructura se determina estáticamente, las tensiones en el modelo serán las mismas que en la estructura real, a pesar de las diferencias de módulo. Para hacer visible el efecto de birrefringencia, el modelo se coloca entre polarizadores cruzados en un aparato conocido como polariscopio. (Polarizadores como Polaroid, una lámina de polímero que contiene cristales de yoduro orientados, son esencialmente materiales birrefringentes que pasan solo luz polarizada en el plano óptico principal del polarizador).
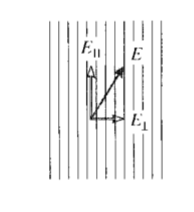
La fuente de radiación puede producir luz blanca convencional (policromática) o filtrada (monocromática). El vector de campo eléctrico de luz que incide en el primer polarizador con una orientación arbitraria puede resolverse en dos componentes como se muestra en la Figura 7, uno en la dirección de polarización y el otro perpendicular a éste. El polarizador bloqueará la componente transversal, permitiendo que la componente paralela pase a través de la muestra. Este componente polarizado se puede escribir
\(u_P = A \cos \omega t\)
donde\(u_P\) está la intensidad de campo en el momento\(t\). El espécimen birrefringente resolverá este componente en dos componentes adicionales, a lo largo de cada una de las direcciones principales de tensión; estos pueden escribirse como
\(u_1 = A \cos \alpha \cos \omega t\)
\(u_2 = A \sin \alpha \cos \omega t\)
donde α es el ángulo (desconocido) que hacen los planos de tensión principales con la dirección de polarización. Ambos nuevos componentes pasan a través del espécimen, pero a diferentes velocidades según lo dado por la Ecuación 5.2.5. Después de recorrer el espécimen una distancia\(h\) con velocidades\(v_1\) y\(v_2\), emergen como
Estos dos componentes luego caen sobre el segundo polarizador, orientado\(^{\circ}\) a 90 al primero y conocido como analizador. Cada uno se resuelve de nuevo en componentes adicionales paralelos y perpendiculares al eje del analizador, y los componentes perpendiculares se bloquean mientras los componentes paralelos pasan a través. El componente transmitido se puede escribir como
\(u_A = -u_1' \sin \alpha + u_2' \cos \alpha\)
Esto es de la forma\(u_A = A' \sin (\omega t - \delta)\), donde\(A'\) es una amplitud y\(\delta\) es un ángulo de fase. Tenga en cuenta que la amplitud es cero, por lo que no se transmitirá ninguna luz, si cualquiera\(\alpha = 0\) o si
\[\dfrac{2 \pi c}{\lambda} ( \dfrac{h}{2v_1} - \dfrac{h}{2v_2} ) = 0, \pi, 2\pi, \cdots\]
El caso para lo cual\(\alpha = 0\) ocurre cuando los planos de tensión principales están alineados con los ejes polarizador-analizador. Todas las posiciones sobre el modelo en el que esto es cierto producen así una extinción de la luz transmitida. Estas se ven como bandas oscuras llamadas isoclínicas, ya que mapean líneas de inclinación constante de los ejes principales de tensión. Estos contornos se pueden fotografiar en una secuencia de orientaciones de polarización, si se desea, para dar una imagen aún más completa de las direcciones de estrés.
Las posiciones de tensión cero también producen extinción, ya que entonces el retardo es cero y los dos componentes ligeros que salen del analizador se cancelan entre sí. El eje neutro de una viga en flexión, por ejemplo, se muestra como una línea negra en el campo observado. A medida que la tensión en una ubicación dada se incrementa desde cero, el desplazamiento de fase creciente entre los dos componentes provoca que la cancelación sea incompleta y se observe luz. Eventualmente, a medida que el estrés se incrementa aún más, el retraso alcanzará\(\delta = \pi\), y la extinción vuelve a ocurrir. Esto produce otra franja oscura en el campo observado. En general, se observan áreas alternas claras y franjas oscuras, correspondientes a órdenes crecientes de extinción.
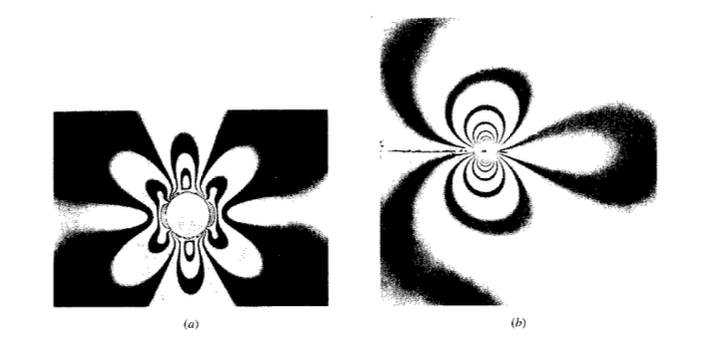
El espaciado de franjas cercanas indica un gradiente de esfuerzo pronunciado, similar a las líneas de elevación en un mapa de contorno geográfico; la Figura 8 muestra los patrones alrededor de los elevadores de tensión circulares y de grietas afiladas. Puede ser suficiente simplemente observar las ubicaciones de alta densidad de flecos para observar la presencia de concentraciones de tensión, que luego podrían eliminarse mediante modificaciones de diseño adecuadas (como redondear esquinas o reubicar discontinuidades geométricas abruptas de regiones de alta tensión). Si se usa luz blanca en lugar de monocromática, se observan líneas de colores brillantes en lugar de franjas oscuras, siendo cada color el complemento de ese color que ha sido llevado a la extinción de acuerdo con la Ecuación 5.2.4. Estas bandas de color constante se denominan isocromáticas.
La conversión de los patrones de franja a valores de estrés numéricos suele ser sencillo pero tedioso, ya que las franjas están relacionadas con la diferencia de estrés\(\sigma_1 - \sigma_2\) en lugar de con una sola tensión. En un límite libre, sin embargo, los componentes de tensión normales al límite deben ser cero, lo que significa que la tensión tangencial al límite es una tensión principal y por lo tanto viene dada directamente por el orden de franja allí. La reducción de patrones fotoelásticos a valores numéricos generalmente implica comenzar en estas superficies libres, y luego trabajar gradualmente en el interior del cuerpo mediante un procedimiento gráfico.
Moire
El término “muaré” se deletrea con una pequeña “m” y deriva no del nombre de alguien sino del nombre de una tela de seda que muestra patrones de bandas claras y oscuras. Bandas de este tipo también se desarrollan por la superposición de dos rejillas casi idénticas, como se podría ver al mirar a través de dos pantallas de ventana ligeramente giradas entre sí. La Figura 9 demuestra que las franjas se desarrollan si las dos rejillas tienen diferentes espacios, así como diferentes orientaciones. Las franjas cambian drásticamente incluso para pequeños movimientos o tensiones en las rejillas, y esta amplificación visual del movimiento se puede utilizar para detectar y cuantificar la tensión en el espécimen.

Como simple ilustración del análisis de deformación de muaré, supongamos que una rejilla de líneas verticales de espaciamiento\(p\) (la rejilla\ espécimen”) está unida al espécimen y que esto se observa mirando a través de otra rejilla\ reference” del mismo período pero no unida al espécimen. Ahora deje que el espécimen sufra una tensión, para que la rejilla del espécimen se estire a un período\(p'\) Aparecerá una franja oscura cuando las líneas de las dos rejillas se superpongan, y esto ocurrirá cuando\(N(p' - p) = p\), ya que después de\(N\) las líneas en la rejilla del espécimen el hueco incremental (\(p' - p\)) se habrá acumulado a una distancia de paso de referencia\(p\). La distancia\(S\) entre las franjas es entonces
\[S = Np' = \dfrac{pp'}{p' - p}\]
La deformación normal\(\epsilon_x\) en la dirección horizontal ahora se da directamente desde el espaciado de las franjas como
\[\epsilon_x = \dfrac{p' - p}{p} = \dfrac{p}{S}\]
También se desarrollarán flecos si la rejilla del espécimen se somete a una rotación relativa a la cuadrícula de referencia: si la rotación es pequeña, entonces
\(\dfrac{p}{S} = \tan \theta \approx \theta\)
\(S = \dfrac{p}{\theta}\)
Este ángulo es también la deformación por cizallamiento\(\gamma_{xy}\), por lo que
\[\gamma_{xy} = \theta = \dfrac{p}{\theta}\]
De manera más general, considere las franjas de interferencia que se desarrollan entre una cuadrícula de referencia vertical y una cuadrícula de espécimen desplazada arbitrariamente (originalmente vertical). La franja de orden cero (\(N = 0\)) es aquella que corresponde a posiciones que tienen desplazamiento horizontal cero, la franja de primer orden (\(N = 1\)) corresponde a movimientos horizontales de exactamente una distancia de paso, etc. El desplazamiento horizontal viene dado directamente por el orden de flecos como\(u = N_p\), a partir del cual el la cepa viene dada por
\[\epsilon_x = \dfrac{\partial u}{\partial x} = p \dfrac{\partial N}{\partial x}\]
por lo que la cepa se da como la pendiente de la franja.
De igual manera, un patrón de muaré desarrollado entre dos rejillas originalmente horizontales, caracterizadas por franjas\(N' = 0, 1, 2, \cdots\) da las deformaciones verticales:
\[\epsilon _y = \dfrac{\partial v}{\partial y} = \dfrac{\partial (N'p)}{\partial y} = p \dfrac{\partial N'}{\partial y}\]
Las deformaciones de cizallamiento se encuentran en las laderas tanto de las franjas\(v\) de campo como de campo:\(u\)
\[\gamma_{xy} = p(\dfrac{\partial N}{\partial y} + \dfrac{\partial N'}{\partial x})\]
La figura 10 muestra las franjas correspondientes a desplazamientos verticales alrededor de un orificio circular en una placa sometida a carga en la\(y\) dirección. La deformación vertical\(\epsilon_y\) es proporcional a la\(y\) distancia entre estas franjas, cada una de las cuales es un contorno de desplazamiento vertical constante. Esta deformación es mayor a lo largo del\(x\) eje -en la periferia del agujero, y menor a lo largo del\(y\) eje -en la periferia del agujero.

Ejercicio\(\PageIndex{1}\)
Una roseta de galga extensiométrica\(0^{\circ}\)\(45^{\circ}\)//de\(90^{\circ}\) tres brazos unida a una muestra de acero da lecturas\(\epsilon_0 = 175 \mu\)\(\epsilon_{45} =150\mu\),, y\(\epsilon_{90} = -120\mu\). Determinar las tensiones principales y la orientación de los planos principales en la ubicación del medidor.
Ejercicio\(\PageIndex{2}\)
Repita el problema anterior, pero con lecturas del medidor\(\epsilon_0 = 150 \mu, \epsilon_{45} = 200 \mu\), y\(\epsilon_{90} = 125 \mu\).


