5.4: Viscoelasticidad Lineal
- Page ID
- 83327
1. Introducción
Este documento pretende delinear un aspecto importante de la respuesta mecánica de polímeros y composites polímero-matriz: el campo de la viscoelasticidad lineal. Los temas que aquí se incluyen tienen como objetivo brindar una introducción instructiva a este amplio y elegante tema, y no deben tomarse como un tratamiento minucioso o integral. Las referencias que aparecen ya sea como notas al pie de página del texto o enumeradas por separado al final de las notas deben ser consultadas para una cobertura más completa.
La respuesta viscoelástica se utiliza a menudo como sonda en la ciencia de polímeros, ya que es sensible a la química y microestructura del material. Los conceptos y técnicas aquí presentados son importantes para este propósito, pero el objetivo principal de este documento es demostrar cómo la viscoelasticidad lineal puede incorporarse a la teoría general de la mecánica de los materiales, de manera que se puedan diseñar estructuras que contengan componentes viscoelásticos y analizadas.
Si bien no todos los polímeros son viscoelásticos en ningún grado práctico importante, e incluso menos son linealmente viscoelásticos (Para una visión general de la teoría viscoelástica no lineal, véase por ejemplo W.N. Findley et al., Creep and Relaxation of Nonlinear Viscoelastic Materials, Dover Publications, Nueva York, 1989.), esta teoría proporciona una aproximación de ingeniería utilizable para muchas aplicaciones en ingeniería de polímeros y compuestos. Incluso en casos que requieren tratamientos más elaborados, la teoría viscoelástica lineal es un punto de partida útil.
2. Mecanismos Moleculares
Cuando se someten a una tensión aplicada, los polímeros pueden deformarse por uno o ambos de dos mecanismos atomísticos fundamentalmente diferentes. Las longitudes y ángulos de los enlaces químicos que conectan los átomos pueden distorsionarse, moviendo los átomos a nuevas posiciones de mayor energía interna. Este es un movimiento pequeño y ocurre muy rápidamente, requiriendo solo\(\approx 10^{-12}\) segundos.
Si el polímero tiene suficiente movilidad molecular, también pueden ser posibles reordenamientos a mayor escala de los átomos. Por ejemplo, la rotación relativamente fácil alrededor de los enlaces simples carbono-carbono del esqueleto puede producir grandes cambios en la conformación de la molécula. Dependiendo de la movilidad, una molécula de polímero puede extenderse en la dirección del estrés aplicado, lo que disminuye su entropía conformacional (la molécula está menos “desordenada”). Los elastómeros —el caucho— responden casi en su totalidad por este mecanismo entrópico, con poca distorsión de sus enlaces covalentes o cambio en su energía interna.
La primera y segunda leyes combinadas de la termodinámica establecen cómo un incremento del trabajo mecánico\(f\ dx\) realizado en el sistema puede producir un aumento en la energía interna\(dU\) o una disminución en la entropía\(dS\):
\[f\ dx = dU - T\ dS\]
Claramente, la importancia relativa de la contribución entrópica aumenta con la temperatura\(T\), y esto proporciona un medio conveniente para determinar experimentalmente si la rigidez del material en origen energético o entrópico. La fuerza de retracción necesaria para sostener una banda de goma en elongación fija aumentará con el aumento de la temperatura, ya que el aumento de la agitación térmica hará que la estructura interna sea más vigorosa en sus intentos naturales de restaurar la aleatoriedad. Pero la fuerza de retracción en una muestra de acero estirada —que muestra poca elasticidad entrópica— disminuirá con la temperatura, ya que la expansión térmica actuará para aliviar la tensión interna.
En contraste con la naturaleza instantánea de la elasticidad controlada energéticamente, los cambios conformacionales o entrópicos son procesos cuyas tasas son sensibles a la movilidad molecular local. Esta movilidad está influenciada por una variedad de factores físicos y químicos, como la arquitectura molecular, la temperatura o la presencia de fluidos absorbidos que pueden hinchar el polímero. A menudo, una simple imagen mental del “volumen libre” —aproximadamente, el espacio disponible para que los segmentos moleculares actúen cooperativamente para llevar a cabo el movimiento o reacción en cuestión— es útil para intuir estas tasas.
Estas tasas de cambio conformacional a menudo se pueden describir con una precisión razonable mediante expresiones de tipo Arrhenius de la forma
\[\text{rate} \propto \exp \dfrac{-E^\dagger}{RT}\]
donde\(E^\dagger\) es una aparente energía de activación del proceso y\(R = 8.314J/mol - ^{\circ}K\) es la Constante de Gas. A temperaturas muy superiores a la “temperatura de transición vítrea”, etiquetada\(T_g\) en la Figura 1, las velocidades son tan rápidas que son esencialmente instantáneas, y el polímero actúa de una manera gomosa en la que exhibe grandes deformaciones instantáneas y totalmente reversibles en respuesta a una tensión aplicada.
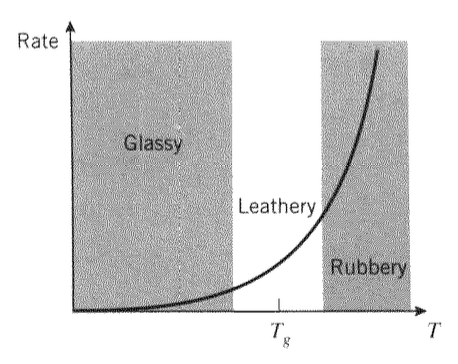
Por el contrario, a temperaturas mucho menores que\(T_g\), las tasas son tan lentas que son insignificantes. Aquí el proceso de desenrollamiento de la cadena está esencialmente “congelado”, por lo que el polímero es capaz de responder solo por estiramiento de enlace. Ahora responde de manera “vidriosa”, respondiendo instantánea y reversiblemente pero siendo incapaz de ser tensa más allá de un pequeño porcentaje antes de fracturarse de manera quebradiza.
En el rango cercano\(T_g\), el material está a medio camino entre los regímenes vítreo y gomoso. Su respuesta es una combinación de fluidez viscosa y solidez elástica, y esta región se denomina “coriácea” o, más técnicamente, “viscoelástica”. El valor de\(T_g\) es un descriptor importante de la respuesta termomecánica del polímero, y es una medida fundamental de la propensión del material a la movilidad. Factores que mejoran la movilidad, como diluyentes absorbidos, estados de estrés expansivo y falta de grupos moleculares voluminosos, todos tienden a producir valores más bajos de\(T_g\). La película transparente de butiral de polivinilo utilizada en los laminados de parabrisas de automóviles es un ejemplo de un material que se usa en el régimen viscoelástico, ya que la respuesta viscoelástica puede ser una fuente de disipación sustancial de energía durante el impacto.
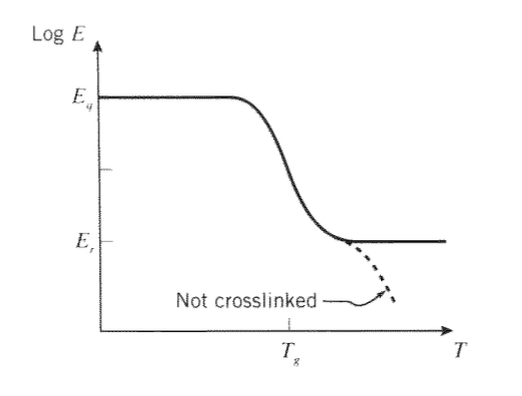
A temperaturas muy por debajo\(T_g\), cuando los movimientos entrópicos se congelan y solo son posibles deformaciones de la unión elástica, los polímeros exhiben un módulo relativamente alto, llamado el “módulo vítreo”\(E_g\), que es del orden de 3 GPa (400 kpsi). A medida que aumenta la temperatura\(T_g\), la rigidez disminuye drásticamente, quizás en dos órdenes de magnitud, a un valor llamado “módulo gomoso”\(E_r\). En elastómeros que han sido reticulados permanentemente por vulcanización al azufre u otros medios, el valor de\(E_r\) está determinado principalmente por la densidad de entrecruzamiento; la teoría cinética de la elasticidad del caucho da la relación como
\[\sigma = NRT (\lambda - \dfrac{1}{\lambda^2})\]
donde\(\sigma\) está la tensión,\(N\) es la densidad de entrecruzamiento (\(mol/m^3\)), y\(\lambda = L/L_0\) es la relación de extensión. La diferenciación de esta expresión da la pendiente de la curva de tensión-deformación en el origen como\(E_r = 3NRT\).
Si el material no está reticulado, la rigidez exhibe una meseta corta debido a la capacidad de los enredos moleculares para actuar como uniones de red; a temperaturas aún más altas los enredos se deslizan y el material se convierte en un líquido viscoso. Ni el módulo vítreo ni el gomoso dependen fuertemente del tiempo, pero en las proximidades de la transición cerca del\(T_g\) tiempo los efectos pueden ser muy importantes. Claramente, una gráfica de módulo versus temperatura, tal como se muestra en la Figura 2, es una herramienta vital en la ciencia e ingeniería de materiales poliméricos. Proporciona un mapa de una propiedad vital de ingeniería, y también es una huella digital de los movimientos moleculares disponibles para el material.
3. Aspectos fenomenológicos
Experimentalmente, se busca caracterizar los materiales mediante la realización de pruebas de laboratorio simples a partir de las cuales se puede obtener información relevante para las condiciones reales de uso. En el caso de materiales vis- coelásticos, la caracterización mecánica a menudo consiste en realizar pruebas de tracción uniaxiales similares a las utilizadas para sólidos elásticos, pero modificadas para permitir la observación de la dependencia temporal de la respuesta del material. Aunque se han utilizado muchos de estos “ensayos de tracción viscoelástica”, uno de los más comunes encuentra solo tres: fluencia, relajación de esfuerzos y carga dinámica (sinusoidal).
Arrastramiento
La prueba de fluencia consiste en medir la deformación dependiente del tiempo\(\epsilon (t) = \delta (t)/L_0\) resultante de la aplicación de una tensión uniaxial constante\(\sigma_0\) como se ilustra en la Figura 3. Estas tres curvas son las cepas medidas a tres niveles de tensión diferentes, cada una dos veces la magnitud de la anterior.
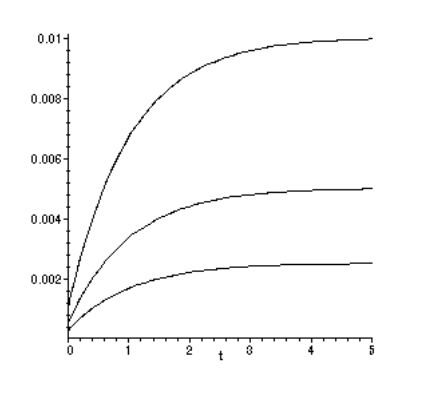
Obsérvese en la Figura 3 que cuando se duplica la tensión, la deformación resultante se duplica en todo su rango de tiempo. Esto ocurre si los materiales son lineales en su respuesta. Si la relación deformación-tensión es lineal, la deformación resultante de una tensión\(a\sigma\), donde\(a\) es una constante, es solo la constante\(a\) multiplicada por la deformación resultante de\(\sigma\) solo. Matemáticamente,
\(\epsilon (a \sigma) = a\epsilon (\sigma)\)
Este es solo un caso de “duplicar la tensión, duplicar la tensión”.
Si las deformaciones de fluencia producidas en un momento dado se grafican como abscisas contra la tensión aplicada como ordenada, se produciría una curva de tensión-deformación “isócrona”. Si el material es lineal, esta “curva” será una línea recta, con una pendiente que aumenta a medida que disminuye el tiempo elegido.
Para materiales lineales, la familia de historias de deformación\(\epsilon (t)\) obtenidas a diversas tensiones constantes puede superponerse normalizándolos en función de la tensión aplicada. La relación de deformación a tensión se denomina “cumplimiento”\(C\), y en el caso de deformación variable en el tiempo que surge de una tensión constante, la relación es la “conformidad de fluencia”:
\(C_{crp} (t) = \dfrac{\epsilon (t)}{\sigma_0}\)
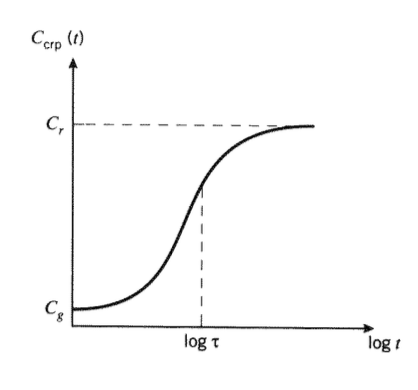
Una forma típica de esta función se muestra en la Figura 4, trazada frente al logaritmo del tiempo. Tenga en cuenta que la forma logarítmica de la gráfica cambia drásticamente la forma de la curva, estirando la porción de corto tiempo de la respuesta y comprimiendo la región de largo tiempo. Al cargarlo, el material se deforma inicialmente al cumplimiento “vítreo”\(C_g\); esta es la deformación elástica correspondiente a la distorsión de la unión. Con el tiempo, el cumplimiento se eleva a un valor de equilibrio o “gomoso”\(C_r\), correspondiente a la extensión gomosa del material. El valor a lo largo de la abscisa etiquetado como\(\log \tau\) "" marca la inflexión de pendiente ascendente a descendente, y\(\tau\) se llama el “tiempo de relajación” del proceso de fluencia.
Relajación del estrés
Otra prueba común, que se realiza fácilmente en Instron u otras máquinas controladas por desplazamiento, consiste en monitorear la tensión dependiente del tiempo resultante de una deformación constante como se ve en la Figura 5. Esto es lo contrario de la Figura 3; aquí las curvas de tensión corresponden a tres niveles diferentes de deformación constante, cada uno dos veces la magnitud del anterior.
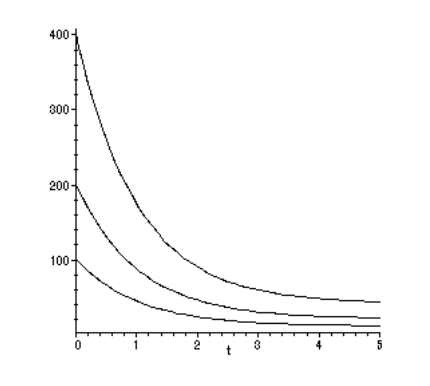
Análogamente con el cumplimiento de fluencia, se pueden superponer las curvas de relajación por medio del “módulo de relajación”, definido como\(E_{rel}(t) = \sigma (t)/\epsilon_0\), representado frente al tiempo logarítmico en la Figura 6. En tiempos cortos, la tensión se encuentra en una meseta alta correspondiente a un módulo “vítreo”\(E_g\), y luego cae exponencialmente a un módulo “gomoso” de equilibrio más bajo a\(E_r\) medida que las moléculas de polímero acomodan gradualmente la deformación por extensión conformacional en lugar de distorsión del enlace.
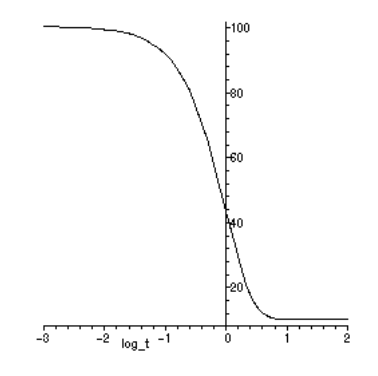
La fluencia y la relajación son manifestaciones de los mismos mecanismos moleculares, y uno debe esperarlo\(E_{rel}\) y\(C_{crp}\) están relacionados. Sin embargo aunque\(E_g = 1/C_g\) y\(E_r = 1/C_r\), en general\(E_{rel} (t) \ne 1/C_{crp} (t)\). En particular, la respuesta de relajación se mueve hacia su valor de equilibrio más rápidamente que la respuesta de fluencia.
Carga dinámica
Las pruebas de fluencia y relajación de esfuerzo son convenientes para estudiar la respuesta del material en tiempos largos (minutos a días), pero menos precisas en tiempos más cortos (segundos y menos). Las pruebas dinámicas, en las que se mide la tensión (o deformación) resultante de una tensión sinusoidal (o tensión), a menudo son adecuadas para completar el rango de respuesta del polímero “a corto plazo”. Cuando un material viscoelástico es sometido a una tensión sinusoidalmente variable, eventualmente se alcanzará un estado estacionario (El tiempo necesario para que el efecto transitorio inicial se agote dependerá en sí mismo del tiempo de respuesta viscoelástico del material, y en algunas situaciones esto puede conducir a errores experimentales. El ejercicio\(\PageIndex{5}\) desarrolla la forma completa de la respuesta dinámica, incluyendo el término transitorio inicial.) en el que la deformación resultante también es sinusoidal, teniendo la misma frecuencia angular pero retardada en fase por un ángulo\(\delta\); esto es análogo a la tensión retardada observada en experimentos de fluencia. La deformación retarda la tensión por el ángulo de fase\(\delta\), y esto es cierto incluso si la deformación en lugar de la tensión es la variable controlada.
Si se selecciona el origen a lo largo del eje de tiempo para que coincida con un tiempo en el que la deformación pasa por su máximo, las funciones de deformación y tensión se pueden escribir como:
\[\epsilon = \epsilon_0 \cos \omega t\]
\[\sigma = \sigma_0 \cos (\omega t + \delta\]
Utilizando una maniobra algebraica común en el análisis de circuitos eléctricos reactivos y otros sistemas armónicos, es conveniente escribir la función de tensión como una cantidad compleja\(\sigma^*\) cuya parte real está en fase con la deformación y cuya parte imaginaria está\(90^{\circ}\) desfasada con ella:
\[\sigma^* = \sigma_0' \cos \omega t + i \sigma_0'' \sin \omega t\]
Aquí\(i = \sqrt{-1}\) y el asterisco denota una cantidad compleja como de costumbre.
Puede ser útil visualizar la tensión y deformación observables como la proyección sobre el eje real de vectores que giran en el plano complejo a una frecuencia\(\omega\). Si capturamos sus posiciones justo cuando el vector de deformación pasa por el eje real, el vector de tensión estará por delante de él por el ángulo de fase\(\delta\) como se ve en la Figura 7.
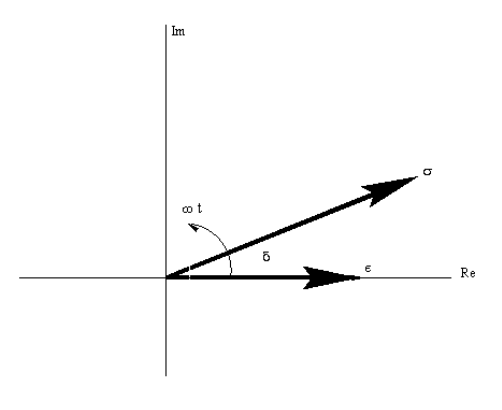
La Figura 7 facilita el desarrollo de las relaciones entre los diversos parámetros en las relaciones armónicas:
\[\tan \delta = \sigma_0''/\sigma_0'\]
\[|\sigma^*| = \sigma_0 = \sqrt{(\sigma_0')^2 + (\sigma_0'')^2}\]
\[\sigma_0' = \sigma_0 \cos \delta\]
\[\sigma_0'' = \sigma_0 \sin \delta\]
Podemos utilizar esta forma compleja de la función de estrés para definir dos módulos dinámicos diferentes, siendo ambos relaciones de tensión a deformación como de costumbre pero teniendo interpretaciones moleculares muy diferentes y consecuencias macroscópicas. El primero de ellos es el módulo “real” o “almacenamiento”, definido como la relación entre la tensión en fase y la deformación:
\[E' = \sigma_0' /\epsilon_0\]
El otro es el módulo “imaginario” o “pérdida”, definido como la relación entre la tensión fuera de fase y la deformación:
\[E'' = \sigma_0''/\epsilon_0\]
Ejemplo\(\PageIndex{1}\)
Los términos “almacenamiento” y “pérdida” se pueden entender más fácilmente considerando el trabajo mecánico realizado por ciclo de carga. La cantidad y\(\int \sigma \ d\epsilon\) es la energía de deformación por unidad de volumen (ya que\ sigma\) = fuerza/área y\(\epsilon\) = distancia/longitud). Integración de los componentes en fase y fuera de fase por separado:
\[W = \oint \sigma d \epsilon = \oint \dfrac{d\epsilon}{dt}dt\]
\[=\int_{0}^{2\pi/\omega} (\sigma_0' \cos \omega t)(-\epsilon_0 \omega \sin \omega t) dt + \int_{0}^{2\pi /\omega} (\sigma_0'' \sin \omega t) (-\epsilon_0 \omega \sin \omega t) dt\]
\[= 0 - \pi \sigma_0'' \epsilon_0\]
Tenga en cuenta que los componentes en fase no producen trabajo neto cuando se integran a lo largo de un ciclo, mientras que los componentes fuera de fase dan como resultado una disipación neta por ciclo igual a:
\[W_{dis} = \pi \sigma_0'' \epsilon_0 = \pi \sigma_0 \epsilon_0 \sin \delta\]
Esto debe interpretarse para ilustrar que la energía de deformación asociada con la tensión y deformación en fase es reversible; es decir, que la energía que se almacena en el material durante un ciclo de carga puede recuperarse sin pérdida durante la descarga. Por el contrario, la energía suministrada al material por los componentes desfasados se convierte irreversiblemente en calor.
La energía máxima almacenada por los componentes en fase ocurre en el punto del cuarto de ciclo, y esta energía máxima almacenada es:
\[\begin{array} {rcl} {W_{st}} & = & {\int_{0}^{\pi /2\omega} (\sigma_0' \cos \omega t)(-\epsilon_0 \omega \sin \omega t) dt} \\ {} & = & {-\dfrac{1}{2} \sigma_0' \epsilon_0 = -\dfrac{1}{2} \sigma_0 \epsilon_0 \cos \delta} \end{array}\]
La disipación relativa - la relación de\(W_{dis}/W_{st}\) - se relaciona entonces con el ángulo de fase por:
\[\dfrac{W_{dis}}{W_{st}} = 2\pi \tan \delta\]
También nos resultará conveniente expresar las funciones armónicas de tensión y deformación como exponenciales:
\[\sigma = \sigma_0^* e^{i \omega t}\]
\[\epsilon = \epsilon_0^* e^{i \omega t}\]
El\(e^{i \omega t}\) factor se desprende de la relación de Euler\(e^{i\theta} = \cos \theta + i \sin \theta\), y escribir tanto la tensión como la deformación como números complejos elimina la restricción de colocar el origen en un momento de máxima deformación como se hizo anteriormente. El módulo complejo ahora se puede escribir simplemente como:
\[E^* = \sigma_0^* /\epsilon_0^*\]
4. Modelos Matemáticos para Respuesta Viscoelástica Lineal
4.1 El modelo Maxwell Spring-Dashpot
La dependencia del tiempo de la respuesta viscoelástica es análoga a la dependencia del tiempo de los circuitos eléctricos reactivos, y ambas pueden describirse mediante ecuaciones diferenciales ordinarias idénticas en el tiempo. Una forma conveniente de desarrollar estas relaciones y al mismo tiempo ayudar a visualizar movimientos moleculares emplea modelos de “primavera-dashpot”. Estos análogos mecánicos utilizan resortes “Hookean”, representados en la Figura 8 y descritos por
\(\sigma = k\epsilon\)
donde\(\sigma\) y\(\epsilon\) son análogas a la fuerza y desplazamiento del resorte, y la constante elástica\(k\) es análoga al módulo de Young\(E\);\(k\) por lo tanto, tiene unidades de\(N/m^2\). El resorte modela la deformación instantánea de unión del material, y su magnitud se relacionará con la fracción de energía mecánica almacenada reversiblemente como energía de deformación.
El proceso de desenrollamiento entrópico es de naturaleza fluida, y puede ser modelado por un “amortiguador newtoniano” también mostrado en la Figura 8, en el que la tensión produce no una deformación sino una tasa de deformación:
\(\sigma = \eta \dot{\epsilon}\)
Aquí el overdot denota diferenciación temporal y η es una viscosidad con unidades de\(N-s/m^2\). En muchas de las relaciones a seguir, será conveniente emplear la relación de viscosidad a rigidez:
\(\tau = \dfrac{\eta}{k}\)
La unidad de\(\tau\) es tiempo, y se verá que esta relación es una medida útil del tiempo de respuesta de la respuesta viscoelástica del material.
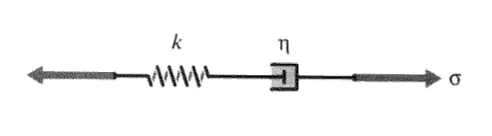
El sólido “Maxwell” mostrado en la Figura 9 es un modelo mecánico en el que un resorte Hookean y un amortiguador newtoniano están conectados en serie. El resorte debe visualizarse como representando el componente elástico o energético de la respuesta, mientras que el amortiguador representa el componente conformacional o entrópico. En una conexión en serie como el modelo Maxwell, la tensión en cada elemento es la misma e igual a la tensión impuesta, mientras que la deformación total es la suma de la deformación en cada elemento:
\(\sigma = \sigma_s = \sigma_d\)
\(\epsilon = \epsilon_s + \epsilon_d\)
Aquí los subíndices\(s\) y\(d\) representan la primavera y el dashpot, respectivamente. Al buscar una única ecuación que relacione la tensión con la deformación, es conveniente diferenciar la ecuación de deformación y luego escribir las tasas de deformación de resorte y amortiguador en términos de la tensión:
\(\dot{\epsilon} = \dot{\epsilon_s} + \dot{\epsilon_d} = \dfrac{\dot{sigma}}{k} + \dfrac{\sigma}{\eta}\)
Multiplicando por\(k\) y usando\(\tau = \eta /k\):
\[k \dot{\epsilon} = \dot{\sigma} + \dfrac{1}{\tau} \sigma\]
Esta expresión es una ecuación “constitutiva” para nuestro material ficticio de Maxwell, una ecuación que relaciona la tensión con la tensión. Obsérvese que contiene derivados del tiempo, por lo que no existe una constante simple de proporcionalidad entre tensión y deformación. El concepto de “módulo” —la relación entre tensión y deformación— debe ampliarse para dar cuenta de este comportamiento más complicado.
La ecuación 5.4.22 puede resolverse para la tensión\(\sigma (t)\) una vez especificada la deformación\(\epsilon (t)\), o para la deformación si se especifica la tensión. Dos ejemplos ilustrarán este proceso:
Ejemplo\(\PageIndex{2}\)
En una prueba de relajación de esfuerzo, una deformación constante\(\epsilon_0\) actúa como “entrada” al material, y buscamos una expresión para el estrés dependiente del tiempo resultante; esto se representa en la Figura 10.
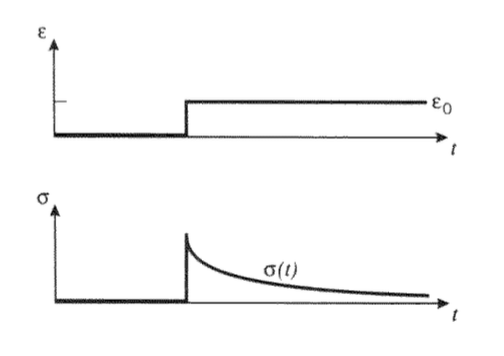
Ya que en la relajación de estrés\(\dot{\epsilon} = 0\), la ecuación 5.4.22 se convierte
\(\dfrac{d \sigma}{dt} = -\dfrac{1}{\tau} \sigma\)
Separación de variables e integración:
Aquí es evidente la significación del\(\tau \equiv \eta /k\) “tiempo de relajación” característico; es físicamente el tiempo necesario para que el estrés caiga a\(1/e\) su valor inicial. También es el momento en el que la función de tensión pasa por una inflexión cuando se grafica contra el tiempo logarítmico.
El módulo de relajación se\(E_{rel}\) puede obtener de esta relación directamente, señalando que inicialmente solo el resorte se deformará y la tensión inicial y la deformación están relacionadas por\(\sigma_0 = k \epsilon_0\). Entonces
\(E_{rel} (t) = \dfrac{\sigma(t)}{\epsilon_0} = \dfrac{\sigma_0}{\epsilon_0} \exp (-t/\tau)\)
\[E_{rel} (t) = k \exp (-t/\tau)\]
Esta importante función se representa esquemáticamente en la Figura 11. Los dos parámetros ajustables en el modelo,\(k\) y\(\tau\), se pueden utilizar para forzar al modelo a que coincida con una gráfica experimental del módulo de relajación en dos puntos. La rigidez del resorte se\(k\) establecería en el módulo inicial o de vidrio\(E_g\), y se\(\tau\) elegiría para forzar el valor\(k/e\) a coincidir con los datos experimentales en\(t = \tau\).
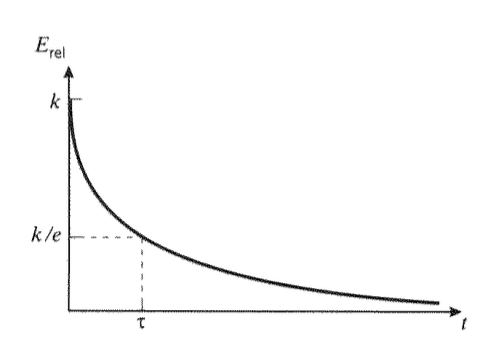
El tiempo\(\tau\) de relajación depende fuertemente de la temperatura y otros factores que afectan la movilidad del material, y es aproximadamente inverso a la velocidad de movimiento molecular. Arriba\(T_g\),\(\tau\) es muy corto; abajo\(T_g\), es muy largo. Se dará una consideración más detallada de la dependencia de la temperatura en una sección posterior, en el contexto de materiales “termorreológicamente simples”.
Ejemplo\(\PageIndex{3}\)
En el caso de la respuesta dinámica, la dependencia del tiempo tanto de la tensión como de la deformación son de la forma\(\exp (i \omega t)\). Por tanto, todas las derivadas de tiempo contendrán la expresión\((i \omega) \exp (i \omega t)\), por lo que la Ecuación 5.4.22 da
\(k (i \omega) \epsilon_0^* \exp (i \omega t) = (i \omega + \dfrac{1}{\tau_j}) \sigma_0^* \exp (i \omega t)\)
El módulo complejo\(E^*\) es entonces
\[E^* = \dfrac{\sigma_0^*}{\epsilon_0^*} = \dfrac{k(i\omega)}{i \omega + \tfrac{1}{\tau_j}} = \dfrac{k(i\omega \tau)}{1 + i \omega \tau}\]
Esta ecuación puede ser manipulada algebraicamente (multiplicar y dividir por el complejo conjugado del denominador) para producir:
\[E^* = \dfrac{k\omega^2 \tau^2}{1 + \omega^2 \tau^2} + i \dfrac{k \omega \tau}{1 + \omega^2 \tau^2}\]
En la Ecuación 5.4.25, se dan explícitamente los componentes real e imaginario del módulo complejo; estas son las relaciones “Debye” también importantes en la teoría de circuitos.
4.2 El sólido lineal estándar (forma Maxwell)
La mayoría de los polímeros no presentan el flujo irrestricto permitido por el modelo Maxwell, aunque podría ser un modelo razonable para Silly Putty o alquitrán caliente. Por lo tanto, la Ecuación 5.4.23 es válida sólo para un conjunto muy limitado de materiales. Para polímeros más típicos cuyo cambio conformacional está eventualmente limitado por la red de enredos u otros tipos de puntos de unión, se pueden usar modelos de amortiguadores de resorte más elaborados de manera efectiva.
Colocar un resorte en paralelo con la unidad Maxwell da un modelo muy útil conocido como el “Sólido Lineal Estándar” (S.L.S.) mostrado en la Figura 12. Este resorte tiene rigidez\(k_e\), llamado así porque proporciona un “equilibrio” o rigidez gomosa que permanece después de que las tensiones en el brazo Maxwell se hayan relajado a medida que se extiende el amortiguador.
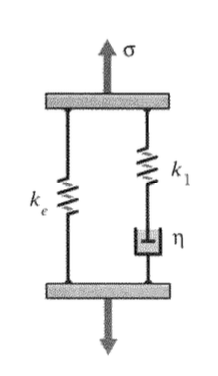
En esta disposición, el brazo Maxwell y el resorte paralelo\(k_e\) experimentan la misma deformación, y la tensión total\(\sigma\) es la suma de la tensión en cada brazo:\(\sigma = \sigma_e + \sigma_m\). Es incómodo resolver el estrés\(\sigma_m\) en el brazo Maxwell usando la Ecuación 5.4.22, ya que contiene tanto el estrés como su derivada del tiempo. La transformación de Laplace es muy conveniente en este y otros problemas de viscoelasticidad, ya que reduce las ecuaciones diferenciales a las algebraicas. Apéndices A enumera algunos pares de transformaciones que se encuentran a menudo en estos problemas.
Dado que la tensión y la deformación son cero a medida que se aproxima el origen desde la izquierda, las transformaciones de las derivadas del tiempo son solo la variable de Laplace s veces las transformaciones de las funciones; denotando las funciones transformadas con un overline, tenemos\(\mathcal{L} (\dot{\epsilon}) = s \bar{\epsilon}\) y\(\mathcal{L} (\dot{\sigma}) = s \bar{\sigma}\). Luego, escribir la transformación de una expresión como la Ecuación 5.4.22 se realiza simplemente colocando una línea sobre las funciones dependientes del tiempo, y reemplazando el overdot derivado del tiempo por un coeficiente s:
\(k \dot{\epsilon} = \dot{\sigma_m} + \dfrac{1}{\tau} \sigma_m \to k_1 s \bar{\epsilon} = s \bar{\sigma_m} + \dfrac{1}{\tau} \bar{\sigma_m}\)
Resolviendo para\(\bar{\sigma_{m}}\):
\[\bar{\sigma_m} = \dfrac{k_1 s}{s + \tfrac{1}{\tau}} \bar{\epsilon}\]
Añadiendo el estrés\(\bar{\sigma_e} = k_e \bar{\epsilon}\) en el resorte de equilibrio, el estrés total es:
\(\bar{\sigma} = k_e \bar{\epsilon} + \dfrac{k_1 s}{s + \tfrac{1}{\tau}} \bar{\epsilon} = \left \{ k_e + \dfrac{k_1 s}{s + \tfrac{1}{\tau}} \right \} \bar{\epsilon}\)
Este resultado puede ser escrito
\[\bar{\sigma} = \mathcal{E} \bar{\epsilon}\]
donde para este modelo el parámetro\(\mathcal{E}\) es
\[\mathcal{E} = k_e + \dfrac{k_1 s}{s + \tfrac{1}{\tau}}\]
La ecuación 5.4.27, que recuerda claramente a la Ley de Hooke\(\sigma = E_{\epsilon}\) pero en el plano de Laplace, se denomina ecuación constitutiva viscoelástica asociada. Aquí la expresión específica para\(\mathcal{E}\) es la del modelo Standard Lineal Solid, pero también se podrían haber utilizado otros modelos.
Para una función de entrada de deformación dada\(\epsilon (t)\), obtenemos la función de tensión resultante en tres pasos:
1. Obtener una expresión para la transformación de la función de deformación,\(\bar{\epsilon} (s)\).
2. Formar el producto algebraico\(\bar{\sigma} (s) = \mathcal{E} \bar{\epsilon} (s)\).
3. Obtener la transformación inversa del resultado para producir la función de esfuerzo en el plano de tiempo.
Ejemplo\(\PageIndex{4}\)
En el caso de la relajación del estrés, la función de deformación\(\epsilon (t)\) se trata como una constante\(\epsilon_0\) multiplicada por la función “Heaviside” o “paso unitario”\(u(t)\):
\(\epsilon (t) = \epsilon_0 u(t), \ \ \ \ u(t) = \begin{cases} 0, & t < 0\\ 1, & t \ge 0\end{cases}\)
Esto tiene la transformación de Laplace
\(\bar{\epsilon} = \dfrac{\epsilon_0}{s}\)
Usando esto en la Ecuación 5.4.27 y dividiendo por\(\epsilon_0\), tenemos
\(\dfrac{\bar{\sigma}}{\epsilon_0} = \dfrac{k_e}{s} + \dfrac{k_1}{s + \tfrac{1}{\tau}}\)
Ya que\(\mathcal{L}^{-1} 1/(s + a) = e^{-at}\), esto se puede invertir directamente para dar
\[\dfrac{\sigma (t)}{\epsilon_0} \equiv E_{rel} (t) = k_e + k_1 \exp (-t/\tau)\]
Esta función, que es justamente la del modelo Maxwell desplazado hacia arriba en una cantidad\(k_e\), se utilizó para generar la curva mostrada en la Figura 6.
Ejemplo\(\PageIndex{5}\)
La forma de la Ecuación 5.4.27 es conveniente cuando se desea la tensión necesaria para generar una deformación dada. Es algo incómodo cuando se desea la deformación generada por una tensión dada, ya que entonces el parámetro\(\mathcal{E}\) aparece en el denominador:
\(\bar{\epsilon} = \dfrac{\bar{\sigma}}{\mathcal{E}} = \dfrac{\bar{\sigma}}{k_e + \dfrac{k_1 s}{s + \tfrac{1}{\tau}}}\)
Esto es más difícil de invertir, y en tales casos\(^{\text{TM}}\) puede ser útil un software de manipulación simbólica como Maple. Por ejemplo, si queremos calcular el cumplimiento de fluencia del Sólido Lineal Estándar Maxwell, podríamos escribir:
read transformation library
> with(inttrans):
define governing equation
> eq1:=sigbar=EE*epsbar;
Constant stress sig0:
> sigbar:=laplace(sig0,t,s);
EE viscoelastic operator - Maxwell S.L.S. model
> EE:= k[e]+k[1]*s/(s+1/tau);
Solve governing equation for epsbar and invert:
> C[crp](t):=simplify((invlaplace(solve(eq1,epsbar),s,t))/sig0);
k[e] t
-k[e] - k[1] + k[1] exp(- -------------------)
tau (k[e] + k[1])
C[crp](t) := - -----------------------------------------------
k[e] (k[e] + k[1])
Este resultado se puede escribir como
\[C_{crp} (t) = C_g + (C_r - C_g) (1 - e^{-t/\tau_c})\]
donde
\(C_g = \dfrac{1}{k_e + k_1}, \ \ C_r = \dfrac{1}{k_e}, \ \ \tau_c = \tau (\dfrac{k_e + k_1}{k_e})\)
El cumplimiento vítreo\(C_g\) es el cumplimiento de los dos resortes\(k_e\) y que\(k_1\) actúa en paralelo, y el cumplimiento gomoso\(C_r\) es el del resorte\(k_e\) solo, como se esperaba. Menos obvio es que el tiempo característico para la fluencia\(\tau_c\) (a veces llamado el tiempo de “retraso”) es más largo que el tiempo característico para la relajación\(\tau\), por un factor igual a la relación del módulo vítreo al cauchoso. Este es un resultado general, no restringido al modelo particular utilizado.
Se produce una forma menos incómoda para los problemas de cumplimiento cuando se utilizan modelos “tipo Voigt” en lugar de modelos tipo Maxwell; consulte Ejercicio\(\PageIndex{7}\) y Ejercicio\(\PageIndex{8}\).
El Sólido Lineal Estándar es un modelo de tres parámetros capaz de describir las características generales de la relajación viscoelástica:\(k_e\) y\(k_1\) se eligen para ajustarse a los módulos vítreos y gomosos, y\(\tau\) se elige para colocar la relajación en el intervalo de tiempo correcto:
\[k_e = E_r\]
\[k_1 = E_g - E_r\]
\[\tau = t @ E_{rel} = (E_r + \dfrac{1}{e} (E_g - E_r))\]
Esto obliga a que la predicción de S.L.S. coincida con los datos experimentales en tres puntos, pero la capacidad del modelo para ajustarse a los datos experimentales en todo el rango de relajación suele ser pobre. El módulo de relajación predicho por el S.L.S. cae de\(E_g\) a\(E_r\) en aproximadamente dos décadas (Una “década” de tiempo en nuestro contexto es un múltiplo de diez, digamos de 103 a 104 segundos, en lugar de un lapso de diez años.) de tiempo, que generalmente es una transición demasiado abrupta.
4.3 El modelo Wiechert
Un polímero real no se relaja con un solo tiempo de relajación como lo predijeron los modelos anteriores. Los segmentos moleculares de longitud variable contribuyen a la relajación, con los segmentos más simples y cortos relajándose mucho más rápidamente que los largos. Esto conduce a una distribución de los tiempos de relajación, lo que a su vez produce una relajación extendida a lo largo de un tiempo mucho más largo del que se puede modelar con precisión con un solo tiempo de relajación. Cuando el ingeniero considera necesario incorporar este efecto, el modelo Wiechert ilustrado en la Figura 13 puede tener tantos elementos Maxwell de amortiguador de resorte como sean necesarios para aproximar satisfactoriamente la distribución.
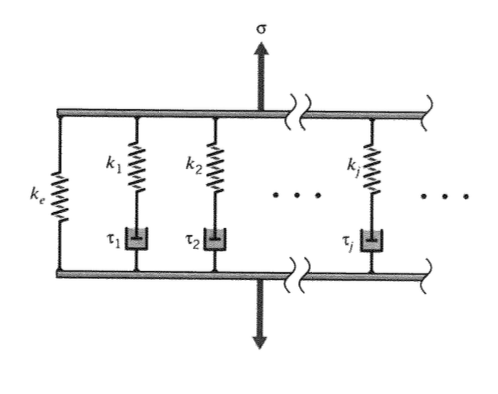
La tensión total\(\sigma\) transmitida por el modelo es la tensión en el resorte aislado (de rigidez\(k_e\)) más que en cada uno de los brazos de amortiguador de resorte Maxwell:
\(\sigma = \sigma_e + \sum_j \sigma_j\)
De la Ecuación 5.4.26, la tensión en el brazo Maxwell es
\(\overline{\sigma_j} = \dfrac{k_j s \bar{\epsilon}}{(s + \tfrac{1}{\tau_j})}\)
Entonces
\[\bar{\sigma} = \bar{\sigma}_e + \sum_j \bar{\sigma}_j = \left \{ k_e + \sum_j \dfrac{k_j s}{(s + \tfrac{1}{\tau_j})} \right \} \bar{\epsilon}\]
La cantidad en tirantes es el operador de módulo viscoelástico\(\mathcal{E}\) definido en la Ecuación 5.4.27 para el modelo Wiechert.
Ejemplo\(\PageIndex{6}\)
En las pruebas de relajación de estrés, tenemos
\(\epsilon (t) = \epsilon_0 \Rightarrow \bar{\epsilon} (s) = \epsilon_0/s\)
\(\bar{\sigma} (s) = \mathcal{E} (s) \bar{\epsilon} (s) = \left \{ k_e + \sum_j \dfrac{k_j s}{s + \tfrac{1}{\tau_j}} \right\} \dfrac{\epsilon_0}{s} = \left \{ \dfrac{k_e}{s} + \sum_j \dfrac{k_j}{s + \tfrac{1}{\tau_j}}\right\} \epsilon_0\)
\[\sigma (t) = \mathcal{L}^{-1} [\bar{\sigma} (s)] = \left \{k_e + \sum_j k_j \exp (\dfrac{-t}{\tau_j}) \right \} \epsilon_0\]
Dividiendo por\(\epsilon_0\), el módulo de relajación es
\[E_{rel} (t) = k_e + \sum_j k_j \exp (\dfrac{-t}{\tau_j})\]
Las constantes materiales en esta expresión (\(k_e\)y las diversas\(k_j\) y\(\tau_j\)) se pueden seleccionar forzando los valores predichos de Erel (t) dados por la Ecuación 5.4.36 para que coincidan con los determinados experimentalmente. \(\PageIndex{19}\)El ejercicio proporciona un ejemplo de tal procedimiento.
Ejemplo\(\PageIndex{7}\)
Considere la función de esfuerzo resultante de una prueba de tasa de deformación constante:
\(\epsilon = R_{\epsilon} t \to \bar{\epsilon} (s) = R_{\epsilon}/s^2\)
donde\(R_{\epsilon}\) está la tasa de deformación. Entonces
\(\bar{\sigma} = \mathcal{E} (s) \bar{\epsilon} (s) = \left [k_e + \sum_j \dfrac{k_j s}{s + \tfrac{1}{\tau_j}} \right ] \dfrac{R_{\epsilon}}{s^2} = \dfrac{k_e R_{\epsilon}}{s^2} + \sum_j \dfrac{k_j R_{\epsilon}}{s(s + \tfrac{1}{\tau_j})}\)
\[\sigma (t) = k_e R_{\epsilon} t + \sum_j k_j R_{\epsilon} \tau_j [1 - \exp (-t/\tau_j)]\]
Tenga en cuenta que la función tensión-tiempo, y por lo tanto la curva de tensión-deformación, no es lineal. No es cierto, por lo tanto, que un diagrama curvo de tensión-deformación implique que la respuesta del material es no lineal. También es interesante observar que la pendiente de la curva de tensión-deformación constante-velocidad está relacionada con el valor del módulo de relajación evaluado al mismo tiempo:
\(\dfrac{d \sigma}{d \epsilon} = \dfrac{d\sigma}{dt} \cdot \dfrac{dt}{d\epsilon} = \dfrac{d\sigma}{dt} \cdot \dfrac{1}{R_{\epsilon}} = \left [k_e R_{\epsilon} + \sum_j k_j R_{\epsilon} \exp (-t/\tau_j) \right ] \dfrac{1}{R_{\epsilon}}\)
\[= \left [ k_e + \sum_j k_j \exp (-t/\tau_j) \right ] \equiv E_{rel} (t) |_{t = \epsilon/R_{\epsilon}}\]
Ejemplo\(\PageIndex{8}\)
Puede ser que la función de deformación de entrada no se conozca como una expresión matemática, o su expresión matemática puede ser tan complicada que hace que el proceso de transformación sea intratable. En esos casos, se puede volver a la ecuación constitutiva diferencial y refundirla en forma de diferencia finita para obtener una solución numérica. Recordemos que el estrés en el brazo\(j\) th del modelo Wiechert viene dado por
\[\dfrac{d \sigma_j}{dt} + \dfrac{1}{\tau_j} \sigma_j = k_j \dfrac{d\epsilon}{dt}\]
Esto se puede escribir en forma de diferencia finita como
\[\dfrac{\sigma_j^t - \sigma_j^{t - 1}}{\Delta t} + \dfrac{1}{\tau_j} \sigma_j^t = k_j \dfrac{\epsilon^t - \epsilon^{t - 1}}{\Delta t}\]
donde los superíndices\(t\) e\(t - l\) indican valores antes y después del paso de un pequeño incremento de tiempo\(\Delta t\). Resolviendo para\(\sigma_j^t\):
\[\sigma_j^t = \dfrac{1}{1 + (\Delta t/\tau_j)} [k_j (\epsilon^t - \epsilon^{t - 1}) + \sigma_j^{t - 1}]\]
Ahora sumando todos los brazos del modelo y agregando la tensión en el resorte de equilibrio:
\[\sigma^t = k_e \epsilon^t + \sum_j \dfrac{k_j (\epsilon^t - \epsilon^{t - 1}) + \sigma_j^{t - 1}}{1 + (\Delta t/\tau_j)}\]
Esto constituye un algoritmo recursivo que la computadora puede utilizar para calcular valores sucesivos de\(\sigma^t\) inicio en\(t = 0\). Además de almacenar los diversos\(k_j\) y\(\tau_j\) que constituyen la descripción del material, la computadora también debe guardar los valores anteriores de cada esfuerzo de brazo (el\(\sigma_j^{t-1}\)) en almacenamiento.
4.4 La Superposición de Boltzman Integral
Como se vio en las secciones anteriores, la viscoelasticidad lineal se puede afirmar en términos de modelos mecánicos construidos a partir de muelles lineales y dashpots. Estos modelos generan relaciones constitutivas que son ecuaciones diferenciales ordinarias; ver Ejercicio\(\PageIndex{13}\) y Ejercicio\(\PageIndex{14}\) como ejemplos de ello. Sin embargo, también se podrían usar ecuaciones integrales, y este enfoque integral también se usa como punto de partida para la teoría viscoelástica.
Las integrales son operaciones sumadoras, y esta visión de la viscoelasticidad toma la respuesta del material en el tiempo t como la suma de las respuestas a las excitaciones impuestas en todos los tiempos anteriores. La capacidad de sumar estas respuestas individuales requiere que el material obedezca una declaración de linealidad más general de la que hemos invocado anteriormente, específicamente que la respuesta a una serie de excitaciones individuales sea la suma de las respuestas que habrían sido generadas por cada excitación actuando sola. Matemáticamente, si el estrés debido a una cepa\(\epsilon_1 (t)\) es\(\sigma (\epsilon_1)\) y eso debido a una cepa diferente\(\epsilon_2 (t)\) es\(\sigma (\epsilon_2)\), entonces el estrés debido a ambas cepas es\(\sigma (\epsilon_1 + \epsilon_2) = \sigma (\epsilon_1) + \sigma (\epsilon_2)\). Combinando esto con la condición de escalado multiplicativo utilizada anteriormente, tenemos como declaración general de viscoelasticidad lineal:
\[\sigma (a \epsilon_1 + b \epsilon_2) = a \sigma (\epsilon_1) + b\sigma (\epsilon_2)\]
De esta definición se desprende la declaración “Boltzman Superposición Integral” de respuesta viscoelástica lineal. Considere la tensión\(\sigma_1 (t)\) en el momento\(t\) debido a la aplicación de una pequeña deformación\(\Delta_{\epsilon_1}\) aplicada en un tiempo\(\xi_1\) anterior a\(t\); esto se da directamente de la definición del módulo de relajación como
Del mismo modo, la tensión\(\sigma_2 (t)\) debida a un incremento de deformación\(\Delta_{\epsilon_2}\) aplicado en un momento diferente\(\xi_2\) es
Si el material es lineal, el esfuerzo total en el tiempo\(t\) debido a ambos incrementos de deformación juntos se puede obtener por superposición de estos dos efectos individuales:
A medida que aumenta el número de incrementos de deformación aplicados para acercarse a una distribución continua, esto se convierte en:
\[\to \sigma(t) = \int_{-\infty}^{t} E_{rel} (t - \xi)d\epsilon =\int_{-\infty}^{t} E_{rel} (t - \xi) \dfrac{d\epsilon (\mathcal{E})}{d\mathcal{E}} d\mathcal{E}\]
Ejemplo\(\PageIndex{9}\)
En el caso de la tasa de deformación constante\((\epsilon (t) = R_{\epsilon} t)\) tenemos
\(\dfrac{d\epsilon (\xi)}{d\xi} = \dfrac{d(R_{\epsilon} \xi)}{d\xi} = R_{\epsilon}\)
Para la respuesta de materiales de S.L.S.\((E_{rel} (t) = k_e + k_1 \exp [-t/\tau])\),
La ecuación 5.4.44 da el estrés como
Las declaraciones de Maple para llevar a cabo estas operaciones podrían ser:
define relaxation modulus for S.L.S. >Erel:=k[e]+k[1]*exp(-t/tau); define strain rate >eps:=R*t; integrand for Boltzman integral >integrand:=subs(t=t-xi,Erel)*diff(subs(t=xi,eps),xi); carry out integration >’sigma(t)’=int(integrand,xi=0..t);
lo que da el resultado:
Esto es idéntico a la Ecuación 5.4.37, con un brazo en el modelo.
La relación integral de Boltzman se puede obtener formalmente recordando que el módulo de relajación transformado se relaciona simplemente con el módulo viscoelástico asociado en el plano de Laplace como
relajación del estrés:\(\epsilon (t) = \epsilon_0 u(t) \to \bar{\epsilon = \dfrac{\epsilon_0}{s}\)
\(\bar{\sigma} = \mathcal{E} \bar{\epsilon} = \mathcal{E} \dfrac{\epsilon_0}{s}\)
\(\dfrac{\bar{\sigma}}{\epsilon_0} = \bar{E}_{rel} (s) = \dfrac{1}{s} \mathcal{E} (s)\)
Ya que\(s\bar{f} = \bar{\dot{f}}\), se mantienen las siguientes relaciones:
\(\bar{\sigma} = \mathcal{E} \bar{\epsilon} = s \bar{E}_{rel} \bar{\epsilon} = \bar{\dot{E}}_{rel} \bar{\epsilon} = \bar{E}_{rel} \bar{\dot{\epsilon}}\)
Los dos últimos de lo anterior son de la forma para la que se aplica la transformación integral de convolución (ver Apéndice A), por lo que se obtienen inmediatamente las siguientes cuatro relaciones equivalentes:
\[\begin{array} {rcl} {\sigma (t)} & = & {\int_0^t E_{rel} (t - \xi) \dot{\epsilon} (\xi) d \xi} \\ {} & = & {\int_0^t E_{rel} (\xi) \dot{\epsilon} (t - \xi) d \xi} \\ {} & = & {\int_0^t \dot{E}_{rel} (t - \xi) \epsilon (\xi) d \xi} \\ {} & = & {\int_0^t \dot{E}_{rel} (\xi) \epsilon (t - \xi) d \xi} \end{array}\]
Estas relaciones son formas de la fórmula de Duhamel, donde se\(E_{rel}(t)\) puede interpretar como la tensión\(\sigma (t)\) resultante de una entrada unitaria de deformación. Si el estrés en lugar de la deformación es la cantidad de entrada, entonces un desarrollo análogo conduce a
\[\epsilon (t) = \int_0^t C_{crp} (t - \xi) \dot{sigma} (\xi) d \xi\]
donde\(C_{crp} (t)\), la respuesta de deformación a una entrada de tensión unitaria, es la cantidad definida anteriormente como la conformidad de fluencia. La relación entre el cumplimiento de fluencia y el módulo de relajación se puede desarrollar ahora como:
\(\bar{\sigma} = s \bar{E}_{rel} \bar{\epsilon}\)
\(\bar{\epsilon} = s \bar{C}_{crp} \bar{\sigma}\)
\(\bar{\sigma} \bar{\epsilon} = s^2 \bar{E}_{rel} \bar{C}_{crp} \bar{\epsilon} \bar{\sigma} \to \bar{E}_{rel} \bar{C}_{crp} = \dfrac{1}{s^2}\)
Se ve que se debe resolver una ecuación integral para obtener una función de fluencia a partir de una función de relajación, o viceversa. Este proceso de deconvolución a veces se puede realizar analíticamente (probablemente usando transformaciones de Laplace), y en casos intratables se ha hecho algún uso de enfoques numericos.
4.5 Efecto de la temperatura
Como se mencionó al principio (\(cf\). Ecuación 5.4.2), la temperatura tiene una influencia dramática en las tasas de respuesta vis- coelástica, y en el trabajo práctico a menudo es necesario ajustar un análisis viscoelástico para variar la temperatura. Esta fuerte dependencia de la temperatura también puede ser útil en la caracterización experimental: si por ejemplo una transición viscoelástica ocurre demasiado rápido a temperatura ambiente para facilitar la medición, el experimentador puede bajar la temperatura para ralentizar las cosas.
En algunos polímeros, especialmente los materiales “simples” como el poliisobutileno y otros termoplásticos amorfos que tienen pocas características de complicación en su microestructura, la relación entre el tiempo y la temperatura puede describirse mediante modelos correspondientemente simples. Tales mate- riales se califican de “termorreológicamente simples”.
Para materiales tan simples, el efecto de bajar la temperatura es simplemente desplazar la respuesta viscoelástica (trazada contra el tiempo logarítmico) hacia la derecha sin cambio de forma. Esto equivale a incrementar el tiempo de relajación\(\tau\), por ejemplo en Eqns. 5.4.29 o 5.4.30, sin cambiar los módulos o cumplimientos vítreos o gomosos. Un “factor de desplazamiento tiempo-temperatura”\(a_T (T)\) puede definirse como el desplazamiento horizontal que debe aplicarse a una curva de respuesta\(C_{crp} (t)\), digamos, medida a una temperatura\(T\) arbitraria para moverla a la curva medida a alguna temperatura de referencia\(T_{ref}\).
\[\log (a_T) = \log \tau (T) - \log \tau (T_{ref})\]
Este desplazamiento se muestra esquemáticamente en la Figura 14.
Figura 14: El factor de desplazamiento tiempo-temperatura.
En lo anterior asumimos un solo tiempo de relajación. Si el modelo contiene múltiples tiempos de relajación, la simplicidad termorreológica exige que todos tengan el mismo factor de desplazamiento, ya que de lo contrario la curva de respuesta cambiaría tanto de forma como de posición a medida que se varía la temperatura.
Si el tiempo de relajación obedece a una relación Arrhenius de la forma\(\tau (T) = \tau_0 \exp (E^{\dagger}/RT)\), se demuestra fácilmente que el factor de desplazamiento es (ver Ejercicio\(\PageIndex{17}\))
\[\log a_T = \dfrac{E^{\dagger}}{2.303 R} (\dfrac{1}{T} - \dfrac{1}{T_{ref}})\]
Aquí el factor\(2.303 = \ln 10\) es la conversión entre logaritmos naturales y base 10, los cuales se utilizan comúnmente para facilitar el trazado gráfico utilizando papel de registro.
Si bien el tratamiento cinético de Arrhenius suele ser aplicable a las transiciones de polímeros secundarios, muchos trabajadores sienten que la transición primaria vidrio-caucho parece regida por otros principios. Una alternativa popular es usar la ecuación “W.L.F.” a temperaturas cercanas o superiores a la temperatura del vidrio:
\[\log a_T = \dfrac{-C_1 (T- T_{ref}}{C_2 + (T - T_{ref})}\]
Aquí\(C_1\) y\(C_2\) son constantes materiales arbitrarias cuyos valores dependen del material y la elección de la temperatura de referencia\(T_{ref}\). Se ha encontrado que si\(T_{ref}\) se elige que sea\(T_g\), entonces\(C_1\) y\(C_2\) a menudo asumen valores “universales” aplicables a una amplia gama de polímeros:
\[\log a_T = \dfrac{-17.4 (T - T_g)}{51.6 + (T- T_g)}\]
donde\(T\) está en Celsius. El artículo original de W.L.F. (M.L. Williams, R.F. Landel, y J.D. Ferry, J. Am. Chem. Soc., Vol. 77, No. 14, pp. 3701—3707, 1955.) desarrolló esta relación empíricamente, pero la racionalizó en términos de conceptos de volumen libre.
Una serie de datos de fluencia o relajación tomados en un rango de temperaturas se pueden convertir en una sola “curva maestra” a través de este desplazamiento horizontal. Se elige una curva particular como referencia, luego las otras curvas se desplazan horizontalmente para obtener una sola curva que abarca un amplio rango de tiempo logarítmico como se muestra en la Figura 15. Las curvas que representan datos obtenidos a temperaturas inferiores a la temperatura de referencia aparecen en tiempos más largos, a la derecha de la curva de referencia, por lo que tendrán que desplazarse hacia la izquierda; este es un desplazamiento positivo ya que hemos definido el factor de desplazamiento en la Ecuación 5.4.47. Cada curva produce su propio valor de\(a_T\), por lo que\(a_T\) se convierte en una función tabulada de la temperatura. La curva maestra es válida solo a la temperatura de referencia, pero se puede usar a otras temperaturas desplazándola por el valor apropiado de log\(a_T\).
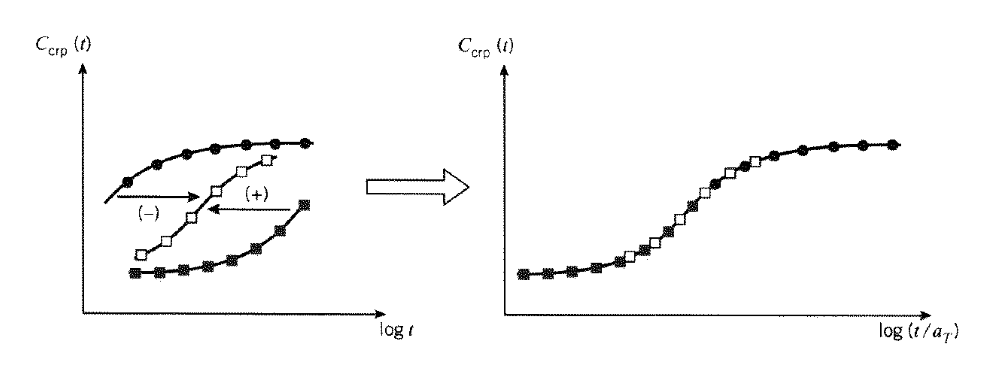
El etiquetado de las abscisas como\(\log(t/a_T) = \log t - \log a_t\) en la Figura 15 merece alguna discusión. En lugar de desplazar la curva maestra hacia la derecha para temperaturas menores que la temperatura de referencia, o hacia la izquierda para temperaturas más altas, es más fácil simplemente renumerar el eje, aumentando los números para bajas temperaturas y disminuyéndolas para altas. Por lo tanto, la etiqueta indica que los valores numéricos en el eje horizontal se han ajustado para la temperatura restando el log del factor de desplazamiento. Dado que las temperaturas más bajas tienen factores de cambio positivos, los números son más pequeños de lo que necesitan ser y tienen que ser aumentados por el factor de cambio apropiado. Etiquetar los ejes de esta manera es indudablemente ambiguo y tiende a ser confuso, pero el ajuste correcto se realiza fácilmente recordando que temperaturas más bajas ralentizan la tasa de fluencia, por lo que los tiempos tienen que hacerse más largos al aumentar los números en el eje. Por el contrario, para temperaturas más altas, los números deben hacerse más pequeños.
Ejemplo\(\PageIndex{10}\)
Deseamos encontrar el grado de fluencia en un ciclo de dos temperaturas que consiste en\(t_1 = 10\) horas a las 20\(^{\circ}C\) seguidas de\(t_2 = 5\) minutos a las 50\(^{\circ}C\). Se sabe que el factor de desplazamiento logarítmico para 50\(^{\circ}C\), relativo a una temperatura de referencia de 20\(^{\circ}C\), es de -2.2.
Usando el factor de cambio dado, podemos ajustar el tiempo de la segunda temperatura\(^{\circ}C\) a 50 a un tiempo equivalente\(t_2'\) a 20 de la\(^{\circ}C\) siguiente manera:
\(t_2' = \dfrac{t_2}{a_T} = \dfrac{\text{5 min}}{10^{-2.2}} = 792 \text{ min} = 13.2 \text{ h}\)
De ahí que 5 minutos a 50\(^{\circ}C\) equivale a más de 13 h a las 20\(^{\circ}C\). El tiempo efectivo total es entonces la suma de los dos pasos de temperatura:
\(t' = t_1 + t_2' = 10 + 13.2 = 23.2 \text{ h}\)
La fluencia total ahora se puede evaluar utilizando este tiempo efectivo en una relación adecuada para fluencia, por ejemplo la Ecuación 5.4.30.
El enfoque de tiempo efectivo para la respuesta a temperaturas variables se puede extender a un número arbitrario de pasos de temperatura:
\(t' = \sum_j t_j' = \sum_j (\dfrac{t_j}{a_T (T_j)})\)
Para temperaturas dependientes del tiempo en general, tenemos\(T = T(t)\), por lo que\(a_T\) se convierte en una función implícita del tiempo. El tiempo efectivo se puede escribir para funciones continuas como
\[t' = \int_0^t \dfrac{d\xi}{a_T (\xi)}\]
donde\(\xi\) es una variable de tiempo ficticio. Este enfoque, aunque quizás parezca un poco abstracto, es de considerable utilidad en modelar la respuesta de los materiales dependientes del tiempo. Factores como el daño debido al estrés aplicado o la exposición ambiental pueden acelerar o retardar la velocidad de una respuesta dada, y este cambio en la tasa puede describirse por un factor de expansión en el tiempo similar a aT pero dependiente de otros factores además de la temperatura.
Ejemplo\(\PageIndex{11}\)
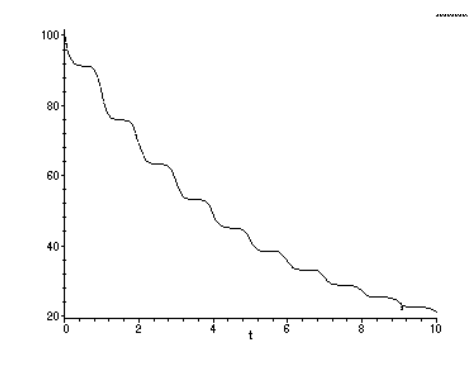
Considerar un polímero hipotético con un tiempo de relajación medido a 20\(^{\circ}C\) de\(\tau\) = 10 días, y con módulos vítreos y gomosos\(E_g = 100\),\(E_r = 10\). El polímero se puede tomar para obedecer la ecuación de W.L.F. con una precisión razonable, con\(T_g\) = 0\(^{\circ}C\). Deseamos calcular el módulo de relajación en el caso de una temperatura que varíe sinusoidalmente\(\pm\) 5\(^{\circ}\) alrededor de 20 en el\(^{\circ}C\) transcurso de un día. Esto se puede lograr usando el tiempo efectivo calculado a partir de la Ecuación 5.4.51 en la Ecuación 5.4.29, como se muestra en los siguientes comandos Maple:
define WLF form of log shift factor >log_aT:=-17.4*(T-Tg)/(51.6+(T-Tg)); find offset; want shift at 20C to be zero >Digits:=4;Tg:=0;offset:=evalf(subs(T=20,log_aT)); add offset to WLF >log_aT:=log_aT-offset; define temperature function >T:=20+5*cos(2*Pi*t); get shift factor; take antilog >aT:=10^log_aT; replace time with dummy time variable xi >aT:=subs(t=xi,aT); get effective time t’ >t_prime:=int(1/aT,xi=0..t); define relaxation modulus >Erel:=ke+k1*exp(-t_prime/tau); define numerical parameters >ke:=10;k1:=90;tau:=10; plot result >plot(Erel,t=0..10);
5 Análisis de Estrés Viscoelástico
5.1 Estados de tensión multiaxial
Las expresiones viscoelásticas anteriores han sido referenciadas a un estado de tensión simple en el que una muestra es sometida a tensión uniaxial. Esta carga está relacionada con las pruebas de caracterización de laboratorio, pero la información obtenida de estas pruebas debe moldearse en una forma que permita la aplicación a los estados de tensión multiaxiales que se encuentran en el diseño real.
Muchas fórmulas para la tensión y el desplazamiento en problemas de mecánica estructural se moldean en formas que contienen el módulo de Young\(E\) y la relación de Poisson\(ν\). Para adaptar estas relaciones a la respuesta viscoelástica, se puede observar tanto la respuesta longitudinal como la transversal en un ensayo de tracción, de manera que ambas\(E(t)\) y se\(ν(t)\) puedan determinar. Los modelos podrían entonces ajustarse a ambos modos de deformación para encontrar los operadores viscoelásticos correspondientes\(\mathcal{E}\) y\(\mathcal{N}\). Sin embargo, a menudo es más conveniente usar el módulo de cizallamiento\(G\) y el módulo aparente\(K\) en lugar de\(E\) y\(ν\), lo que se puede hacer usando las relaciones válidas para materiales elásticos lineales isotrópicos:
\[E= \dfrac{9GK}{3K + G}\]
\[v =\dfrac{3K - 2G}{6K + 2G}\]
Estas relaciones importantes se derivan de argumentos geométricos o de equilibrio, y no implican consideraciones de respuesta dependiente del tiempo. Dado que la transformación de Laplace afecta al tiempo y no a los parámetros espaciales, los operadores viscoelásticos correspondientes obedecen relaciones análogas en el plano de Laplace:
\(\mathcal{E} (s) = \dfrac{9\mathcal{G}(s) \mathcal{K}(s)}{3\mathcal{K}(s) + \mathcal{G}(s)}\)
Figura 17: Módulos de relajación de poliisobutileno en dilatación (\(K\)) y cizallamiento (\(G\)). De Huang, M.G., Lee, E.H., y Rogers, T.G., “Sobre la influencia de la compresibilidad viscoelástica en el análisis de estrés”, Informe Técnico de la Universidad de Stanford No. 140 (1963).
Estas sustituciones son útiles porque\(K(t)\) suele ser mucho mayor que\(G(t)\), y\(K(t)\) por lo general experimenta relajaciones mucho más pequeñas que\(G(t)\) (ver Figura 17). Estas observaciones conducen a idealizaciones de compresiblildad que simplifican enormemente el análisis. Primero, si uno toma\(K_{rel} = K_e\) ser finito pero constante (solo respuesta de cizallamiento viscoelástico), entonces
\(\mathcal{K} = s \bar{K}_{rel} = s \dfrac{K_e}{s} = K_e\)
En segundo lugar, si\(K\) se asume no solo constante sino infinita (material incompresible, sin deformación hidrostática), entonces
\(\mathcal{G} = \dfrac{\mathcal{E}}{3}\)
\(\mathcal{N} = v = \dfrac{1}{2}\)
Ejemplo\(\PageIndex{12}\)
Se observa que el módulo de cizallamiento del cloruro de polivinilo (PVC) se relaja de un valor vítreo de\(G_g = 800\) MPa a un valor gomoso de\(G_r =1.67\) MPa. El tiempo de relajación a los 75\(^{\circ} C\) es aproximadamente\(\tau =100\) s, aunque la transición es mucho más amplia de lo que sería predicho por un solo modelo de tiempo de relajación. Pero asumiendo un modelo sólido lineal estándar como aproximación, el operador de cizallamiento es
El módulo volumétrico es constante a una buena aproximación a\(K_e =1.33\) GPa. Estos datos se pueden utilizar para predecir la dependencia temporal de la relación de Poisson, usando la expresión
Al sustituir los valores numéricos y simplificar, esto se convierte
\(\mathcal{N} = 0.25 + \dfrac{9.97 \times 10^8}{4.79 \times 10^{11} s + 3.99 \times 10^9}\)
La relación de Poisson de “relajación”, la deformación dependiente del tiempo en una dirección inducida por una tensión constante en una dirección transversal, es entonces
\(\bar{v}_{rel} = \dfrac{\mathcal{N}}{s} = \dfrac{0.25}{s} + \dfrac{1}{s} (\dfrac{9.97 \times 10^8}{4.79 \times 10^{11} s + 3.99 \times 10^9})\)
Invirtiendo, esto da
Esta función se representa en la Figura 18. Se ve que la relación de Poisson aumenta de un valor vítreo de 0.25 a un valor gomoso de 0.5 a medida que el material se mueve del régimen vítreo al cauchoso con el tiempo. Tenga en cuenta que la constante de tiempo de 120 s en la expresión anterior no es lo mismo que el tiempo de relajación\(\tau\) para la respuesta de cizallamiento puro.
Figura 18: Dependencia del tiempo de la relación de Poisson para PVC a 75\(^{\circ} C\), asumiendo respuesta de cizallamiento viscoelástica y respuesta hidrostática elástica.
En el caso de la isotropía del material (propiedades no dependientes de la dirección de medición), a lo sumo serán necesarios dos operadores viscoelásticos\(\mathcal{K}\) —digamos\(\mathcal{G}\) y— para una caracterización completa del material. Para los materiales que presentan órdenes inferiores de simetría serán necesarios más descriptores: un material isotrópico transversalmente requiere cuatro descriptores constitutivos, un material ortotrópico requiere nueve y un material triclínico veintiuno. Si el material es a la vez viscoelástico y anisotrópico, estos son el número de operadores viscoelásticos que se requerirán. Claramente, el analista debe ser exigente para encontrar el equilibrio adecuado entre realismo y practicidad en la elección de modelos.
5.2 Superposición
Afortunadamente, a menudo es innecesario comenzar de cero en la solución de problemas de mecánica estructural que involucran materiales viscoelásticos. Describiremos dos métodos convenientes para adaptar soluciones estándar para materiales elásticos lineales a la caja viscoelástica, y el primero de ellos se basa en el principio de superposición de Boltzman. Ilustraremos esto con un ejemplo específico, el del recipiente a presión de pared delgada.
Los polímeros como el polibutileno y el cloruro de polivinilo están encontrando un uso creciente en plomería y otros sistemas de suministro de líquidos, y estos materiales exhiben una dependencia viscoelástica medible del tiempo en su respuesta mecánica. Es común ignorar estos efectos de velocidad en el diseño de sistemas simples mediante el uso de generosos factores de seguridad. Sin embargo, en situaciones más críticas el diseñador puede desear extender la teoría elástica esbozada en los textos estándar para incluir la viscoelasticidad del material.
Un punto importante para estresar al principio es que en muchos casos, la distribución de tensiones no depende de las propiedades del material y en consecuencia no está influenciada por la viscoelasticidad. Por ejemplo, la tensión de “aro”\(\sigma_{\theta}\) en un recipiente a presión cilíndrico abierto es
\(\sigma_{\theta} = \dfrac{pr}{b}\)
donde\(p\) está la presión interna,\(r\) es el radio del vaso, y\(b\) es el grosor de la pared. Si el material resulta ser viscoelástico, esta relación —que no contiene constantes materiales— se aplica sin cambios.
Sin embargo, los desplazamientos —por ejemplo el aumento del radio\(\delta_r\) — se ven afectados, aumentando con el tiempo a medida que aumenta la tensión en el material a través del cambio conformacional molecular. Para un recipiente cilíndrico abierto con material elástico lineal, la expansión radial es
\(\delta_r = \dfrac{pr^2}{bE}\)
El módulo elástico en el denominador indica que la expansión radial aumentará a medida que el material pierda rigidez a través de la respuesta viscoelástica. Al cuantificar este comportamiento, es conveniente reemplazar el módulo\(E\) por el cumplimiento\(C = 1/E\). La expresión para expansión radial tiene ahora la constante material en el numerador:
\[\delta_r = \dfrac{pr^2}{b} C\]
Si la presión\(p\) es constante, la viscoelasticidad entra en el problema solo a través del cumplimiento del material\(C\), que debe hacerse una función adecuada dependiente del tiempo. (Aquí asumimos que los valores de\(r\) y\(b\) pueden tratarse como constantes, lo que generalmente será válido para una buena aproximación). El valor de\(\delta_r\) en el tiempo\(t\) es entonces simplemente el factor\((pr^2/b)\) multiplicado por el valor de\(C(t)\) en ese momento.
La función\(C(t)\) necesaria aquí es la conformidad de fluencia del material, la deformación dependiente del tiempo exhibida por el material en respuesta a una tensión de tracción unitaria impuesta:\(C_{crp} = \epsilon (t)/\sigma_0\). El sólido lineal estándar, dado por la Ecuación 5.4.30, da el cumplimiento como
\[C_{crp} (t) = C_g + (C_r - C_g) (1 - e^{-t/\tau})\]
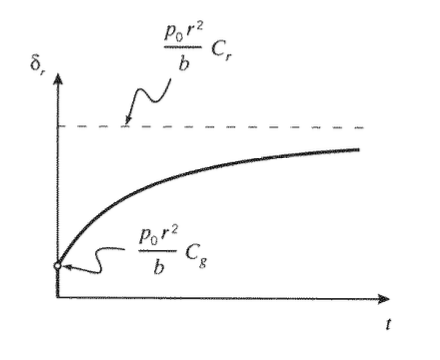
donde aquí se asume que el estrés se aplica en el momento\(t = 0\). La expansión radial de un recipiente a presión, sometido a una presión interna constante\(p_0\) y construido de un material para el cual el S.L.S. es un modelo razonable, es entonces
\[\delta_r (t) = \dfrac{p_0 r^2}{b} [C_g + (C_r - C_g) (1 - e^{-t/\tau}]\]
Esta función se muestra esquemáticamente en la Figura 19.
La situación es un poco más complicada si tanto la presión interna como el cumplimiento del material dependen del tiempo. Es incorrecto simplemente usar la ecuación anterior con el valor de\(p_0\) reemplazado por el valor de\(p(t)\) en un tiempo arbitrario, porque la expansión radial en el tiempo\(t\) está influenciada por la presión en tiempos anteriores así como la presión en el momento actual.
El procedimiento correcto es “plegar” las funciones de presión y cumplimiento juntas en una integral de convolución como se hizo en el desarrollo del Principio de Superposición de Boltzman. Esto da:
\[\delta_r (t) = \dfrac{r^2}{b} \int_{-\infty}^t C_{crp} (t - \xi) \dot{p} (\xi) d\xi\]
Ejemplo\(\PageIndex{13}\)
Que la presión interna sea una función de “rampa” en constante aumento, de modo que\(p = R_pt\), con\(R_p\) ser la tasa de incremento; entonces tenemos\(\dot{p} (\xi) = R_p\). Usando el sólido lineal estándar de la Ecuación 5.4.55 para la conformidad de fluencia, la tensión se calcula a partir de la integral de convolución como
Esta función se grafica en la Figura 20, para un material hipotético con parámetros\(C_g = 1/3 \times 10^5 \text{ psi}^{-1}\)\(C_r = 1/3 \times 10^4 \text{ psi}^{-1}\),\(b = 0.2\ in\),\(r = 2 \ in\),,\(\tau = 1\) mes y\(R_p = 100\) psi/mes. Tenga en cuenta que la tasa de fluencia aumenta de un valor inicial\((r^2/b)R_pC_g\) a un valor final a\((r^2/b)R_pC_r\) medida que los componentes elásticos vítreos se relajan.
Figura 20: Fluencia\(\delta_r(t)\) del hipotético recipiente a presión para aumentar constantemente la presión interna.
Cuando el recipiente a presión tiene extremos cerrados y, por lo tanto, debe resistir esfuerzos axiales y tangenciales, la expansión radial es\(\delta_r = (pr^2/bE) [1 − (ν/2)]\). La extensión de esta relación con la respuesta del material viscoelástico y una presión dependiente del tiempo es otro paso adelante en la complejidad. Ahora dos descriptores de material,\(E\) y\(ν\), deben ser modelados por funciones adecuadas dependientes del tiempo, y luego plegados en la función de presión. El enfoque de superposición descrito anteriormente podría usarse aquí también, pero con más complejidad algebraica. El “principio de correspondencia viscoelástica” que se presentará a continuación suele ser más sencillo, pero el concepto de superposición es muy importante para comprender la respuesta de los materiales dependientes del tiempo.
5.3 El principio de correspondencia viscoelástica
En los materiales elásticos, las tracciones y desplazamientos de límites pueden depender tanto del tiempo como de la posición sin afectar a la solución: el tiempo se lleva solo como parámetro, ya que no aparecen derivadas de tiempo en las ecuaciones gobernantes. Con materiales viscoelásticos, la ecuación constitutiva o tensión-deformación se sustituye por una ecuación diferencial de tiempo, lo que complica la solución posterior. En muchos casos, sin embargo, las ecuaciones de campo poseen ciertas propiedades matemáticas que permiten obtener una solución con relativa facilidad (E.H. Lee, “Viscoelasticidad”, Handbook of Engineering Mechanics, W. Flugge, ed., McGraw-Hill, Nueva York, 1962, Cap. 53.). El “principio de correspondencia viscoelástica” que se describe aquí funciona adaptando una solución elástica previamente disponible para que también sea aplicable a materiales viscoelásticos, de manera que una nueva solución desde cero sea innecesaria.
Si un problema mecánico —la estructura, sus materiales y sus condiciones límite de tracción y desplazamiento— se somete a la transformación de Laplace, a menudo ocurrirá que ninguno de los aspectos espaciales de su descripción se verá alterado: el problema aparecerá igual, al menos espacialmente. Sólo se alterarán los aspectos dependientes del tiempo, es decir, las propiedades del material. La versión del problema en el plano Laplace puede entonces interpretarse como que representa un problema de análisis de esfuerzos para un cuerpo elástico de la misma forma que el cuerpo viscoelástico, de manera que una solución para un cuerpo elástico se aplicará también a un cuerpo viscoelástico correspondiente, pero en el plano de Laplace.
Sin embargo, existe una excepción a esta correspondencia: aunque la forma física del cuerpo no se modifica al pasar al plano de Laplace, las condiciones límite de tracción o desplazamiento pueden alterarse espacialmente en la transformación. Por ejemplo, si la tracción impuesta es\(\hat{T} = \cos (xt)\), entonces\(\bar{\hat{T}} = s/(s^2 + x^2)\); esto es obviamente de una forma espacial diferente a la original
función no transformada. Sin embargo, las funciones que se pueden escribir como factores separables de espacio y tiempo no cambiarán espacialmente en la transformación:
\(\hat{T} (x, t) = f(x) g(t) \Rightarrow \bar{\hat{T}} = f(x) \bar{g}(s)\)
Esto significa que los problemas de análisis de tensiones cuyas limitaciones de límite son independientes del tiempo o, en el peor de los casos, son funciones separables del espacio y el tiempo se verán iguales tanto en el plano real como en el plano de Laplace. En el plano de Laplace, el problema es entonces geométricamente idéntico a un problema elástico “asociado”.
Habiendo reducido el problema viscoelástico a uno elástico asociado al tomar transformaciones, se puede utilizar la vasta biblioteca de soluciones elásticas: se busca la solución al problema elástico asociado, y luego se realiza una inversión de Laplace para regresar al plano de tiempo. El proceso de análisis de esfuerzo viscoelástico empleando métodos de transformación suele denominarse “principio de correspondencia”, el cual se puede afirmar como la siguiente receta:
1. Determinar la naturaleza del problema elástico asociado. Si la distribución espacial de las condiciones límite y de fuerza corporal no cambia en la transformación, una ocurrencia común, entonces el problema elástico asociado aparece exactamente como el viscoelástico original.
2. Determinar la solución a este problema elástico asociado. Esto a menudo se puede hacer por referencia a manuales estándar (Por ejemplo, W.C. Young, Roark's Formulas for Stress and Strain, McGraw-Hill, Inc., Nueva York, 1989.) o textos sobre la teoría de la elasticidad (Por ejemplo, S. Timoshenko y J.N. Goodier, Theory of Elasticidad, McGraw-Hill, Inc., Nueva York, 1951.).
3. Refundir las constantes elásticas que aparecen en la solución elástica en términos de operadores viscoelásticos adecuados. Como se discute en la Sección 5.1, a menudo es conveniente reemplazar\(E\) y\(ν\) con\(G\) y\(K\), y luego reemplazar el\(G\) y\(K\) por sus análogos viscoelásticos:
\(\left \{ \begin{array} {c} E \\ v \end{array} \right \} \to \begin{cases} G \to \mathcal{G} \\ K \to \mathcal{K} \end{cases}\)
- Reemplace los límites aplicados y las restricciones de fuerza corporal por sus contrapartes transformadas:
\(\hat{T} \Rightarrow \bar{\hat{T}}\)
\(\hat{u} \Rightarrow \bar{\hat{u}}\)
donde\(\hat{T}\) y\(\hat{u}\) se imponen tracciones y desplazamientos, respectivamente.
5. Invertir la expresión así obtenida para obtener la solución al problema viscoelástico en el plano de tiempo.
Si la solución elástica contiene solo dos cantidades dependientes del tiempo en el numerador, como en la Ecuación 5.4.54, el principio de correspondencia es equivalente al método de superposición de la sección anterior. Usando el ejemplo de recipiente a presión, el método de correspondencia da
\(\delta_r = \dfrac{pr^2 C}{b} \to \bar{\delta}_r (s) = \dfrac{r^2}{b} \bar{p} \mathcal{C}\)
Ya que\(\mathcal{C} = s \bar{C}_{crp}\), la relación de transformación para integrales de convolución da
como antes. Sin embargo, el principio de correspondencia es más sencillo en problemas que tienen una complicada mezcla de funciones dependientes del tiempo, como se demuestra en el siguiente ejemplo.
Ejemplo\(\PageIndex{14}\)
La solución elástica para la expansión radial de un recipiente a presión cilíndrico de extremo cerrado de radio\(r\) y espesor\(b\) es
Siguiendo la receta del principio de correspondencia, la solución asociada en el plano de Laplace es
En términos de funciones hidrostáticas y de respuesta al cizallamiento, los operadores viscoelásticos son:
\(\mathcal{E} (s) = \dfrac{9\mathcal{G} (s) \mathcal{K} (s)}{3 \mathcal{K} (s) + \mathcal{G} (s)}\)
En Ejemplo\(\PageIndex{12}\), se consideró un material de PVC a 75\(^{\circ}C\) que a una buena aproximación era elástico en respuesta hidrostática y viscoelástico en cizallamiento. Usando el modelo sólido lineal estándar, tuvimos
\(\mathcal{K} = K_e, \ \ \ \mathcal{G} = G_r + \dfrac{(G_g - G_r)s}{s + \tfrac{1}{\tau}}\)
donde\(K_e =1.33\) GPa,\(G_g =800\) MPA,\(G_r =1.67\) MPa, y\(\tau =100\) s.
Para presión interna constante\(p(t) = p_0\),\(\bar{p} = p_0/s\). Todas estas expresiones deben ser combinadas, y el resultado invertido. Los comandos de Maple para este problema podrían ser:
define shear operator > G:=Gr+((Gg-Gr)*s)/(s+(1/tau)); define Poisson operator > N:=(3*K-2*G)/(6*K+2*G); define modulus operator > Eop:=(9*G*K)/(3*K+G); define pressure operator > pbar:=p0/s; get d1, radial displacement (in Laplace plane) > d1:=(pbar*r^2)*(1-(N/2))/(b*Eop); read Maple library for Laplace transforms > readlib(inttrans); invert transform to get d2, radial displacement in real plane > d2:=invlaplace(d1,s,t);
Después de algún reordenamiento manual, el desplazamiento radial se\(\delta_r(t)\) puede escribir en la forma
donde está el tiempo de retraso de fluencia\(\tau_c = \tau (G_g/G_r)\). Continuando con la sesión de Maple:
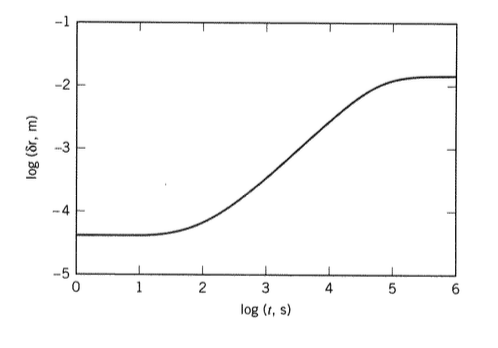
define numerical parameters > Gg:=800*10^6; Gr:=1.67*10^6; tau:=100; K:=1.33*10^9; > r:=.05; b:=.005; p0:=2*10^5; resulting expression for radial displacement > d2; - .01494 exp( - .00002088 t) + .01498
En la Figura 21 se muestra una gráfica log-log de esta función. Obsérvese que para este problema el efecto del pequeño cambio en la relación de Poisson\(ν\) durante la transición es despreciable en comparación con el cambio muy grande en el módulo\(E\), por lo que se habría obtenido un resultado casi idéntico simplemente dejando\(ν\) = constante = 0.5. Por otro lado, no es apreciablemente más difícil incluir la dependencia del tiempo de\(ν\) si el software de manipulación simbólica está disponible.
6. Referencias adicionales
- Aklonis, J.J., MackNight, W.J., y Shen, M., Introducción a la viscoelasticidad polimérica, Wiley-Interscience, Nueva York, 1972.
- Christensen, R.M., Teoría de la Viscoelasticidad, 2a ed., Academic Press, Nueva York, 1982.
- Ferry, J.D., Viscoelastic Properties of Polymers, 3a ed., Wiley & Sons, Nueva York, 1980.
- Flugge, W., Viscoelasticidad, Springer-Verlag, Nueva York, 1975.
- McCrum, N.G, Read, B.E., y Williams, G., Anelastic and Dielectric in Polymeric Solids, Wiley & Sons, Londres, 1967. Disponible en Dover Publications, Nueva York.
- Tschoegl, N.W., La teoría fenomenológica del comportamiento viscoelástico lineal, Springer- Verlag, Heidelberg, 1989.
- Tschoegl, N.W., “Dependencia del tiempo en las propiedades de los materiales: una visión general”, Mecánica de materiales dependientes del tiempo, Vol. 1, pp. 3—31, 1997.
- Williams, M.L., “Análisis estructural de materiales viscoelásticos”, Revista AIAA, p. 785, mayo de 1964.
Ejercicio\(\PageIndex{1}\)
Trazar las funciones\(e^{-t/\tau}\) y\(1 - e^{t/\tau}\) versus\(\log_10 t\) de\(t = 10^{-2}\) a\(t= 10^2\). Tener dos curvas en la parcela para cada función, una para\(\tau = 1\) y otra para\(\tau = 10\).
Ejercicio\(\PageIndex{2}\)
Determinar la energía de activación aparente en (\(E^{\dagger}\)en la Ecuación 5.4.2) para una relajación viscoelástica en la que se observa que la tasa inicial se duplica cuando la temperatura se incrementa de 20\(^{\circ} C\) a 30\(^{\circ} C\). (Respuesta:\(E^{\dagger} = 51\ kJ/mol\).)
Ejercicio\(\PageIndex{3}\)
Determinar la densidad de entrecruzamiento\(N\) y el peso molecular del segmento\(M_c\) entre los entrecruzamientos para un caucho con un módulo inicial\(E = 1000\) psi at\(20^{\circ}C\) y densidad\(1.1 \ g/cm^3\). (Respuesta:\(N = 944\ mol/m^3, M_c = 1165\ g/mol\).)
Ejercicio\(\PageIndex{4}\)
Expandir las formas exponenciales para la tensión dinámica y la deformación (\(\sigma (t) = \sigma_0^* e^{i\omega t}, \epsilon (t) =\epsilon_0^* e^{i\omega t}\)) y mostrar que
\(E^* = \dfrac{\sigma(t)}{\epsilon (t)} = \dfrac{\sigma_0 \cos \delta}{\epsilon_0} + i\dfrac{\sigma_0 \sin \delta}{\epsilon_0}\),
donde\(\delta\) está el ángulo de fase entre la tensión y la deformación.
Ejercicio\(\PageIndex{5}\)
Usando la relación\(\bar{\sigma} = \mathcal{E} \bar{\epsilon}\) para el caso de carga dinámica (\(\epsilon (t) = \epsilon_0 \cos \omega t\)) y respuesta material S.L.S.\(\left(\mathcal{E} = k_e + k_1s/(s + \tfrac{1}{\tau})\right)\), resolver para el estrés dependiente del tiempo\(\sigma (t)\). Utilice esta solución para identificar los componentes de estado estacionario del módulo\(E^* = E' + iE''\) complejo y también el componente transitorio. Respuesta:
Ejercicio\(\PageIndex{6}\)
Para el Sólido Lineal Estándar con parámetros\(k_e = 25\)\(k_1 = 50\),, y\(\tau_1 = 1\), plot\(E'\) y\(E''\) versus\(\log \omega\) en el rango\(10^{-2} < \omega \tau_1 < 10^2\). También graficar\(E''\) versus\(E'\) en este mismo rango, usando ejes ordinarios en lugar de logarítmicos y la misma escala para ambos ejes (diagrama Argand).
Ejercicio\(\PageIndex{7}\)
Demostrar que se puede escribir la ley viscoelástica para la forma “Voigt” del Sólido Lineal Estándar (un resorte de rigidez\(k_v = 1/C_v\) en paralelo con un amortiguador de viscosidad\(eta\), y esta combinación en serie con otro resorte de rigidez\(k_g = 1/C_g\))
\(\bar{\epsilon} = \mathcal{C} \bar{\sigma}, \text{ with } \mathcal{C} = \left [C_g + \dfrac{C_v}{\tau(s + \tfrac{1}{\tau})} \right ] \)
donde\(\tau = \eta /k_v\).
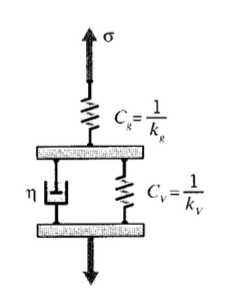
Ejercicio\(\PageIndex{8}\)
Demostrar que el cumplimiento de fluencia del modelo Voigt SLS de Ejercicio\(\PageIndex{7}\) es
Ejercicio\(\PageIndex{9}\)
En los casos en que se prescribe la tensión en lugar de la tensión, el modelo Kelvin, una disposición en serie de elementos Voigt, es preferible al modelo Wiechert:
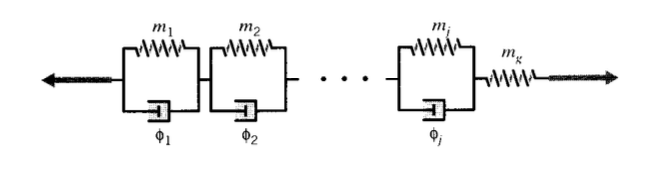
donde\(\phi_j = 1/\eta_j = \dot{\epsilon}_j/\sigma_{dj}\) y\(m_j = 1/k_j = \epsilon_j/\sigma_{sj}\) Usando las relaciones\(\epsilon = \epsilon_g + \sum_j \epsilon_j\),\(\sigma = \sigma_{sj} + \sigma_{dj}\),\(\tau_j = m_j /\phi_j\), muestran que la ecuación constitutiva viscoelástica asociada es:
\(\bar{\epsilon} = \left [m_g + \sum_j \dfrac{m_j}{\tau_j (s + \tfrac{1}{\tau_j})} \right ] \bar{\sigma}\)
y para este modelo mostrar el cumplimiento de fluencia para ser:
Ejercicio\(\PageIndex{10}\)
Para un modelo simple de Voigt (\(C_g = 0\)en Ejercicio\(\PageIndex{7}\)), mostrar que la tensión\(\epsilon^{t + \Delta t}\) en el momento se\(t + \Delta t\) puede escribir en términos de la tensión\(\epsilon^t\) en el momento\(t\) y el estrés\(\sigma^t\) que actúa durante el incremento de tiempo\(\Delta t\) como
Utilice este algoritmo para trazar la deformación por fluencia derivada de una tensión constante\(\sigma = 100\) versus\(\log t =(1, 5)\) for\(C_v = 0.05\) y\(\tau = 1000\).
Ejercicio\(\PageIndex{11}\)
Trazar la respuesta de deformación\(\epsilon (t)\) a una entrada de tensión de carga-descarga definida como
\(\sigma (t) = \begin{cases} 0, & t < 1 \\ 1, & 1 < t < 4.5 \\ -1, & 4.5 < t < 5 \\ 0, & t > 5 \end{cases}\)
El material obedece a la ley de cumplimiento de SLS (Ecuación 5.4.30) con\(C_g = 5, C_r = 10\), y\(\tau = 2\).
Ejercicio\(\PageIndex{12}\)
Usando la forma Maxwell del sólido lineal estándar con\(k_e = 10, k_1 = 100\) y\(\eta = 1000\):
a) Trazar\(E_{rel} (t)\) y\(E_{crp} (t) = 1/C_{crp} (t)\) versus tiempo logarítmico.
b) Parcela\([E_{crp}(t) - E_{rel}(t)]\) versus tiempo logarítmico.
c) Comparar el tiempo de relajación con el tiempo de retraso (el tiempo en que el argumento de lo exponencial se convierte en -1, para relajación y fluencia respectivamente). Especular sobre por qué uno es más corto que el otro.
Ejercicio\(\PageIndex{13}\)
Demostrar que un modelo Wiechert con dos brazos Maxwell (Ecuación 5.4.34) es equivalente a la ecuación diferencial ordinaria de segundo orden
\(a_2 \ddot{\sigma} + a_1 \dot{\sigma} + a_0 \sigma = b_2 \ddot{\epsilon} + b_1 \dot{\epsilon} + b_0 \epsilon\)
donde
\(a_2 = \tau_1 \tau_2, \ \ \ \ a_1 = \tau_1 + \tau_2, \ \ \ \ a_0 = 1\)
\(b_2 = \tau_1 \tau_2 (k_e + k_1 + k_2), \ \ \ \ b_1 = k_e (\tau_1 + \tau_2) + k_1 \tau_1 + k_2 \tau_2, \ \ \ \ b_0 = k_e\)
Ejercicio\(\PageIndex{14}\)
Para un material viscoelástico definido por la ecuación constitutiva diferencial:
\(15 \ddot{\sigma} + 8 \dot{\sigma} = \sigma = 105 \ddot{\epsilon} + 34 \dot{\epsilon} + \epsilon\),
escribir una expresión para el módulo de relajación en la forma de la serie PRONY (Ecuación 5.4.36). (Respuesta:\(E_{rel} = 1 + 2e^{-t/3} + 4e^{-t/5}\))
Ejercicio\(\PageIndex{15}\)
Para el simple elemento Maxwell, verifica que
Ejercicio\(\PageIndex{16}\)
Evaluar la integral de Boltzman
para determinar la respuesta del Sólido Lineal Estándar a la deformación sinusoidal\((\epsilon (t) = \cos (\omega t))\)
Ejercicio\(\PageIndex{17}\)
Derivar la Ecuación 5.4.48 mediante el uso de la expresión de Arrhenius para el tiempo de relajación para restar el tiempo de relajación logarítmica a una temperatura arbitraria\(T\) del tiempo de referencia\(T_{ref}\).
Ejercicio\(\PageIndex{18}\)
Usando datos de relajación de estrés isotérmico a diversas temperaturas, se han medido los factores de desplazamiento para un material de poliuretano como se muestra en la siguiente tabla:
| \(T, ^{\circ} C\) | \(\log_{10} a_T\) |
| +5 | -0.6 |
| 0 | 0 |
| -5 | 0.8 |
| -10 | 1.45 |
| -15 | 2.30 |
| -20 | 3.50 |
| -25 | 4.45 |
| -30 | 5.20 |
(a) Trazar\(\log a_T\) vs.\(1/T (^{\circ} K)\); computar una energía de activación promedio usando Eqn 5.4.48. (Respuesta:\(E^{\dagger} = 222 kJ/mol\).)
(b) Trazar\(\log a_T\) vs.\(T(^{\circ} C)\) y comparar con la ecuación WLF (Ecuación 5.4.50), con\(T_g = -35^{\circ} C\). (Tenga en cuenta que\(T_{ref} = 0 \ne T_g\).)
Ejercicio\(\PageIndex{19}\)
Después del cambio de tiempo-temperatura, una curva maestra de relajación a 0\(^{\circ} C\) para el poliuretano de Ejercicio\(\PageIndex{18}\) da los siguientes valores de\(E_{rel} (t)\) en varios momentos:
| \(\log (t, min)\) | \(E_{rel} (t)\), psi |
| -6 | 56,280 |
| -5 | 22,880 |
| -4 | 4,450 |
| -3 | 957 |
| -2 | 578 |
| -1 | 481 |
| 0 | 480 |
a) En la Ecuación 5.4.36, elija\(k_e = E_{rel} (t = 0) = 480\).
(b) Elegir valores de\(\tau_j\) para que coincidan con los tiempos dados en la tabla anterior de\(10^{-6}\) a\(10^{-1}\) (un proceso llamado “colocación”).
(c) Determinar los valores apropiados para las rigideces de resorte\(k_j\) correspondientes a cada una de\(\tau_j\) manera que la Ecuación 5.4.36 coincida con los valores experimentales de\(E_{rel} (t)\). Esto se puede hacer configurando y resolviendo una secuencia de ecuaciones algebraicas lineales con las incógnitas\(k_j\) como:
Tenga en cuenta que la matriz de coeficientes es esencialmente triangular, lo que facilita la solución manual en caso de que no se disponga de una computadora.
(d) Ajustar el valor de\(k_1\) para que la suma de todas las rigideces del muelle sea igual al módulo vítreo\(E_g = 91,100\) psi.
(e) Trazar el módulo de relajación predicho por el modelo de\(\log t = -8\) a 0.
Ejercicio\(\PageIndex{20}\)
Trazar los valores de relajación (deformación constante) del módulo\(E\) y la relación de Poisson\(ν\) para el poliisobutileno cuya respuesta dilatacional y de cizallamiento se muestra en la Figura 17. Asumir modelos S.L.S. tanto para dilatación como para cizallamiento.
Ejercicio\(\PageIndex{21}\)
La solución elástica para la tensión\(\sigma_x (x,y)\) y deflexión vertical\(v(x,y)\) en una viga en voladizo de longitud\(L\) y momento de inercia\(I\), cargada en el extremo libre con una fuerza\(F\), es
Determinar las contrapartes viscoelásticas de estas relaciones utilizando los métodos tanto de superposición como de correspondencia, asumiendo el comportamiento de S.L.S. para el cumplimiento del material (Ecuación 5.4.30).
Ejercicio\(\PageIndex{22}\)
Un polímero con propiedades viscoelásticas como se indica en la Figura 17 se coloca en una matriz circular rígida y se carga con una presión\(\sigma_y = 1\) MPa. Trazar la tensión transversal\(\sigma_x (t)\) y la tensión axial\(\epsilon_y (t)\) sobre\(\log t = -5\) 1. La solución elástica es