5.3: Análisis de elementos finitos
- Page ID
- 83326
Introducción
El análisis de elementos finitos (FEA) se ha convertido en algo común en los últimos años, y ahora es la base de una industria multimillonaria por año. Ahora se pueden obtener soluciones numéricas incluso a problemas de estrés muy complicados utilizando FEA de manera rutinaria, y el método es tan importante que incluso los tratamientos introductorios de Mecánica de Materiales, como estos módulos, deberían delinear sus principales características.
A pesar de la gran potencia de la FEA, las desventajas de las soluciones informáticas deben tenerse en cuenta al usar este y otros métodos similares: no necesariamente revelan cómo las tensiones son influenciadas por variables problemáticas importantes como las propiedades de los materiales y las características geométricas, y los errores en los datos de entrada pueden producir resultados tremendamente incorrectos que pueden ser pasados por alto por el analista. Quizás la función más importante del modelado teórico es la de afilar la intuición del diseñador; los usuarios de códigos de elementos finitos deben planificar su estrategia hacia este fin, complementando la simulación por computadora con el mayor análisis de forma cerrada y experimental posible.
Los códigos de elementos finitos son menos complicados que muchos de los paquetes de procesamiento de textos y hojas de cálculo que se encuentran en las microcomputadoras modernas. Sin embargo, son lo suficientemente complejos como para que la mayoría de los usuarios no encuentren efectivo programar su propio código. Se encuentran disponibles varios códigos comerciales preescritos, que representan un amplio rango de precios y son compatibles con máquinas desde microcomputadoras hasta supercomputadoras (C.A. Brebbia, ed., Finite Element Systems, A Handbook, Springer-Verlag, Berlín, 1982.). Sin embargo, los usuarios con necesidades especializadas no deben necesariamente rehuir el desarrollo de código, y pueden encontrar las fuentes de código disponibles en textos como el de Zienkiewicz (O.C. Zienkiewicz y R.L. Taylor, The Finite Element Method, McGraw-Hill Co., Londres, 1989.) como un punto de partida útil. La mayoría del software de elementos finitos está escrito en Fortran, pero algunos códigos más nuevos como el fieltro están en C u otros lenguajes de programación más modernos.
En la práctica, un análisis de elementos finitos suele consistir en tres etapas principales:
1. Preprocesamiento: El usuario construye un modelo de la pieza a analizar en el que la geometría se divide en una serie de subregiones discretas, o “elementos”, conectados en puntos discretos llamados “nodos”. Algunos de estos nodos tendrán desplazamientos fijos, y otros tendrán cargas prescritas. Estos modelos pueden llevar mucho tiempo de prepararse, y los códigos comerciales compitan entre sí para tener el “preprocesador” gráfico más fácil de usar para ayudar en esta tarea bastante tediosa. Algunos de estos preprocesadores pueden superponer una malla en un archivo CAD preexistente, de modo que el análisis de elementos finitos se puede realizar convenientemente como parte del proceso computarizado de redacción y diseño.
2. Análisis: El conjunto de datos preparado por el preprocesador se utiliza como entrada al propio código de elementos finitos, el cual construye y resuelve un sistema de ecuaciones algebraicas lineales o no lineales
\(K_{ij} u_j = f_i\)
donde\(u\) y\(f\) son los desplazamientos y fuerzas aplicadas externamente en los puntos nodales. La formación de la\(K\) matriz depende del tipo de problema que se esté atacando, y este módulo esbozará el enfoque para los análisis de truss y esfuerzos elásticos lineales. Los códigos comerciales pueden tener bibliotecas de elementos muy grandes, con elementos apropiados para una amplia gama de tipos de problemas. Una de las principales ventajas de FEA es que muchos tipos de problemas se pueden abordar con el mismo código, simplemente especificando los tipos de elementos apropiados de la biblioteca.
3. Postprocesamiento: En los primeros días del análisis de elementos finitos, el usuario poro a través de resmas de números generados por el código, enumerando desplazamientos y tensiones en posiciones discretas dentro del modelo. Es fácil pasar por alto tendencias importantes y puntos calientes de esta manera, y los códigos modernos utilizan pantallas gráficas para ayudar a visualizar los resultados. Una pantalla típica del postprocesador superpone contornos de colores que representan los niveles de tensión en el modelo, mostrando una imagen de campo completo similar a la de los resultados experimentales fotoelásticos o muaré
El funcionamiento de un código específico generalmente se detalla en la documentación que acompaña al software, y los proveedores de los códigos más caros suelen ofrecer talleres o sesiones de capacitación para ayudar a los usuarios a aprender las complejidades de la operación del código. Un problema que los usuarios pueden tener incluso después de esta capacitación es que el código tiende a ser una “caja negra” cuyo funcionamiento interno no se entiende. En este módulo describiremos los principios que subyacen a la mayoría de los códigos actuales de análisis de esfuerzos por elementos finitos, limitando la discusión al análisis elástico lineal por ahora. Comprender esta teoría ayuda a disipar el síndrome de caja negra, y también sirve para resumir los fundamentos analíticos de la mecánica sólida.
Análisis matricial de cerchas
Las cerchas articuladas con pasador, discutidas más a fondo en el Módulo 5, proporcionan una buena manera de introducir los conceptos de FEA. El análisis estático de las cerchas se puede llevar a cabo exactamente, y las ecuaciones de armaduras incluso complicadas se pueden ensamblar en forma de matriz susceptible de solución numérica. Este enfoque, a veces llamado “análisis matricial”, proporcionó la base del desarrollo temprano de FEA.
El análisis matricial de las cerchas opera considerando la rigidez de cada elemento de celosía uno a la vez, y luego usando estas rigideces para determinar las fuerzas que se configuran en los elementos de celosía por los desplazamientos de las juntas, generalmente llamadas “nodos” en el análisis de elementos finitos. Después al señalar que la suma de las fuerzas aportadas por cada elemento a un nodo debe ser igual a la fuerza que se aplica externamente a ese nodo, podemos ensamblar una secuencia de ecuaciones algebraicas lineales en las que los desplazamientos nodales son las incógnitas y las fuerzas nodales aplicadas son cantidades conocidas. Estas ecuaciones están convenientemente escritas en forma de matriz, lo que le da nombre al método:
\(\begin{bmatrix} K_{11} & K_{12} & \cdots & K_{1n} \\ K_{21} & K_{22} & \cdots & K_{2n} \\ \cdots & \cdots & \cdots & \cdots \\ K_{n1} & K_{n2} & \cdots & K_{nn} \end{bmatrix} \left \{ \begin{array} {c} u_1 \\ u_2 \\ \cdots \\ u_n \end{array} \right \} = \left \{ \begin{array} {c} f_1 \\ f_2 \\ \cdots \\ f_n \end{array} \right \}\)
Aquí\(u_i\) e\(f_j\) indicar la desviación en el nodo i-ésimo y la fuerza en el\(j^{th}\) nodo (estas serían en realidad cantidades vectoriales, con subcomponentes a lo largo de cada eje de coordenadas). La matriz de\(K_{ij}\) coeficientes se denomina matriz de rigidez global, siendo el\(ij\) componente físicamente la influencia del\(j^{th}\) desplazamiento sobre la\(i^{th}\) fuerza. Las ecuaciones matriciales se pueden abreviar como
\[K_{ij} u_j = f_i \text{ or } Ku = f\]
usando subíndices o negritas para indicar cantidades de vectores y matrices.
Ya sea la fuerza aplicada externamente o el desplazamiento se conoce al principio para cada nodo, y es imposible especificar simultáneamente tanto un desplazamiento arbitrario como una fuerza sobre un nodo dado. Estas fuerzas nodales prescritas y desplazamientos son las condiciones límite del problema. Es tarea de análisis determinar las fuerzas que acompañan a los desplazamientos impuestos, y los desplazamientos en los nodos donde se aplican fuerzas externas conocidas.
Matriz de rigidez para un solo elemento de celosía
Como primer paso en el desarrollo de un conjunto de ecuaciones matriciales que describan los sistemas de celosía, necesitamos una relación entre las fuerzas y los desplazamientos en cada extremo de un solo elemento de celosía. Considera tal elemento en el\(x - y\) plano como se muestra en la Figura 1, unido a nodos numerados\(i\)\(j\) e inclinados en ángulo con respecto\(\theta\) a la horizontal.
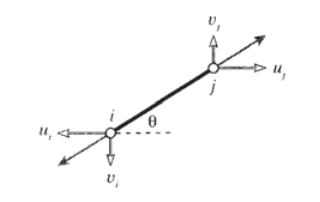
Considerando el vector de elongación\(\delta\) a resolver en direcciones a lo largo y transversal al elemento, el alargamiento en el elemento de celosía se puede escribir en términos de las diferencias en los desplazamientos de sus puntos finales:
donde\(u\) y\(v\) son los componentes horizontal y vertical de las deflexiones, respectivamente. (Los desplazamientos en el nodo\(i\) dibujado en la Figura 1 son negativos.) Esta relación se puede escribir en forma de matriz como:
\(\delta = \begin{bmatrix} -c & -s & c & s \end{bmatrix} \left \{ \begin{array} {c} u_i \\ v_i \\ u_j \\ v_j \end{array} \right \}\)
Aquí\(c = \cos \theta\) y\(s = \sin \theta\).
La fuerza axial\(P\) que acompaña al alargamiento\(\delta\) viene dada por la ley de Hooke para cuerpos elásticos lineales como\(P = (AE/L) \delta\). Las fuerzas nodales horizontales y verticales se muestran en la Figura 2; estas pueden escribirse en términos de la fuerza axial total como:
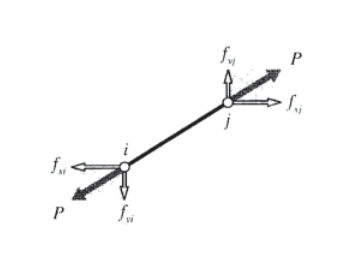
\(\left \{ \begin{array} {c} f_{xi} \\ f_{yi} \\ f_{xj} \\ f_{yj} \end{array} \right \} = \left \{ \begin{array} {c} -c \\ -s \\ c \\ s \end{array} \right \} P = \left \{ \begin{array} {c} -c \\ -s \\ c \\ s \end{array} \right \} \dfrac{AE}{L} \delta\)
\(= \left \{ \begin{array} {c} -c \\ -s \\ c \\ s \end{array} \right \} \dfrac{AE}{L} \begin{bmatrix} -c & -s & c & s \end{bmatrix} \left \{ \begin{array} {c} u_i \\ v_i \\ u_j \\ v_j \end{array} \right \}\)
Realización de la multiplicación matricial:
\[\left \{ \begin{array} {c} f_{xi} \\ f_{yi} \\ f_{xj} \\ f_{yj} \end{array} \right \} = \dfrac{AE}{L} \begin{bmatrix} c^2 & cs & -c^2 & -cs \\ cs & s^2 & -cs & -s^2 \\ -c^2 & -cs & c^2 & cs \\ -cs & -s^2 & cs & s^2 \end{bmatrix} \left \{ \begin{array} {c} u_i \\ v_i \\ u_j \\ v_j \end{array} \right \}\]
La cantidad entre paréntesis, multiplicada por\(AE/L\), se conoce como la “matriz de rigidez del elemento”\(k_{ij}\). Cada uno de sus términos tiene un significado físico, representando la contribución de uno de los desplazamientos a una de las fuerzas. El sistema global de ecuaciones se forma combinando las matrices de rigidez de elementos de cada elemento de celosía a su vez, por lo que su cálculo es central para el método de análisis estructural matricial. La principal diferencia entre el método de celosía matricial y el método general de elementos finitos radica en cómo se forman las matrices de rigidez de elementos; la mayoría de las otras operaciones informáticas son las mismas.
Ensamblaje de contribuciones de múltiples elementos
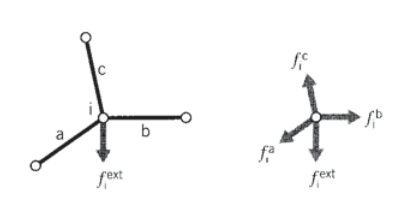
El siguiente paso es considerar un ensamblaje de muchos elementos de celosía conectados por uniones de pasador. Cada elemento que se reúne en una articulación, o nodo, aportará allí una fuerza según lo dictado por los desplazamientos de ambos nodos de ese elemento (ver Figura 3). Para mantener el equilibrio estático, todas las contribuciones de fuerza de elemento\(f_{i}^{elem}\) en un nodo dado deben sumarse a la fuerza\(f_i^{ext}\) que se aplica externamente en ese nodo:
\(f_i^{ext} = \sum_{elem} f_i^{elem} = (\sum_{elem} k_{ij}^{elem} u_j) = (\sum_{elem} k_{ij}^{elem}) u_j = K_{ij} u_j\)
Cada matriz de rigidez de elemento\(k_{ij}^{elem}\) se agrega a la ubicación apropiada de la matriz de rigidez global o “global”\(K_{ij}\) que relaciona todos los desplazamientos y fuerzas de la armadura. Este proceso se llama “montaje”. Los números de índice en la relación anterior deben ser los números “globales” asignados a la estructura de celosía en su conjunto. Sin embargo, generalmente es conveniente calcular las matrices de rigidez de elementos individuales usando un esquema local, y luego hacer que la computadora convierta a números globales al ensamblar las matrices individuales.
Ejemplo\(\PageIndex{1}\)
El proceso de ensamblaje está en el corazón del método de elementos finitos, y vale la pena hacer un simple caso a mano para ver cómo funciona realmente. Consideremos el problema del truss de dos elementos de la Figura 4, asignándose a los nodos números arbitrarios “globales” del 1 al 3. Dado que cada nodo puede moverse en general en dos direcciones, hay grados\(3 \times 2 = 6\) totales de libertad en el problema. La matriz de rigidez global será entonces una\(6 \times 6\) matriz que relaciona los seis desplazamientos con las seis fuerzas aplicadas externamente. Solo se desconoce uno de los desplazamientos en este caso, ya que todos menos el desplazamiento vertical del nodo 2 (grado de libertad número 4) está restringido a ser cero. La Figura 4 muestra una lista viable de los números globales, y también números “locales” para cada elemento individual.
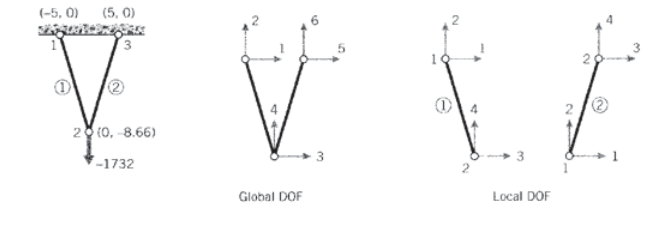
Utilizando los números locales, la matriz de rigidez del\(4 \times 4\) elemento de cada uno de los dos elementos puede evaluarse de acuerdo con la Ecuación 5.3.2. El ángulo de inclinación se calcula a partir de las coordenadas nodales como
La matriz resultante para el elemento 1 es:
\(k^{(1)} = \begin{bmatrix} 25.00 & -43.30 & -25.00 & 43.30 \\ -43.30 & 75.00 & 43.30 & -75.00 \\ -25.00 & 43.30 & 25.00 & -43.30 \\ 43.30 & -75.00 & -43.30 & 75.00 \end{bmatrix} \times 10^3\)
y para el elemento 2:
\(k^{(2)} = \begin{bmatrix} 25.00 & 43.30 & -25.00 & -43.30 \\ 43.30 & 75.00 & -43.30 & -75.00 \\ -25.00 & -43.30 & 25.00 & 43.30 \\ -43.30 & -75.00 & 43.30 & 75.00 \end{bmatrix} \times 10^3\)
(Es importante que las unidades sean consistentes; aquí las longitudes están en pulgadas, las fuerzas en libras y los módulos en psi. El módulo de ambos elementos es\(E = 10\) Mpsi y ambos tienen área\(A = 0.1 in^2\).) Estas matrices tienen filas y columnas numeradas del 1 al 4, correspondientes a los grados locales de libertad del elemento.
Sin embargo, cada uno de los grados locales de libertad puede ser igualado a uno de los grados globales del problema general. Por inspección de la Figura 4, podemos formar la siguiente tabla que mapea números locales a globales:
| local | global, elemento 1 | global, elemento 2 |
| 1 | 1 | 3 |
| 2 | 2 | 4 |
| 3 | 3 | 5 |
| 4 | 4 | 6 |
Usando esta tabla, vemos por ejemplo que el segundo grado de libertad para el elemento 2 es el cuarto grado de libertad en el sistema de numeración global, y el tercer grado local de libertad corresponde al quinto grado global de libertad. De ahí que el valor en la segunda fila y tercera columna de la matriz de rigidez del elemento 2, denotado\(k_{23}^{(2)}\), debe agregarse a la posición en la cuarta fila y quinta columna de la matriz de rigidez\(6 \times 6\) global. Escribimos esto como
\(k_{23}^{(2)} \to K_{4,5}\)
Cada una de las dieciséis posiciones en la matriz de rigidez de cada uno de los dos elementos debe agregarse a la matriz global de acuerdo con el mapeo dado por la tabla. Esto da el resultado
\(K = \begin{bmatrix} k_{11}^{(1)} & k_{12}^{(1)} & k_{13}^{(1)} & k_{14}^{(1)} & 0 & 0 \\ k_{21}^{(1)} & k_{22}^{(1)} & k_{23}^{(1)} & k_{24}^{(1)} & 0 & 0 \\ k_{31}^{(1)} & k_{32}^{(1)} & k_{33}^{(1)} + k_{11}^{(2)} & k_{34}^{(1)} + k_{12}^{(2)} & k_{13}^{(2)} & k_{14}^{(2)} \\ k_{41}^{(1)} & k_{42}^{(1)} & k_{43}^{(1)} + k_{21}^{(2)} & k_{44}^{(1)} + k_{22}^{(2)} & k_{23}^{(2)} & k_{24}^{(2)} \\ 0 & 0 & k_{31}^{(2)} & k_{32}^{(2)} & k_{33}^{(2)} & k_{34}^{(2)} \\ 0 & 0 & k_{41}^{(2)} & k_{42}^{(2)} & k_{43}^{(2)} & k_{44}^{(2)} \end{bmatrix}\)
Esta matriz premultiplica el vector de desplazamientos nodales de acuerdo con la Ecuación 5.3.1 para producir el vector de fuerzas nodales aplicadas externamente. Las ecuaciones del sistema completo, teniendo en cuenta las fuerzas y desplazamientos conocidos, son entonces
Obsérvese que ya sea se conoce la fuerza o el desplazamiento por cada grado de libertad, siendo desconocido el desplazamiento o fuerza que lo acompaña. Aquí solo se desconoce uno de los desplazamientos (\(u_4\)), pero en la mayoría de los problemas los desplazamientos desconocidos superan con creces en número a las fuerzas desconocidas. Tenga en cuenta también que solo aquellos elementos que están físicamente conectados a un nodo dado pueden aportar una fuerza a ese nodo. En la mayoría de los casos, esto da como resultado que la matriz de rigidez global contenga muchos ceros correspondientes a pares nodales que no están abarcados por un elemento. Las implementaciones efectivas de computadoras aprovecharán la dispersión de la matriz para conservar la memoria y reducir el tiempo de ejecución.
En problemas mayores las ecuaciones matriciales se resuelven para los desplazamientos y fuerzas desconocidos por reducción gaussiana u otras técnicas. En este problema de dos elementos, la solución para el único desplazamiento desconocido se puede anotar casi a partir de la inspección. Multiplicando la cuarta fila del sistema, tenemos
\(0 + 0 + 0 + 150 \times 10^3 u_4 + 0 + 0 = -1732\)
\(u_4 = -1732/150 \times 10^3 = -0.01155 in\)
Ahora cualquiera de las fuerzas desconocidas se puede obtener directamente. Multiplicar la primera fila, por ejemplo, da
\(0 + 0 + 0 + (43.4) (-0.0115) \times 10^3 + 0 + 0 = f_1\)
El signo negativo aquí indica que la fuerza horizontal en el nodo global #1 está a la izquierda, opuesta a la dirección asumida en la Figura 4.
El proceso de ciclar a través de cada elemento para formar la matriz de rigidez del elemento, ensamblar la matriz de elementos en las posiciones correctas en la matriz global, resolver las ecuaciones para desplazamientos y luego retromultiplicar para calcular las fuerzas, e imprimir los resultados puede automatizarse para hacer una muy código de computadora versátil.
El análisis de elementos finitos a mayor escala (y otros) se realiza mejor con un código informático dedicado, y uno excelente para aprender el método está disponible en la web en http://felt.sourceforge.net/. Este código, llamado felt, fue escrito por Jason Gobat y Darren Atkinson para uso educativo, e incorpora una serie de características novedosas para promover la facilidad de uso. La información completa que describe este código, así como la fuente en lenguaje C y una serie de ejecuciones de prueba y módulos de código auxiliar están disponibles a través de sus páginas web. Si tiene acceso a estaciones de trabajo X-window, también está disponible un shell gráfico llamado velvet.
Ejemplo\(\PageIndex{2}\)
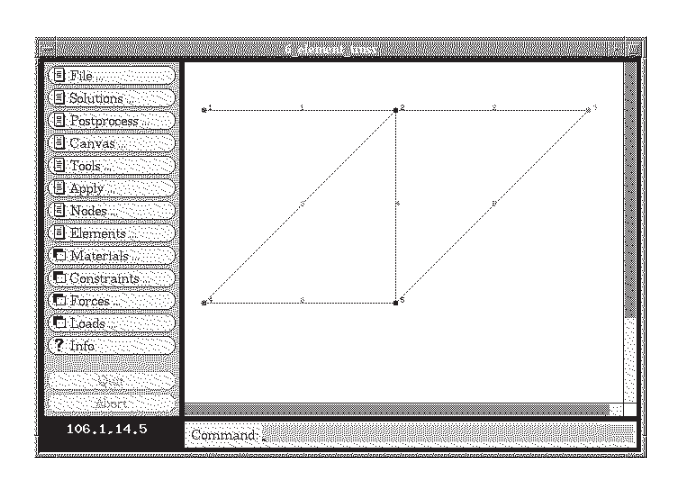
Para ilustrar cómo opera este código para un problema algo mayor, considere la armadura de seis elementos de la Figura 5, la cual fue analizada en el Módulo 5 tanto por el enfoque de análisis de cuerpo libre conjunto a la vez como por el método de Castigliano.
El conjunto de datos de entrada, que puede escribirse manualmente o desarrollarse gráficamente en terciopelo, emplea técnicas de análisis para simplificar lo que puede ser un paso muy tedioso y propenso a errores en el análisis de elementos finitos. El conjunto de datos para esta celosía de 6 elementos es:
problem description nodes=5 elements=6 nodes 1 x=0 y=100 z=0 constraint=pin 2 x=100 y=100 z=0 constraint=planar 3 x=200 y=100 z=0 force=P 4 x=0 y=0 z=0 constraint=pin 5 x=100 y=0 z=0 constraint=planar truss elements 1 nodes=[1,2] 2 nodes=[2,3] 3 nodes=[4,2] 4 nodes=[2,5] 5 nodes=[5,3] 6 nodes=[4,5] material=steel material properties steel E=3e+07 A=0.5 distributed loads constraints free Tx=u Ty=u Tz=u Rx=u Ry=u Rz=u pin Tx=c Ty=c Tz=c Rx=u Ry=u Rz=u planar Tx=u Ty=u Tz=c Rx=u Ry=u Rz=u forces P Fy=-1000 end
El significado de estas líneas debe ser bastante evidente en la inspección, aunque la documentación sentida debe ser consultada para mayor detalle. La salida producida por el fieltro para estos datos es:
** **
Desplazamientos Nodales
| Nodo # | DOF | DOF 2 | DOF 3 | DOF 4 | DOF 5 | DOF 6 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0.013333 | -0.03219 | 0 | 0 | 0 | 0 |
| 3 | 0.02 | -0.084379 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | -0.0066667 | -0.038856 | 0 | 0 | 0 | 0 |
Tensiones en los elementos
| 1: | 4000 |
| 2: | 2000 |
| 3: | -2828.4 |
| 4: | 2000 |
| 5: | -2828.4 |
| 6: | -2000 |
Fuerzas de Reacción
| Nodo # | DOF | Fuerza de reacción |
| 1 | Tx | -2000 |
| 1 | Ty | 0 |
| 1 | Tz | 0 |
| 2 | Tz | 0 |
| 3 | Tz | 0 |
| 4 | Tx | 2000 |
| 4 | Ty | 1000 |
| 4 | Tz | 0 |
| 5 | Tz | 0 |
Resumen de uso de materiales
Material: acero
Número: 6
Largo: 682.8427
Masa: 0.0000
Masa total: 0.0000
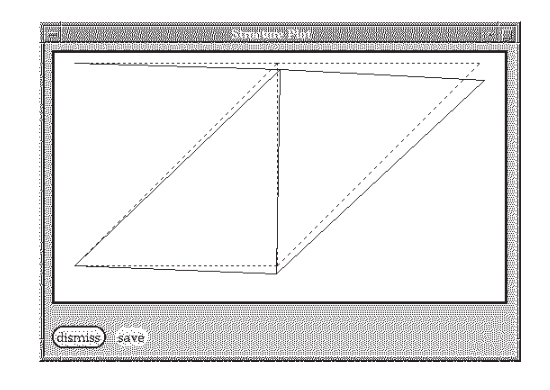
El desplazamiento vertical del nodo 3 (el valor DOF 2) es -0.0844, el mismo valor obtenido por los métodos de forma cerrada del Módulo 5. La Figura 6 muestra la salida gráfica de terciopelo para las deflexiones del truss (muy ampliadas).
Análisis General de Estrés
La matriz de rigidez del elemento podría formarse exactamente para elementos de celosía, pero este no es el caso para situaciones generales de análisis de tensión. La relación entre las fuerzas nodales y los desplazamientos no se conoce de antemano para problemas generales de análisis de esfuerzos bidimensionales o tridimensionales, y se debe utilizar una relación aproximada para escribir una matriz de rigidez de elementos.
En la habitual “formulación de desplazamiento” del método de elementos finitos, las ecuaciones gobernantes se combinan para que solo aparezcan desplazamientos como incógnitas; esto se puede hacer usando las ecuaciones constitutivas de Hookean para reemplazar las tensiones en las ecuaciones de equilibrio por las cepas, y luego usando el ecuaciones cinemáticas para sustituir las deformaciones por los desplazamientos. Esto da
\[L^T \sigma = L^T D_{\epsilon} = L^T DLu = 0\]
Por supuesto, muchas veces es imposible resolver estas ecuaciones en forma cerrada por las condiciones de encuadernación irregular que se encuentran en los problemas prácticos. Sin embargo, las ecuaciones son susceptibles de discretización y solución mediante técnicas numéricas como diferencias finitas o elementos finitos.
Los métodos de elementos finitos son una de varias técnicas numéricas aproximadas disponibles para la solución de problemas de valor límite de ingeniería. Los problemas en la mecánica de los materiales a menudo conducen a ecuaciones de este tipo, y los métodos de elementos finitos tienen una serie de ventajas en su manejo. El método es particularmente adecuado para problemas con geometrías irregulares y condiciones de contorno, y se puede implementar en códigos informáticos generales que pueden usarse para muchos problemas diferentes.
Para obtener una solución numérica para el problema del análisis de tensiones, postulemos una función\(\tilde{u} (x, y)\) como aproximación a\(u\):
\[\tilde{u} (x, y) \approx u (x, y)\]
Se podrían adoptar muchas formas diferentes para la aproximación\(\tilde{u}\). El método de elementos finitos discretiza el dominio de solución en un conjunto de subregiones, o “elementos”, cada uno de los cuales tiene sus propias funciones de aproximación. Específicamente, la aproximación para el desplazamiento\(\tilde{u} (x, y)\) dentro de un elemento se escribe como una combinación de los desplazamientos (aún desconocidos) en los nodos que pertenecen a ese elemento:
\[\tilde{u} (x, y) = N_j (x, y) u_j\]
Aquí los\(j\) rangos de índice sobre los nodos del elemento,\(u_j\) son los desplazamientos nodales, y las\(N_j\) son “funciones de interpolación”. Estas funciones de interpolación suelen ser polinomios simples (generalmente lineales, cuadráticos u ocasionalmente polinomios cúbicos) que se eligen para convertirse en unidad en el nodo\(j\) y cero en los nodos de otros elementos. Las funciones de interpolación pueden ser evaluadas en cualquier posición dentro del elemento por medio de subrutinas estándar, por lo que el desplazamiento aproximado en cualquier posición dentro del elemento se puede obtener en términos de los desplazamientos nodales directamente a partir de la Ecuación 5.3.5.
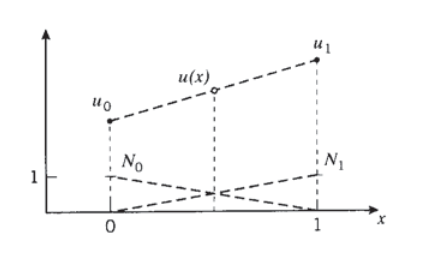
El concepto de interpolación se puede ilustrar preguntando cómo podríamos adivinar el valor de una función\(u(x)\) en un punto arbitrario\(x\) ubicado entre dos nodos en\(x = 0\) y\(x = 1\), suponiendo que conocemos de alguna manera los valores nodales\(u(0)\) y u (1). Podríamos suponer que como una aproximación razonable\(u(x)\) simplemente varía linealmente entre estos dos valores como se muestra en la Figura 7, y escribir
Aquí las\(N_0\) y\(N_1\) son las funciones de interpolación lineal para esta aproximación unidimensional. Los códigos de elementos finitos tienen subrutinas que extienden este concepto de interpolación a dos y tres dimensiones.
Las aproximaciones para la deformación y la tensión siguen directamente de los desplazamientos:
\[\tilde{\epsilon} L\tilde{u} = LN_ju_j \equiv B_j u_j\]
\[\tilde{\sigma} D \tilde{\epsilon} = DB_j u_j\]
donde\(B_j(x, y) = LN_j (x, y)\) es una matriz de derivadas de las funciones de interpolación:
\[B_j = \begin{bmatrix} N_{j,x} & 0 \\ 0 & N_{j, y} \\ N_{j, y} & N_{j, x} \end{bmatrix}\]
Ahora se puede invocar un argumento de “trabajo virtual” para relacionar el desplazamiento nodal\(u_j\) que aparece en el nodo\(j\) con las fuerzas aplicadas externamente en el nodo\(i\): si un desplazamiento pequeño o “virtual”\(\delta u_i\) se superpone sobre el nodo\(i\), el aumento de la energía de deformación\(\delta U\) dentro de un elemento conectado a ese nodo viene dado por:
\[\delta U = \int_V \delta \epsilon^T \sigma dV\]
donde\(V\) está el volumen del elemento. Utilizando la deformación aproximada obtenida de los desplazamientos interpolados,\(\delta \tilde{\epsilon} = B_i \delta u_i\) es el aumento virtual aproximado de la deformación inducido por el desplazamiento ganglionar virtual. Usando la Ecuación 5.3.7 y la identidad matricial\((AB)^T = B^T A^T\), tenemos:
\[\delta U = \delta u_i^T \int_V B_i^T DB_j dV u_j\]
(Los desplazamientos nodales\(\delta u_i^T\) y no\(u_j\) son funciones de\(x\) y\(y\), y así se pueden traer desde el interior de la integral.) El incremento en la energía de deformación\(\delta U\) debe ser igual al trabajo realizado por las fuerzas nodales; esto es:
\[\delta W = \delta u_i^T f_i\]
Equiparando Eqns. 5.3.10 y 5.3.11 y cancelando el factor común\(\delta u_i^T\), tenemos
\[[\int_V B_i^T DB_j dV] u_j = f_i\]
Esto es de la forma desired\(k_{ij} u_j = f_i\), donde\(k_{ij} = \int_V B_i^T DB_j dV\) está la rigidez del elemento.
Finalmente, la integral en la Ecuación 12 debe ser reemplazada por un equivalente numérico aceptable para la computadora. La integración numérica de Gauss-Legendre se usa comúnmente en códigos de elementos finitos para este propósito, ya que esa técnica proporciona una alta relación de precisión al esfuerzo de computación. Dicho brevemente, la integración consiste en evaluar el integrando en puntos de integración óptimamente seleccionados dentro del elemento, y formar una suma ponderada de los valores del integrando en estos puntos. En el caso de la integración sobre áreas de elementos bidimensionales, esto puede escribirse:
\[\int_A f(x, y) dA \approx \sum_l f(x_l, y_l) w_l\]
La ubicación de los puntos de muestreo\(x_l,y_l\) y los pesos asociados wl son proporcionados por subrutinas estándar. En la mayoría de los códigos modernos, estas rutinas mapean el elemento en una forma conveniente, determinan los puntos de integración y pesos en el marco de coordenadas transformado y luego mapean los resultados de nuevo al marco original. Las funciones Nj utilizadas anteriormente para la interpolación también pueden ser utilizadas para el mapeo, logrando una economía significativa en la codificación. Esto produce lo que se conoce como “elementos isoparamétricos numéricamente integrados”, y estos son un pilar de la industria de elementos finitos.
La Ecuación 5.3.12, con la integral reemplazada por integraciones numéricas de la forma en la Ecuación 5.3.13, es la contraparte de elemento finito de la Ecuación 5.3.3, la ecuación gobernante diferencial. La computadora llevará a cabo el análisis haciendo un lazo sobre cada elemento, y dentro de cada elemento haciendo un lazo sobre los puntos de integración individuales. En cada punto de integración los componentes de la matriz de rigidez del elemento\(k_{ij}\) se computan de acuerdo con la Ecuación 5.3.12, y se agregan a las posiciones apropiadas de la matriz de rigidez\(K_{ij}\) global como se hizo en la etapa de ensamblaje del método de celosía de matriz descrito en la sección anterior. Se puede apreciar que una buena cantidad de computación está involucrada solo en la formación de los términos de la matriz de rigidez, y que el método de elementos finitos nunca podría haberse desarrollado sin un acceso conveniente y económico a una computadora.
Tensiones alrededor de un orificio circular
Se ha considerado el problema de una placa cargada uniaxialmente que contiene un orificio circular en módulos anteriores, incluyendo la solución teórica de Kirsch (Módulo 16) y determinaciones experimentales mediante métodos fotoelásticos y muaré (Módulo 17). Este problema es de importancia práctica —por ejemplo, hemos notado la peligrosa concentración de esfuerzos que aparece cerca de los agujeros de los remaches— y también es bastante exigente tanto en análisis teóricos como numéricos. Dado que las tensiones aumentan bruscamente cerca del agujero, se debe refinar allí una rejilla de elementos finitos para producir resultados aceptables.
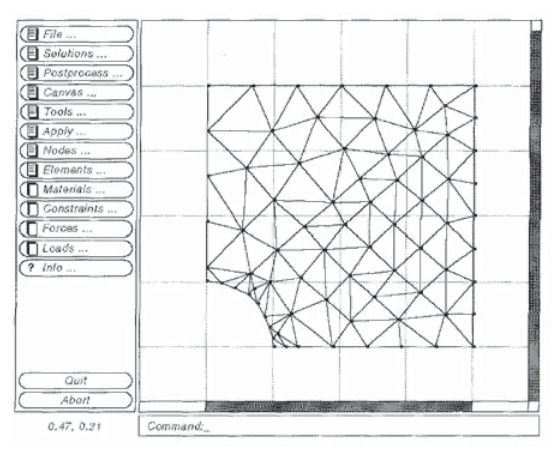
La Figura 8 muestra una malla de elementos triangulares de tres nudos desarrollados por el paquete gráfico de FEA de fieltro-terciopelo que se puede utilizar para aproximar los desplazamientos y tensiones alrededor de una placa cargada uniaxialmente que contiene un orificio circular. Dado que los resultados tanto teóricos como experimentales para este campo de tensión están disponibles como se mencionó anteriormente, el problema del agujero circular es bueno para familiarizarse con el funcionamiento del código.
El usuario debe aprovechar la simetría para reducir el tamaño del problema siempre que sea posible, y en este caso solo se necesita engranar un cuadrante del problema. El centro del agujero se mantiene fijo, por lo que la simetría requiere que los nodos a lo largo del borde izquierdo puedan moverse verticalmente pero no horizontalmente. De manera similar, los nodos a lo largo del borde inferior están restringidos verticalmente pero se dejan libres para moverse horizontalmente. Las cargas se aplican a los nodos a lo largo del borde superior, siendo cada carga la resultante de la tensión de campo lejano que actúa a lo largo de la mitad de los límites del elemento entre el nodo dado y sus vecinos. (El estrés de campo lejano se toma como unidad.) Porciones del conjunto de datos de entrada de fieltro para este problema son:
problem description nodes=76 elements=116 nodes 1 x=1 y=-0 z=0 constraint=slide_x 2 x=1.19644 y=-0 z=0 3 x=0.984562 y=0.167939 z=0 constraint=free 4 x=0.940634 y=0.335841 z=0 5 x=1.07888 y=0.235833 z=0 . . . 72 x=3.99602 y=3.01892 z=0 73 x=3.99602 y=3.51942 z=0 74 x=3.33267 y=4 z=0 75 x=3.57706 y=3.65664 z=0 76 x=4 y=4 z=0 CSTPlaneStress elements 1 nodes=[13,12,23] 2 nodes=[67,58,55] 6 nodes=[50,41,40] . . . 7 nodes=[68,67,69] 8 nodes=[68,58,67] 9 nodes=[57,58,68] 10 nodes=[57,51,58] 11 nodes=[52,51,57] 12 nodes=[37,39,52] 13 nodes=[39,51,52] . . . 116 nodes=[2,3,1] material properties steel E=2.05e+11 nu=0.33 t=1 distributed loads load_case_1 color=red direction=GlobalY values=(1,1) (3,1) constraints free Tx=u Ty=u Tz=u Rx=u Ry=u Rz=u slide_x color=red Tx=u Ty=c Tz=c Rx=u Ry=u Rz=u slide_y color=red Tx=c Ty=u Tz=c Rx=u Ry=u Rz=u end
Los\(y\) desplazamientos y tensiones verticales σy están contorneados en la Figura 9 (a) y (b) respectivamente; estos deben compararse con los análisis fotoelásticos y muaré dados en el Módulo 17, Figuras 8 y 10 (a). La tensión en el punto de integración más cercano al eje x en el agujero se calcula para ser\(\sigma_{y, \max} = 3.26\), 9% mayor que el valor teórico de 3.00. Al dibujar los contornos de la Figura 9b, el postprocesador extrapoló las tensiones a los nodos ajustando un plano de mínimos cuadrados a través de las tensiones en los cuatro puntos de integración dentro del elemento. Esto produce un valor aún mayor para el factor de concentración de esfuerzos, 3.593. El usuario debe ser consciente de que los postprocesadores gráficos suavizan los resultados que en sí mismos son solo aproximaciones, por lo que la inexactitud numérica es una posibilidad real. Refinar la malla, especialmente cerca de la región de mayor gradiente de tensión en el meridiano del agujero, reduciría este error.
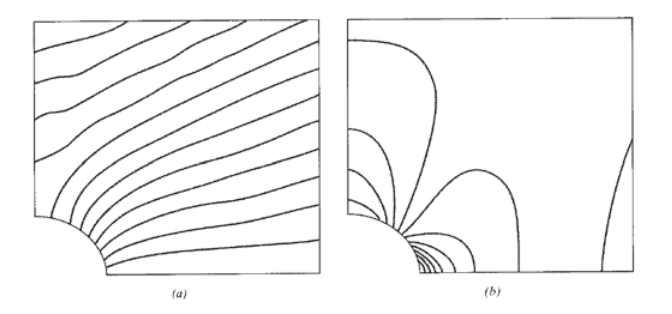
Ejercicio\(\PageIndex{1}\)
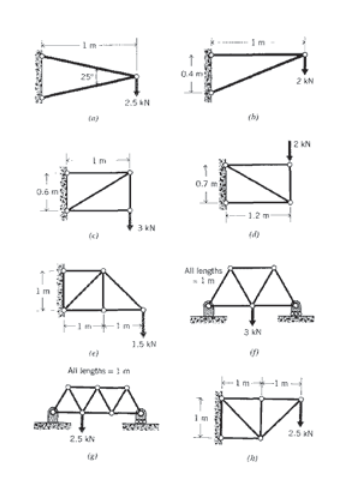
(a) — (h) Utilizar FEA para determinar la fuerza en cada elemento de las cerchas trazadas a continuación.
Ejercicio\(\PageIndex{2}\)
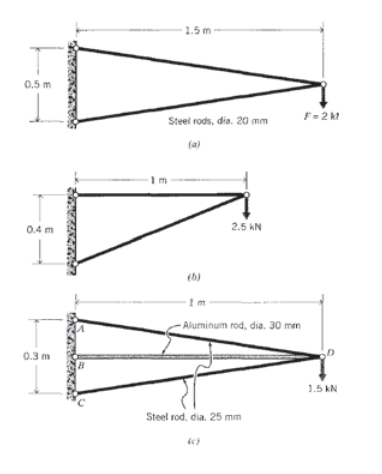
(a) — (c) Redactar las matrices globales de rigidez para las armaduras enumeradas a continuación, y resolver para las fuerzas y desplazamientos desconocidos. Para cada elemento supongamos\(E = 30\) Mpsi y\(A = 0.1 in^2\).
Ejercicio\(\PageIndex{3}\)
Obtenga una solución de elementos finitos de tensión plana para una viga en voladizo con una sola carga en el extremo libre. Utilizar dimensiones elegidas arbitrariamente (pero razonables) y propiedades del material. Trazar las tensiones\(\sigma_x\) y\(\tau_{xy}\) como funciones de\(y\) en una estación arbitraria a lo largo del tramo; también graficar las tensiones dadas por la teoría elemental de flexión de la viga (c.f. Módulo 13) y evaluar la magnitud del error numérico.
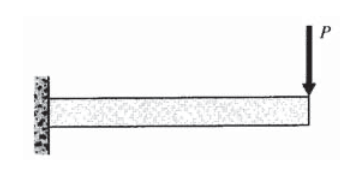
Ejercicio\(\PageIndex{4}\)
Repita el problema anterior, pero con una viga cargada simétricamente en flexión de tres puntos.
Ejercicio\(\PageIndex{5}\)
Utilice elementos axisimétricos para obtener una solución de elementos finitos para la tensión radial en un recipiente a presión de paredes gruesas (usando geometría arbitraria y parámetros de material). Comparar los resultados con la solución teórica (c.f. Prob. 2 en el Módulo 16).


