7: Coeficientes de actividad líquida

Ciencia de la destilación (una mezcla de Química e Ingeniería Química)

Se trata de la Parte VII, Coeficientes de Actividad Líquida de una serie de diez partes de artículos técnicos sobre la Ciencia de la Destilación, como se practica actualmente a nivel industrial. Véase también la Parte I, Panorama general para los comentarios introductorios, los alcances de la serie de artículos y la nomenclatura.

La Parte VII, Coeficientes de Actividad Líquida se basa en la Parte VI, Fugacidad respecto a la salida de los equilibrios vapor-líquido (VLE) de mezclas binarias del comportamiento ideal, como se encuentra comúnmente en la aplicación práctica de la ciencia de la destilación. En conjunto con artículos anteriores, el objetivo de este artículo es completar la explicación del comportamiento de equilibrio de los sistemas binarios; de tal manera que la Parte IX pueda ilustrar un ejemplo de un diseño de proceso de destilación.

En la Parte VI se introdujo la combinación de la Ley de Raoult y la Ley de Dalton que rigen el comportamiento ideal vapor-líquido de las mezclas de fluidos volátiles, repitiéndose la Ecuación 6-1 por conveniencia.

\( Y_{1}=(X_{1} \times VP_{1})/(X_{1} \times VP_{1} + X_{2} \times VP_{2}) \nonumber\)\( Y_{2}=(X_{2} \times VP_{2})/(X_{1} \times VP_{1} + X_{2} \times VP_{2}) \nonumber\)repetir Ecuación 6-1

También en la Parte VI se discutió la desviación del mundo real del comportamiento ideal en cuanto a los coeficientes de fugacidad, pero se detuvo por debajo de los Coeficientes de Actividad Líquida. La ecuación 6-4 repetida a continuación dio la relación completa entre la presión parcial del i-ésimo componente, PP _i, y la presión de vapor de componente puro VP _i, para las fracciones molares de líquido y vapor X _i e Y _i, respectivamente. La presión total del sistema (suma de las presiones parciales) se denota como\(\pi \nonumber\); (\(\phi_{i}^V\nonumber\)&\(\phi_{i}^L\nonumber\)) son los coeficientes de fugacidad de líquido y vapor. \(\gamma_{i} \nonumber\)es el coeficiente de actividad líquida del i-ésimo componente para ese conjunto específico de componentes.

\(Y_{i} \times \pi =PP_{i} =(\phi_{i}^L/ \phi_{i}^V) \times \gamma_{i} \times VP_{i} \times X_{i} \nonumber\)repetir Ecuación 6-4

Se dio un ejemplo en la Parte VI de una mezcla vaporizadora de TCS-STC, contrastando los equilibrios vapor-líquido (VLE) esperados de Raoult/Dalton; de lo que realmente ocurre en el mundo real como resultado de las desviaciones de idealidad. Resumiendo el artículo anterior, el fluido más volátil ejerce un efecto sobre el fluido menos volátil, para aumentar su presión de vapor aparente; y el fluido menos volátil reduce la presión de vapor del fluido más volátil. El efecto neto es hacer que las separaciones de componentes sean más difíciles a través de la destilación (por ejemplo, más bandejas teóricas o mayor cantidad de reflujo de lo esperado). Para una discusión detallada de los coeficientes de fugacidad, véase la Parte VI.

Como nota de “mantenimiento”, debe enfatizarse que las Partes VI y VII tratan los coeficientes de fugacidad y los Coeficientes de Actividad Líquida por separado. En algunos textos, los dos temas se comprimen juntos utilizando modelos específicos de mezcla y Ecuaciones de Estado (EOS). Sin embargo, los dos factores de desviación de idealidad se basan de manera diferente, y su combinación a menudo da resultados erróneos o sin sentido cuando se usan con fluidos polares, o aquellos que tienen un alto grado de enlaces de hidrógeno (como los clorosilanos que se utilizan como ejemplos continuos). Los coeficientes de fugacidad resultan naturalmente de las diferencias en la volatilidad de los fluidos. Los coeficientes de actividad líquida son el resultado de diferencias en las propiedades del fluido, incluyendo temperatura crítica (T _c), presión crítica (P _{c), volumen crítico (V c}) y factor acéntrico (ω), así como los efectos de entropía y entalpía de la mezcla (referidos en textos termodinámicos como exceso de Energía Libre de Gibbs).

Para una temperatura dada y combinación de fluidos, el valor de\(\gamma \nonumber\) es una función de la fracción molar líquida, elevándose asintóticamente desde la unidad en la condición de componente puro. Normalmente, los valores de\(\gamma \nonumber\) para un sistema se representan en función de la fracción molar del componente más volátil. Un ejemplo de dicha gráfica se da en la Figura 7-1, para el binario TCS-STC a 73.9°C (la temperatura del ejemplo continuo de artículos anteriores).

Figura 7-1, Coeficientes de actividad líquida TCS-STC @ 73.9°C

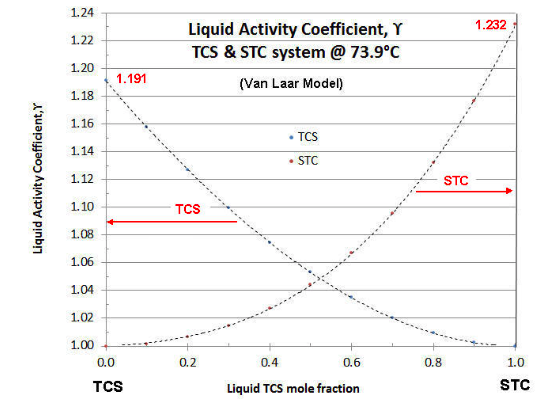
Existen varios modelos para Coeficientes de Actividad Líquida que son termodinámicamente consistentes (es decir, seguir la Regla Gibbs-Duhem de la termodinámica del sistema binario). El modelo de Van Laar de dos constantes es el más fácil de manipular, pero se limita a sistemas binarios. El modelo Margules no es tan diferente del modelo de Van Laar, y también se limita a sistemas binarios. El modelo Wilson es matemáticamente más complejo, pero se puede aplicar a sistemas de componentes ternarios o de mayor numeración. Afortunadamente los parámetros del modelo Wilson se pueden calcular a partir del modelo Van Laar. Se conocen modelos de Coeficientes de Actividad Líquida aún más complejos (por ejemplo, NRTL y UNIQUAC), pero estos requieren más puntos de datos para evaluar de manera efectiva En el caso de la parcela anterior, se muestra el modelo Van Laar. En la Parte VIII se discuten las técnicas para evaluar datos experimentales sobre Coeficientes de Actividad Líquida y ajustar los datos a un modelo. En la mayoría de los casos con clorosilanos (y sus impurezas) la calidad de los datos no es tan grande, por lo que el Van Laar más simple se usa típicamente para correlacionar datos y para evaluar sistemas binarios, y el modelo Wilson se usa para sistemas ternarios y más allá. Para una discusión más profunda de los Coeficientes de Actividad Líquida, se remite al lector al texto "Las propiedades de los gases y líquidos”, de Reid, Prausnitz y Sherwood, (McGraw-Hill). La tercera edición es más legible, pero la quinta edición está más actualizada.

El modelo Van Laar es:

\[Ln(\gamma_{1}) =A_{1} \times [1+(A_{1} \times X_{1})/(A_{2} \times X_{2})]^{-2} \label{7-1} \]

\(Ln(\gamma_{2}) =A_{2} \times [1+(A_{2} \times X_{2})/(A_{1} \times X_{1})]^{-2} \nonumber\)

siendo _A1 y _A2 las constantes Van Laar para el componente más volátil y menos volátil, respectivamente.

Convenientemente,\[EXP(A_{1}) = \gamma_{1} @ X_{2} \rightarrow 0 \label{7-2} \]

\(EXP(A_{2}) = \gamma_{2} @ X_{1} \rightarrow 0 \nonumber\)

lo que simplifica la evaluación. Obsérvese de la Figura 7-1 que la gráfica Coeficientes de Actividad Líquida no siempre es simétrica (es decir, A ₁ ≠ _A2). En la gráfica de la Figura 7-1, A ₁ (TCS) = 0.1752, por lo que la curva TCS asíntotas a\(\gamma \nonumber\) = 1.191; y A ₂ (STC) = 0.2086, por lo que la curva TCS asíntotas a\(\gamma \nonumber\) = 1.232.

Completando el ejemplo en curso de la Parte VI, para una mezcla líquida TCS-STC, con TCS molar al 40%, a 73,9°C, para determinar la fracción molar de vapor en equilibrio (pero ahora incluyendo los efectos del Coeficiente de Actividad Líquida):

En la Parte VI, las presiones de vapor de componentes puros de TCS y STC respectivamente se calcularon a partir de la ecuación VP de la Parte IV para ser de 3.500 y 1.651 atmósferas, respectivamente a 73.9°C. También a partir de la Parte V, las fugacidades de líquido y vapor se calcularon según Cuadro 6-1, repetido a continuación, utilizando la EOS Peng-Robinson (Parte V).

Repetir Tabla 6-1: Comparación de Coeficientes de Fugacidad TCS y STC

	TCS	STC
\(\phi^L \nonumber\)	0.9976	1.0039
\(\phi^V \nonumber\)	1.0488	0.9562
\(\phi^L / \phi^V \nonumber\)	0.9512	1.0498

_{Los valores para\(\gamma \nonumber\) se calculan para TCS y STC @ 0.40 mf TCS, por E quation (\ ref {7-1}) utilizando los valores para A1 y A2 anteriores (o simplemente leídos de la Figura 7-1), para ser 1.075 y 1.027 respectivamente.} Al conectar todos estos valores en la Ecuación 6-4 (repetida anteriormente), las presiones parciales de TCS y STC a 73,9°C son:

\(PP_{TCS} =0.9512 \times 1.075 \times 3.500 \times 0.40 =1.432 \nonumber\)atmósferas, y

\(PP_{STC} =1.0498 \times 1.027 \times 1.651 \times 0.60 =1.068 \nonumber\)atmósferas.

Entonces el valor de\(Y_{TCS} = 1.432/(1.432+1.068) =.573 \nonumber\), que se dio en la Parte VI, siendo la fracción molar STC 0.427.

El lector cuidadoso verá que no sólo las presiones parciales de TCS y STC son diferentes de Raoult/Dalton, sino que también lo es la presión total. En el comportamiento ideal de Raoult/Dalton, las presiones parciales se dieron en la Parte VI como 1.400 y 0.991 atmósferas, para una presión total de 2.39 atmósferas. Pero en realidad, a 73.9°C y 0.40 mf TCS, la presión total sería en cambio de 2.50 atmósferas. Entonces, mientras que las desviaciones de idealidad de TCS hicieron que la fracción molar de vapor fuera más pequeña (0.573 vs 0.586), tanto el TCS como el STC ejercieron una presión ligeramente más parcial de lo que indicaría Raoult. Pero la fracción molar de TCS aún bajó, porque la salida de idealidad de STC fue mayor que la de TCS.

La conclusión de este ejemplo es que si bien Raoult/Dalton le dará un valor “rápido y sucio” para Y/X, es fácil obtener la respuesta incorrecta general para determinar los requisitos de un diseño de columna de destilación. En casi todos los casos de la práctica industrial, el uso de Raoult/Dalton reducirá el número de charolas necesarias para hacer una separación (o para el mismo número de charolas, reducir el tamaño del reflujo requerido). Por ello, es importante saber cómo elaborar la mejor respuesta.

Para muchos sistemas binarios, existen datos VLE, pero normalmente no a la temperatura/presión necesaria para el diseño industrial. La mayoría de los diseños industriales utilizan presiones más altas para economía de tamaño, así como para acomodar las fuentes de energía disponibles para impulsar el rehervidor de columna y el condensador. Sin embargo, los aspectos prácticos de la recolección de datos en el laboratorio generalmente requieren presiones ligeramente por encima de la temperatura ambiente, o en pequeños vacíos. Esto es especialmente cierto en el caso de los clorosilanos, ya que los materiales normales de construcción para presiones más altas pueden catalizar reacciones secundarias lentas, como la desproporción y la dimerización.

Los datos de laboratorio normalmente se recopilan en base a pequeñas cantidades de fluido que se usan repetidamente a combinaciones algo diferentes de temperatura y composición. En el caso de las impurezas electrónicas, algunos de estos compuestos no son muy estables fuera de una matriz de clorosilano. Por lo que se debe utilizar un método de correlación que permita cierto grado de extrapolación.

En 1981 Chung-Ton Lin y Thomas Daubert de la Universidad Estatal de Penn desarrollaron dicho modelo de Coeficiente de Actividad Líquida y publicaron el mismo en Industrial & Engineering Chemistry Process Design and Development, basando su trabajo en mezclas de hidrocarburos no polares. He utilizado su método general, pero modificé dos de las constantes para ajustarse mejor a los datos de VLE disponibles sobre clorosilanos. Usando estas constantes reevaluadas, se utilizó el método revisado “Lin & Daubert” (detallado a continuación como E quation (\ ref {7-3}) para verificar con datos obtenidos industrialmente sobre la purificación por destilación de TCS y silano, con buenos resultados. Obviamente serían preferibles más datos, especialmente sobre mezclas ternarias e impurezas electrónicas de baja concentración en clorosilanos. Sin embargo, hasta que tal esté disponible, se recomienda E quation (\ ref {7-3}) a continuación.

Para desarrollar una expresión genérica para los parámetros de Van Laar (\(A_{i} \nonumber\)&\(A_{j} \nonumber\)), Lin & Daubert remontan a la expresión original de dos términos de Van Laar con respecto al exceso de energía de Gibbs de mezcla, utilizando la Ecuación de Estado SRK para compresibilidad molar parcial y reglas de mezcla simples; y expandirla en lo siguiente:

\[A_{i} = c \times F_{i} +d \times k_{ij} \times G_{i} \label{7-3} \]

\(A_{j} = c \times F_{j} +d \times k_{ij} \times G_{j} \nonumber\)

• \(F_{i} =1/[T_{ri}P_{ci}] \times (R_{i} \times (1+M_{j})^{0.5} \times P_{ci}^{0.5} - R_{j} \times (1+M_{j})^{0.5} \times P_{cj}^{0.5})^2 \nonumber\)
• \(F_{j} =1/[T_{rj}P_{cj}] \times (R_{j} \times (1+M_{i})^{0.5} \times P_{cj}^{0.5} - R_{i} \times (1+M_{i})^{0.5} \times P_{ci}^{0.5})^2 \nonumber\)
• \(G_{i} = T_{ri}^{-1} (P_{cj}/P_{ci})^{0.5} \times R_{i} \times (1+M_{i})^{0.5} \times R_{j} (1+M_{i})^{0.5} \nonumber\)
• \(G_{j} = T_{rj}^{-1} (P_{ci}/P_{cj})^{0.5} \times R_{j} \times (1+M_{j})^{0.5} \times R_{i} (1+M_{j})^{0.5} \nonumber\)
• \(M_{i} = 0.480 + 1.574\omega_{i} -.176\omega_{i}^2 \nonumber\)\(M_{j} = 0.480 + 1.574\omega_{j} -.176\omega_{j}^2 \nonumber\)
• \(R_{i} =[1+M_{i} \times (1-T_{ri}^{0/5})]^{0.5} \nonumber\)\(R_{j} =[1+M_{j} \times (1-T_{rj}^{0/5})]^{0.5} \nonumber\)
• \(k_{ij} =1 - 2 \times [V_{ci}^{1/3} \times V_{cj}^{1/3}]^{0.5} / [V_{ci}^{1/3} + V_{cj}^{1/3}] \nonumber \)

Usando un conjunto mejorado de ajustes de curva para “c”,

• \(0< \Delta \omega <0.03 ⇒ \nonumber\)\( Ln(c)= -8.0637E+04(\Delta \omega)^3 +8.2649E+03(\Delta \omega)^ 2 - 3.2891E+02 (\Delta \omega) +5.5051 \nonumber\)
• \(0.03 < \Delta \omega <0.30 ⇒ \nonumber\)\( Ln(c)=6.4645E+02(\Delta \omega)^4 -7.9857E+02(\Delta \omega)^3 +3.4768E+02(\Delta \omega)^2 -6.5099E+01(\Delta \omega) +2.5667 \nonumber\)

Al reducir los datos de VLE disponibles a los parámetros de Van Laar y ajustar los coeficientes de fugacidad de vapor y líquido, se encontró que el mejor valor de “d” es 112.1 para clorosilanos y fluidos similares.

Lin & Daubert sugirieron que la función “c” se limitara a\(0.005 < \Delta \omega=|\omega_{i} - \omega_{j}| <0.15 \nonumber\), en base a sus datos; pero usar el conjunto mejorado de polinomios anterior para “c” evita singularidades durante los cálculos iterativos, con una “c” mínima de 0.135 (como “Δω” → ∞)

Nótese que la variable “c” en el primer término de la Ecuación 7-3 se basa en los\(F_{i} \nonumber\) valores y las diferencias entre el factor acéntrico de los dos fluidos, ω (es decir, su complejidad molecular); mientras que el segundo término de la Ecuación 7-3 se basa en los\(G_{i} \nonumber\) valores y las diferencias entre los dos fluidos. volúmenes moleculares en crítico (V _c).

---

Volviendo al ejemplo anterior continuo de TCS-STC, y utilizando la temperatura crítica de los dos componentes (T _c), la presión crítica (P _c), el volumen crítico (V _c) y el factor acéntrico (ω), así como basando la temperatura reducida (T _r) en 73.9°C = 347.05°K, E quation (\ ref {7-3}) da los valores de _A1 y _A2 utilizados anteriormente en este artículo, de 0.1752 y 0.2086 respectivamente.

Frecuentemente en la evaluación de diferentes diseños de destilación para un proceso, el diseñador se enfrenta a la necesidad de realizar cambios de temperatura del proceso y determinar el efecto sobre Y/X usando la Ecuación 6-4, repetida anteriormente. Eso no causa ningún problema en la evaluación de la relación de fugacidad\(\phi_{i}^L / \phi_{i}^V \nonumber\), ya que esos factores se derivan de la EOS (ver Parte VI). Sin embargo, si se utilizan valores obtenidos experimentalmente para\(\gamma \nonumber\) que se obtuvieron a una temperatura diferente, se necesita un ajuste adicional. La “regla general” que se ve en algunos textos es que Ln (\(\gamma \nonumber\)) es proporcional a 1/T (temperatura absoluta) para pequeños cambios de temperatura. En realidad, tal “regla general” equivale a hacer una suposición de que los efectos de mezcla del fluido multicomponente están más cerca de un modelo isotérmico que uno isentálpico. En la mayoría de los casos, la dependencia de la temperatura en el coeficiente de actividad es una mezcla de dos modelos teóricos, lo que lleva a la relación:

\[Ln(\gamma_{i})=a + \frac{b}{T} \label{7-4} \]

donde “a” y “b” son las constantes de una relación lineal (“a” = 0 que conduce al modelo isentálpico, o “b” = 0 que conduce al modelo isotérmico). El uso de E quation (\ ref {7-3}) resuelve el problema, ya que predice tales cambios de temperatura a lo largo de las líneas de E quation (\ ref {7-4}), y así se puede utilizar de manera relativa. Por ejemplo, si se encuentra que la cuación E (\ ref {7-3}) sobrepredice el valor de un\(Ln(\gamma) \nonumber\) 10% de un valor de coeficiente de actividad obtenido experimentalmente, entonces calcule cuánta cuación E (\ ref {7-3}) predecirían para las diferentes temperaturas, y aplicaría ese 10% sobre el\(Ln(\gamma) \nonumber\).

Tenga en cuenta que a todos los efectos, el Coeficiente de Actividad del Líquido no es una función directa de la presión, aparte de aumentar la temperatura de ebullición aumenta la presión. No obstante, las fugacidades son una función tanto de la temperatura como de la presión, y es por ello que deberían incluirse en los cálculos Y/X (muchos textos abogan por fijar las fugacidades a la unidad, que sólo está cerca de ser válidas a presiones muy bajas).

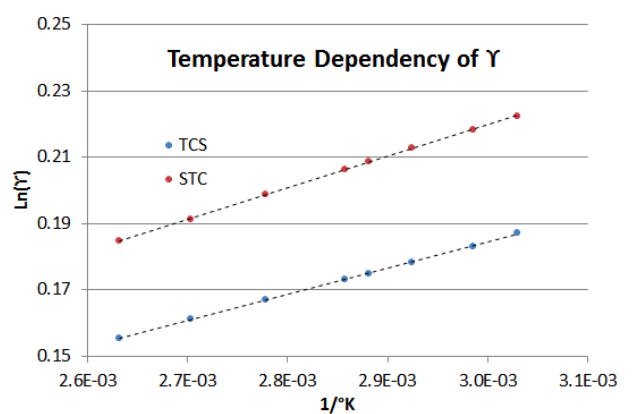
Para demostrar cómo funciona la E quation (\ ref {7-3}) con el cambio de temperatura (de 330°K a 380°K), la Figura 7-2 muestra la dependencia para los BIP asintóticos de la mezcla TCS-STC en el ejemplo anterior. Tenga en cuenta que la pendiente de la línea de Coeficiente de Actividad de Líquido STC es aproximadamente 20% más pronunciada que la de la línea de Coeficiente de Actividad de Líquido TCS (es decir, en el sistema binario TCS-STC, aumentar la temperatura tiene un mayor efecto en los STC\(\gamma \nonumber\) que en los TCS\(\gamma \nonumber\)).

Figura 7-2, Dependencia de temperatura de Ln () en las asíntotas