Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

6.23: Sutiles de Codificación

Última actualización

30 oct 2022
Guardar como PDF
- 6.22: Compresión y el Código Huffman
- 6.24: Codificación de canales

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Algunas sutilezas de la codificación, incluyendo la autosincronización y una comparación de los códigos Huffman y Morse.

En el código Huffman, las secuencias de bits que representan símbolos individuales pueden tener longitudes diferentes, por lo que el índice de flujo de bits m no aumenta en el paso de bloqueo con el índice n de la señal con valor de símbolo. Para capturar la frecuencia con la que se deben transmitir los bits para mantenerse al día con la producción de símbolos de la fuente, solo podemos calcular promedios. Si nuestro código fuente promedia $\overline{B(A)} \nonumber$ bits/símbolo y símbolos se producen a una tasa R, la tasa de bits promedio es igual

$\overline{B(A)}R \nonumber$

y esta cantidad determina la duración T del intervalo de bits.

Ejercicio $\PageIndex{1}$

Calcular la relación entre T y la tasa de bits promedio $\overline{B(A)}R \nonumber$

Solución

$T=\frac{1}{\overline{B(A)}R} \nonumber$

Una sutileza de la codificación fuente es si necesitamos “comas” en el flujo de bits. Cuando usamos un número desigual de bits para representar símbolos, ¿cómo determina el receptor cuándo comienzan y terminan los símbolos? Si creaste un código fuente que requiriera un marcador de separación en el flujo de bits entre símbolos, sería muy ineficiente ya que esencialmente estás requiriendo un símbolo extra en el flujo de transmisión.

Nota

Un buen ejemplo de esta necesidad es el Código Morse: Entre cada letra, el telégrafo necesita insertar una pausa para informar al receptor cuando ocurren los límites de las letras.

Como se muestra en este ejemplo, no se colocan comas en el flujo de bits, pero se puede decodificar sin ambigüedades la secuencia de símbolos del flujo de bits. Huffman demostró que su código (máximamente eficiente) tenía la propiedad de prefijo: Ningún código para un símbolo comenzó el código de otro símbolo. Una vez que se tiene la propiedad prefix, el flujo de bits se autosincroniza parcialmente: Una vez que el receptor sabe dónde comienza el flujo de bits, podemos asignar una secuencia de símbolos única y correcta al flujo de bits.

Ejercicio $\PageIndex{1}$

Esboce un argumento de que la codificación de prefijo, ya sea derivada de un código Huffman o no, proporcionará decodificación única cuando se usa un número desigual de bits/símbolo en el código.

Solución

Debido a que ninguna palabra de código comienza con la palabra de código de otra persona, la primera palabra de código encontrada en un flujo de bits debe ser la correcta. Tenga en cuenta que debemos comenzar por el inicio del flujo de bits; saltar al medio no garantiza una decodificación perfecta. El final de una palabra clave y el comienzo de otra podría ser una palabra clave, y nos perderíamos.

Sin embargo, tener un código de prefijo no garantiza la sincronización total: Después de saltar a la mitad de un flujo de bits, ¿podemos encontrar siempre los límites de símbolo correctos? El problema de la autosincronización mitiga el uso de algoritmos eficientes de codificación de fuentes.

Ejercicio $\PageIndex{1}$

Mostrar con el ejemplo que un flujo de bits producido por un código Huffman no necesariamente se sincroniza automáticamente. ¿Los códigos de longitud fija se sincronizan automáticamente?

Solución

Considera el flujo de bits... 0110111... tomado del flujo de bits 0|10|110|110|111|... Descodificaríamos la parte inicial incorrectamente, luego sincronizaríamos. Si tuviéramos un código de longitud fija (digamos 00,01,10,11), la situación es mucho peor. ¡Saltar al medio lleva a que no haya sincronización en absoluto!

Otro problema son los errores de bit inducidos por el canal digital; si ocurren (y lo harán), la sincronización se puede perder fácilmente incluso si el receptor arrancó “en sincronía” con la fuente. A pesar de las pequeñas probabilidades de error que ofrece el buen diseño del conjunto de señales y el filtro coincidente, un error poco frecuente puede devastar la capacidad de traducir un flujo de bits en una señal simbólica. Necesitamos formas de reducir los errores de recepción sin exigir que p _e sea más pequeño.

Ejemplo $\PageIndex{1}$ :

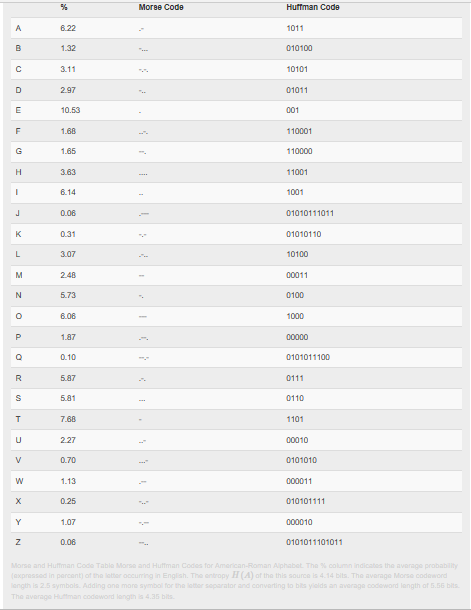
El primer sistema de comunicaciones eléctricas, el telegrama, era digital. Cuando se desplegó por primera vez en 1844, comunicaba texto a través de conexiones por cable usando un código binario, el código Morse, para representar letras individuales. Para enviar un mensaje de un lugar a otro, los operadores de telégrafos tocarían el mensaje usando una clave telegráfica a otro operador, quien transmitiría el mensaje al siguiente operador, presumiblemente acercando el mensaje a su destino. En definitiva, el telégrafo se basó en una red no muy diferente a los conceptos básicos de las redes informáticas modernas. Decir que presagiaba las comunicaciones modernas sería quedarse corto. También estaba muy por delante de algunas tecnologías necesarias, a saber, el Teorema de Codificación de Fuentes. El código Morse, que se muestra en la siguiente tabla, no era un código de prefijo. Para separar los códigos para cada letra, el código Morse requería que se insertara un espacio, una pausa, entre cada letra. En la teoría de la información, ese espacio cuenta como otra letra de código, lo que significa que el código Morse codificaba texto con un código fuente de tres letras: puntos, guiones y espacio. El código fuente resultante no está dentro de un poco de entropía, y es groseramente ineficiente (alrededor del 25%). En la tabla se muestra un código Huffman para texto en inglés, que como sabemos es eficiente.

Objetivos de aprendizaje

Ejercicio6.23.1\PageIndex{1}

Nota

Ejercicio6.23.1\PageIndex{1}

Ejercicio6.23.1\PageIndex{1}

Ejemplo6.23.1\PageIndex{1}:

Support Center

How can we help?

Ejercicio $\PageIndex{1}$

Ejercicio $\PageIndex{1}$

Ejercicio $\PageIndex{1}$

Ejemplo $\PageIndex{1}$ :