Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

3.2: Estructura MOS Básica

Última actualización

30 oct 2022
Guardar como PDF
- 3.1: Introducción a los MOSFET
- 3.3: Voltaje Umbral

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$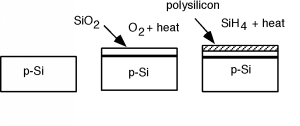

¡CNX se jubila! Los libros de texto de OpenStax siempre estarán disponibles en openstax.org. El contenido creado por la comunidad permanecerá visible hasta agosto de 2022 y luego se trasladará a Internet Archive. Conoce más aquí

Una estructura MOS se forma comenzando con un bloque de silicio tipo p, aplicando gas oxígeno y calor al hecho superior para formar una capa de dióxido de silicio, y aplicando silano y calor a la cara superior de la capa de dióxido de silicio para formar una capa de polisilicio. — Figura $\PageIndex{1}$ : Formación de la estructura MOS

En la figura se $\PageIndex{1}$ muestran los pasos necesarios para realizar la estructura MOS. Nos ayudará en nuestro entendimiento si ahora rotamos nuestra imagen para que esté apuntando de lado en nuestros próximos dibujos. (Además, nos olvidaremos de las dos regiones n por un tiempo, y las recogeremos de nuevo más tarde cuando volvamos a girar la estructura del lado derecho hacia arriba.) La figura $\PageIndex{2}$ muestra la estructura girada. Tenga en cuenta que en el p-silicio tenemos orificios móviles cargados positivamente, y aceptores fijos cargados negativamente. Debido a que lo necesitaremos más adelante, también hemos mostrado el diagrama de bandas para el semiconductor debajo del boceto del dispositivo. Tenga en cuenta que dado que el sustrato es de tipo p, el nivel de Fermi se ubica cerca de la banda de cenefa.

Figura $\PageIndex{2}$ : Estructura MOS básica

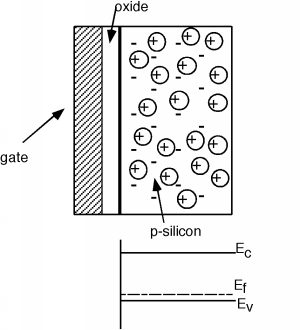
El MOS de la Figura 1 anterior se gira de manera que la puerta de polisilicio está orientada hacia la izquierda y el p-silicio está a la derecha. Se dibuja el diagrama de bandas para el p-silicio, con el nivel Fermi una distancia muy corta por encima de la banda de cenefa. — Figura $\PageIndex{2}$ : Estructura MOS básica

Coloquemos ahora un potencial entre la puerta y el sustrato de silicio. Supongamos que hacemos que la puerta sea negativa con respecto al sustrato. Dado que el sustrato es tipo p, tiene muchos orificios móviles, cargados positivamente en él. Algunos de ellos se sentirán atraídos por la carga negativa en la puerta, y se moverán hacia la superficie del sustrato. Esto también se refleja en el diagrama de bandas debajo del boceto de la estructura en la Figura $\PageIndex{3}$ . Recuerde que la densidad de los agujeros es exponencialmente proporcional a lo cerca que está el nivel de Fermi al borde de la banda de valencia. Vemos que el diagrama de bandas se ha doblado ligeramente cerca de la superficie para reflejar los agujeros adicionales que allí se han acumulado.

Figura $\PageIndex{3}$ : Aplicación de un voltaje de puerta negativo

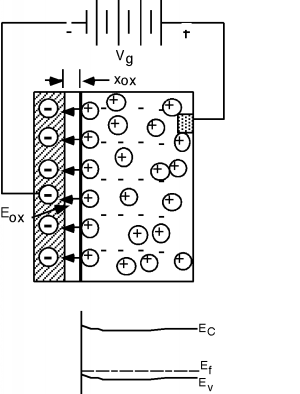
El MOS de la Figura 2 anterior tiene el extremo negativo de una fuente de voltaje conectada a la puerta, y el extremo positivo de la fuente de voltaje conectado al p-silicio. Los electrones se acumulan en la puerta, los agujeros en el p-silicio se mueven hacia el borde izquierdo del p-silicio, y se forma un campo eléctrico e_Ox en la capa de dióxido de silicio de ancho x_ox entre estas dos acumulaciones. En el diagrama de bandas del p-silicio, las bandas de conducción y cenefa ahora se curvan ligeramente hacia arriba en sus extremos más a la izquierda. — Figura $\PageIndex{3}$ : Aplicación de un voltaje de puerta negativo

Se desarrollará un campo eléctrico entre los agujeros positivos y la carga negativa de la puerta. Tenga en cuenta que la puerta y el sustrato forman una especie de condensador de placa paralela, con el óxido actuando como capa aislante entre ellos. El óxido es bastante delgado en comparación con el área del dispositivo, por lo que es bastante apropiado asumir que el campo eléctrico dentro del óxido es uniforme. (Ignoraremos las franjas en los bordes.) La integral del campo eléctrico es solo el voltaje de puerta aplicado $V_{g}$ . Si el óxido tiene un espesor $x_{\text{ox}}$ , entonces dado que $E_{\text{ox}}$ es uniforme, viene dado por $E_{\text{ox}} = \frac{V_{g}}{x_{\text{ox}}}$

Si nos enfocamos en una pequeña parte de la puerta, podemos hacer una pequeña caja de “pastillas” que se extiende desde algún lugar del óxido, a través de la interfaz óxido/puerta y termina dentro del material de la puerta en algún lugar. El pastillero tendrá un área $\Delta (s)$ . Ahora vamos a invocar la ley de Gauss, que revisamos antes. La ley de Gauss simplemente dice que la superficie integral sobre una superficie cerrada del vector de desplazamiento $D$ (que es, por supuesto, solo $\varepsilon$ veces $E$ ) es igual a la carga total encerrada por esa superficie. Supondremos que existe una densidad de carga superficial $-Q_{g}$ , en unidades de $\frac{\mathrm{Coulombs}}{\mathrm{cm}^2}$ sobre la superficie del electrodo de puerta (Figura $\PageIndex{4}$ . La forma integral de la Ley de Gauss es simplemente: $\oint \varepsilon_{\text{ox}} \mathbf{E} \ d \mathbf{S} = Q_{\text{encl}}$

Figura $\PageIndex{4}$ : Encontrar la densidad de carga superficial

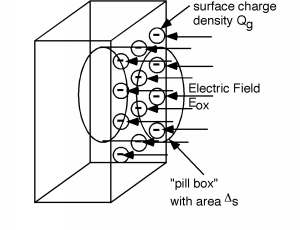
Una pequeña sección en forma de caja de la puerta tiene una densidad de carga superficial Q_g en su lado derecho, un campo eléctrico e_Ox apuntando hacia el lado derecho y un “pastillero” cilíndrico con área transversal Delta s comenzando en la cara derecha de la caja y extendiéndose hacia ella. — Figura $\PageIndex{4}$ : Encontrar la densidad de carga superficial

Tenga en cuenta que hemos utilizado $\varepsilon_{\text{ox}} E$ en lugar de $D$ . En esta configuración particular, la integral es fácil de realizar, ya que el campo eléctrico es uniforme, y solo apunta a través de una superficie, termina en la carga superficial negativa dentro del pastillero. La carga encerrada en el pastillero es justa $Q_{g} \Delta (s)$ , y así tenemos (teniendo en cuenta que la integral superficial de un vector que apunta hacia la superficie es negativa) $\begin{array}{l} \oint \varepsilon_{\text{ox}} \mathbf{E} \ d \mathbf{S} &= -\left( \varepsilon_{\text{ox}} E_{\text{ox}} \Delta (s)\right) \\ &= - \left(Q_{g} \Delta (s)\right) \end{array}$

o $\varepsilon_{\text{ox}} E_{\text{ox}} = Q_{g}$

Ahora, podemos usar Ecuación $\PageIndex{1}$ para obtener $\frac{\varepsilon_{\text{ox}} V_{g}}{x_{\text{ox}}} = Q_{g}$

o $\frac{Q_{g}}{V_{g}} = \frac{\varepsilon_{\text{ox}}}{x_{\text{ox}}} \equiv c_{\text{ox}}$

La cantidad $c_{\text{ox}}$ se llama capacitancia de óxido. Cuenta con unidades de $\frac{\mathrm{Farads}}{\mathrm{cm}^2}$ , por lo que realmente es una capacitancia por unidad de área del óxido. La constante dieléctrica del dióxido de silicio $\varepsilon_{\text{ox}}$ ,, es aproximadamente $3.3 \times 10^{-13} \mathrm{~F} / \mathrm{cm}$ . Un espesor de óxido típico podría ser $250 \AA$ , o $2.5 \times 10^{-6} \mathrm{~cm}$ . En este caso, $c_{\text{ox}}$ sería sobre $1.30 \times 10^{-7} \ \frac{\mathrm{F}}{\mathrm{cm}^2}$ . (Las unidades que estamos usando aquí, si bien pueden parecer un poco arbitrarias y confusas, son las más utilizadas en el negocio de los semiconductores. Te acostumbrarás a ellos en poco tiempo.)

La forma más útil de Ecuación $\PageIndex{6}$ es cuando se da la vuelta: $Q_{g} = c_{\text{ox}} V_{g}$

ya que nos da una manera de encontrar la carga en la puerta en términos del potencial de la puerta. Utilizaremos esta ecuación más adelante en nuestro desarrollo de cómo funciona realmente el transistor MOS.

Resulta que no hemos hecho nada muy útil aplicando un voltaje negativo a la puerta. Allí hemos dibujado más agujeros en lo que se llama una capa de acumulación, pero eso no nos ayuda en nuestro esfuerzo por crear una capa de electrones en el MOSFET que pudiera conectar eléctricamente las dos regiones n juntas.

Demos la vuelta a la batería y apliquemos un voltaje positivo a la compuerta. (En realidad, saquemos la batería del boceto por ahora, y solo dejemos que $V_{g}$ sea un valor positivo, relativo al sustrato que atará a tierra). Hacer $V_{g}$ positivo pone positivo $Q_{g}$ en la puerta. La carga positiva empuja los agujeros lejos de la región debajo de la puerta y descubre algunos de los aceptores fijos cargados negativamente. Ahora el campo eléctrico apunta hacia el otro lado y va desde la carga positiva de la puerta, terminando en la carga aceptora negativa dentro del silicio.

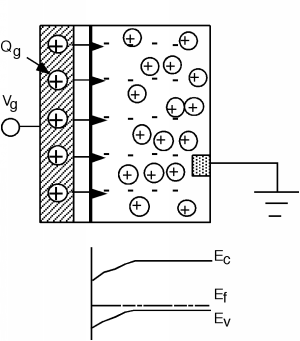
Se aplica un voltaje positivo V_g a la puerta del MOS, generando una acumulación de agujeros con carga Q_g en la puerta. El extremo derecho del p-silicio está unido a tierra, y los agujeros dentro del p-silicio se mueven hacia el lado derecho. Un campo eléctrico se extiende desde las cargas positivas en la puerta hasta las cargas negativas estáticas fijas en el p-silicio. El diagrama de bandas del p-silicio muestra bandas de cenefa y conductancia que comienzan más abajo en el extremo izquierdo y suben gradualmente antes de nivelarse hacia el lado derecho. — Figura $\PageIndex{5}$ : El aumento del voltaje extiende la región de agotamiento más adentro del dispositivo

El campo eléctrico ahora se extiende hacia el semiconductor. Sabemos por nuestra experiencia con la unión p-n que cuando hay un campo eléctrico, hay un cambio en el potencial, que se representa en el diagrama de bandas doblando las bandas. Doblar las bandas hacia abajo (como deberíamos avanzar hacia la carga positiva) hace que la banda de valencia se aleje del nivel de Fermi cerca de la superficie del semiconductor. Si recuerdas la expresión que teníamos para la densidad de agujeros en términos de $E_{v}$ y $E_{f}$ (ecuaciones de densidad de electrones y agujeros) es fácil ver que efectivamente $p = N_{v} e^{- \frac{E_{f} - E_{v}}{kT}}$

hay una región de agotamiento (región casi sin agujeros) cerca de la región debajo de la puerta. (Una vez que $E_{f} - E_{v}$ se hace grande con respecto a $kT$ , el exponente negativo causa $p \rightarrow 0$ .

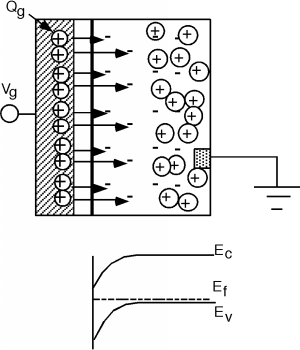
Figura 5 anterior a medida que aumenta la carga positiva acumulada en la puerta. La caída en el extremo izquierdo de las bandas de cenefa y conductancia en el diagrama de bandas es más pronunciada. — Figura $\PageIndex{6}$ : Umbral, $E_{f}$ se está acercando a $E_{c}$

El campo eléctrico se extiende más hacia el semiconductor, ya que se descubre más carga negativa y las bandas se doblan más hacia abajo. Pero ahora tenemos que recordar la ecuación de densidad electrónica, que nos dice cuántos electrones tenemos: $n = N_{c} e^{- \frac{E_{c} - E_{f}}{kT}}$

Un vistazo a la Figura $\PageIndex{6}$ anterior revela que con tanto flexión de banda $E_{c}$ , el borde de la banda de conducción, y $E_{f}$ , el nivel de Fermi, comienzan a acercarse el uno al otro (al menos en comparación con $kT$ ), lo que significa que $n$ , la concentración de electrones, pronto debería comenzar a convertirse significativo. En la situación representada por la Figura $\PageIndex{6}$ , decimos que estamos en umbral, y el voltaje de puerta en este punto se llama el voltaje umbral, $V_{T}$ .

Ahora, aumentemos $V_{g}$ arriba $V_{T}$ . Aquí está el boceto en Figura $\PageIndex{7}$ .

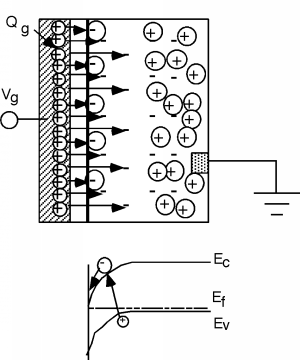
Diagrama de la Figura 6 anterior con un mayor número de agujeros acumulados en la puerta, provocando que una capa de electrones se acumule en el lado del p-silicio más cercano a la puerta. — Figura $\PageIndex{7}$ : Inversión — Los electrones forman una capa de inversión bajo la puerta

A pesar de que hemos aumentado $V_{g}$ más allá del voltaje umbral $V_{T}$ , y aparece más carga positiva en la puerta, la región de agotamiento ya no vuelve a moverse hacia el sustrato. En cambio, los electrones comienzan a aparecer debajo de la región de la puerta, y las líneas de campo eléctrico adicionales terminan en estos nuevos electrones en lugar de en aceptores adicionales. Hemos creado una capa de inversión de electrones bajo la puerta, y es esta capa de electrones la que podemos usar para conectar las dos regiones de tipo n en nuestro dispositivo inicial.

¿De dónde vienen estos electrones? No tenemos donadores en este material, por lo que no pueden venir de ahí. El único lugar desde el que se pudieron encontrar electrones sería a través de la generación térmica. Recuerde, en un semiconductor, siempre hay unos pocos pares de agujeros de electrones que se generan por excitación térmica en un momento dado. Los electrones que se crean en la región de agotamiento son capturados por el campo eléctrico y son barridos hasta el borde por la puerta. He tratado de sugerir esto con el evento de generación de electrones que se muestra en el diagrama de bandas en la figura. En un dispositivo MOS real, tenemos las dos regiones n, y es fácil que los electrones de uno o ambos “caigan” en el pozo potencial bajo la puerta, y creen la capa de inversión de electrones.

Support Center

How can we help?