3.4: Transistor MOS
- Page ID
- 86320
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
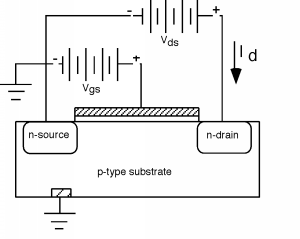
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ahora podemos volver ahora a nuestra estructura inicial, mostrada en la introducción a los MOSFET, solo que esta vez agregaremos una capa de óxido, una estructura de puerta, y otra batería para que podamos invertir la región debajo de la puerta y conectar las dos regiones n juntas. También identificaremos algunos nombres para partes de la estructura, así sabremos de qué estamos hablando. Por razones que quedarán claras más adelante, llamamos a la región n conectada al lado negativo de la batería la fuente, y a la otra la drenadora. Tomaremos tierra la fuente, y también el sustrato tipo p. Agregamos dos baterías:\(V_{\text{gs}}\) entre la puerta y la fuente, y\(V_{\text{ds}}\) entre el desagüe y la fuente.

Será útil si también hacemos otro boceto que nos brinde una vista en perspectiva del dispositivo. Para ello despojamos la puerta y el óxido, pero imaginaremos que hemos aplicado un voltaje mayor que\(V_{T}\) a la puerta, por lo que hay una región tipo n llamada canal que conecta los dos. Supondremos que la región del canal tiene longitud\(L\) y anchura\(W\), como se muestra en la Figura\(\PageIndex{2}\).

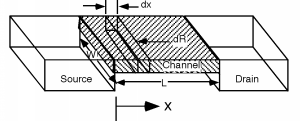
A continuación queremos echar un vistazo a una pequeña sección de canal, y encontrar su resistencia\(dR\), cuando la pequeña sección es\(dx\) larga. \[dR = \frac{dx}{\sigma_{s} W}\]
Hemos introducido una forma ligeramente diferente para nuestra fórmula de resistencia aquí. Normalmente, tendríamos un simple\(\sigma\) en el denominador, y un área\(A\) para el área transversal del canal. Resulta muy difícil averiguar cuál es esa área de sección transversal del canal, sin embargo. Los electrones que forman la capa de inversión se agrupan en una lámina muy delgada de carga superficial que realmente tiene poco o ningún grosor, o penetración en el sustrato.
Si, por otro lado consideramos una conductividad superficial (unidades de\(\mathrm{mhos} = \mho = \Omega^{-1}\)),\(\sigma_{s}\), donde\[\sigma_{s} = \mu_{s} Q_{\text{chan}}\]
entonces tendremos una expresión que podamos evaluar. Aquí,\(mu_{s}\) es una movilidad superficial, con unidades de\(\frac{\mathrm{cm}^2}{\mathrm{V} \cdot \mathrm{sec}}\). Nos encontramos\(\mu\) en capítulos anteriores, cuando estábamos construyendo nuestro modelo de conducción simple. Fue la cantidad la que representó la proporcionalidad entre la velocidad media del portador y el campo eléctrico. \[\bar{v} = \mu E\]\[\mu = \frac{q \tau}{m}\]
La movilidad de la superficie es una cantidad que tiene que medirse para un sistema dado, y generalmente es solo un número que se le da a usted. Algo alrededor\(300 \ \frac{\mathrm{cm}^2}{\mathrm{V} \cdot \mathrm{sec}}\) se trata de lo correcto para el silicio. \(Q_{\text{chan}}\)se llama densidad de carga superficial o densidad de carga de canal y tiene unidades de\(\frac{\mathrm{Coulombs}}{\mathrm{cm}^2}\). Esto es como una hoja de carga, que es diferente de la densidad de carga aparente, que tiene unidades de\(\frac{\mathrm{Coulombs}}{\mathrm{cm}^2}\). Tenga en cuenta que:\[\begin{array}{l} \frac{\mathrm{cm}^2}{\mathrm{Volt} \cdot \mathrm{sec}} \frac{\mathrm{Coulombs}}{\mathrm{cm}^2} &= \frac{\frac{\mathrm{Coul}}{\mathrm{sec}}}{\mathrm{Volt}} \\ &= \frac{I}{V} \\ &= \mho \end{array}\]
Resulta que es bastante sencillo obtener una expresión para\(Q_{\text{chan}}\), la densidad de carga superficial en el canal. Para cualquier voltaje de puerta dado\(V_{\text{gs}}\), sabemos que la densidad de carga en la puerta se da simplemente como:\[Q_{g} = c_{\text{ox}} V_{\text{gs}}\]
Sin embargo, hasta que el\(V_{\text{gs}}\) voltaje de la puerta sea mayor de lo que no\(V_{T}\) estamos creando electrones móviles debajo de la puerta, solo estamos construyendo una región de agotamiento. Definiremos\(Q_{T}\) como la carga en la puerta necesaria para llegar al umbral. \(Q_{T} = c_{\text{ox}} V_{T}\). Cualquier cargo agregado a la puerta anterior\(Q_{T}\) se corresponde con la carga\(Q_{\text{chan}}\) en el canal. Así, es fácil decir:\[Q_{\text{chan}} = Q_{g} - Q_{T}\]
o \[Q_{\text{chan}} = c_{\text{ox}} \left(V_{g} - V_{T}\right)\]
Así, poniendo Ecuación\(\PageIndex{8}\) y Ecuación\(\PageIndex{2}\) en Ecuación\(\PageIndex{1}\), obtenemos:\[d(R) = \frac{d(x)}{\mu_{s} c_{\text{ox}} \left(V_{\text{gs}} - V_{T}\right) W}\]
Si miras hacia atrás en Figura\(\PageIndex{1}\), verá que hemos definido una corriente que\(I_{d}\) fluye hacia el desagüe. Esa corriente fluye a través del canal, y por lo tanto a través de nuestra poca resistencia incremental\(dR\), creando una caída de voltaje\(d \left(V_{c}\right)\) a través de él, donde\(V_{c}\) está el voltaje del canal. \[\begin{array}{l} d \left(V_{c} (x)\right) &= I_{d} d(R) \\ &= \frac{I_{d} d(x)}{\mu_{s} c_{\text{ox}} \left(V_{\text{gs}} - V_{T}\right) W} \end{array}\]
Movamos el denominador a la izquierda, e integremos. Queremos hacer nuestra integral completamente a lo largo del canal. El voltaje en el canal\(V_{c} (x)\) va\(0\) de la izquierda a\(V_{\text{ds}}\) la derecha. Al mismo tiempo,\(x\) va de\(0\) a\(L\). Así nuestros límites de integración serán\(0\) y\(V_{\text{ds}}\) para la integral de voltaje de\(d \left(V_{c} (x)\right)\) y de\(0\) a\(L\) para la integral de\(dx\). \[\int\limits_{0}^{V_{\text{ds}}} \mu_{s} c_{\text{ox}} \left(V_{\text{gs}} - V_{T}\right) W \ d V_{c} = \int\limits_{0}^{L} I_{d} \ dx\]
Ambas integrales son bastante triviales. Intercambiemos el orden de la ecuación, ya que normalmente queremos\(I_{d}\) en función de los voltajes aplicados. \[I_{d} L = \mu_{s} c_{\text{ox}} W \left(V_{\text{gs}} - V_{T}\right) V_{\text{ds}}\]
Ahora simplemente dividimos ambos lados por\(L\), y terminamos con una expresión para la corriente de drenaje\(I_{d}\) en términos de la tensión drenaje-fuente\(V_{\text{ds}}\), la tensión\(V_{\text{gs}}\) de puerta y algunos atributos físicos del transistor MOS. \[I_{d} = \left(\frac{\mu_{s} c_{\text{ox}} W}{L} \left(V_{gs} - V_{T}\right) \right) V_{ds}\]


