3.8: Inversores y Lógica

Como ya sabe, o lo descubrirá en breve, al tomar una clase en lógica digital, los circuitos lógicos se basan principalmente en un circuito llamado inversor. Un inversor simplemente toma una señal y te da la opuesta. Por ejemplo, si se coloca un alto voltaje (un “uno”) en la entrada de un inversor, devuelve un voltaje bajo (un “cero”). La figura\(\PageIndex{1}\) es un inversor simple basado en un transistor MOSFET:

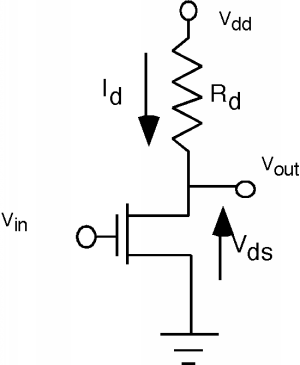Figura\(\PageIndex{1}\): Circuito inversor

Si\(V_{\text{in}}\) es cero, el MOSFET se apaga (\(V_{\text{gs}} < V_{T}\)) y por lo tanto no fluye corriente a través de la resistencia, y\(V_{\text{out}} = V_{\text{dd}}\), un alto. Si\(V_{\text{in}}\) es alto (y suponemos que\(V_{T}\) para el MOSFET es significativamente menor que\(V_{\text{in}}\)) entonces el transistor se enciende, y si\(R\) y\(\frac{W}{L}\) se eligen de manera que la corriente suficiente fluya\(R\) a través para caer la mayor parte de\(V_{\text{dd}}\) él, entonces\(V_{\text{out}}\) será baja.

La forma en que esto se suele describir es a través de una función de transferencia que nos dice cuál es la tensión de salida en función de la tensión de entrada. Hagamos una digresión por solo un minuto y veamos cómo se puede llegar a tal función. Mirando hacia atrás en Figura\(\PageIndex{2}\) debería ser fácil ver que\[V_{\text{dd}} = I_{d} R_{d} + V_{\text{ds}}\]

Podemos reescribir esto como una ecuación para\(I_{d}\). \[I_{d} = \frac{V_{\text{dd}}}{R_{d}} - \frac{V_{\text{ds}}}{R_{d}}\]

Esto se llama ecuación de línea de carga. Dice que\(I_{d}\) varía linealmente con\(V_{\text{ds}}\) (con una pendiente negativa) y tiene un desplazamiento vertical de\(\frac{V_{\text{dd}}}{R_{d}}\). Supongamos que tenemos el transistor MOSFET para el que ya hemos trazado las curvas características en una gráfica anterior. Vamos a dejar\(V_{\text{dd}} = 5 \mathrm{~Volts}\), y dejar\(R_{d} = 1 \mathrm{~k} \Omega\). De la Ecuación\(\PageIndex{2}\) podemos ver que cuándo\(V_{\text{ds}} = 0\),\(I_{d}\) será\(5 \mathrm{~mA}\), y cuándo\(V_{\text{ds}} = V_{\text{dd}}\),\(I_{d}\) será\(0\). Esto nos da entonces una línea recta en la gráfica curva característica que se llama la línea de carga. Esto se muestra en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Curvas características con línea de carga

Al mirar hacia atrás en el esquema para el inversor en la Figura\(\PageIndex{1}\), vemos que la misma corriente\(I_{d}\) fluye a través de la resistencia de carga\(R_{d}\) y a través del transistor. Así, el valor correcto de corriente y voltaje para el circuito para cualquier voltaje de puerta dado es la solución simultánea de la ecuación de línea de carga y el comportamiento del transistor, que, por supuesto, es solo la intersección de la línea de carga con la curva característica apropiada. Por lo tanto, es una simple cuestión de trazar líneas verticales hacia abajo desde cada\(V_{\text{in}}\) curva o\(V_{\text{gs}}\) valor hasta el eje horizontal para averiguar cuál será el voltaje apropiado\(V_{\text{dd}}\) o de salida para el inversor. Suponiendo que\(V_{\text{in}}\) sólo sube a 5 voltios, la curva resultante que obtenemos se ve como Figura\(\PageIndex{3}\). Esta no es una gran característica de transferencia. \(V_{\text{in}}\)tiene que hacerse bastante grande antes de que\(V_{\text{out}}\) empiece a caer, e incluso con la entrada completa de 5 voltios,\(V_{\text{out}}\) sigue siendo mayor que 1 voltio. Escoger un transistor con una resistencia de carga pequeña\(V_{T}\) y una mayor nos daría una mejor respuesta, pero al menos con este ejemplo se puede ver lo que está pasando.

Figura\(\PageIndex{3}\): Características de transferencia para el circuito inversor.

Basándonos en este sencillo circuito inversor, podemos construir circuitos que realizan la función NOR y NAND. \[C_{\text{out}} = \neg \ (A+B)\]

y\[C_{\text{out}} = \neg \ (AB)\]

Debería, a estas alturas, ser obvio para usted cómo los dos circuitos de la Figura\(\PageIndex{4}\) pueden realizar la función NAND y NOR. Resulta que con la capacidad de hacer NAND y NOR, podemos construir cualquier tipo de función lógica que deseemos.

Figura\(\PageIndex{4}\): Circuitos NAND y NOR

Veamos el inversor un poco más de cerca. Por lo general, la carga para el inversor será la siguiente etapa de lógica que, junto con el cableado de interconexión asociado, podemos modelar como un simple condensador. El valor de la capacitancia variará, pero será del orden de\(10^{-12} \mathrm{~F}\).

Figura\(\PageIndex{5}\): Conducción de una carga capacitiva

Cuando la entrada al inversor cambia instantáneamente a un valor bajo, la corriente dejará de fluir a través del transistor, y en su lugar comenzará a cargar la capacitancia de carga. El voltaje de salida seguirá la curva de\(\mathrm{RC}\) carga habitual con una constante de tiempo dada solo por el producto de los\(R\) tiempos\(C\). Si\(C\) es\(10^{-13} \mathrm{~F}\) así, entonces para conseguir un tiempo de subida de\(1 \mathrm{~ns}\) tendríamos que hacer\(R\) sobre\(10^{4} \ \Omega\).

Como veremos más adelante, es prácticamente imposible hacer una\(10 \mathrm{~k} \Omega\) resistencia utilizando técnicas de circuito integrado. Recuerda:\[R = \frac{\rho L}{A}\]

Y así, para obtener una resistencia realmente grande necesitamos ya sea una muy pequeña\(A\) (demasiado difícil de lograr y controlar), una realmente grande\(L\) (ocupa demasiado espacio en el chip) o una enorme\(\rho\) (de nuevo, muy difícil de controlar cuando se llega a las densidades de dopaje muy bajas que se requerirían).

Incluso si pudiéramos encontrar la manera de construir resistencias de circuito integrado tan grandes, todavía habría un problema. La corriente que fluye a través de la resistencia cuando el MOSFET está encendido sería aproximadamente\[\begin{array}{l} I &= \frac{V}{R} \\ &= \frac{5 \mathrm{~V}}{10^{4} \ \Omega} \\ &= 5 \times 10^{-4} \mathrm{~A} \end{array}\]

Esto no parece muy actual hasta que se considera que un microprocesador de Pentium© tiene alrededor de 6 millones de puertas en él. ¡Esto significaría una corriente neta de\(-300 \mathrm{~Amps}\) fluir hacia el chip de la CPU! Tenemos que llegar a una mejor solución.