6.1: Introducción a los fasores

Última actualización
Guardar como PDF

Page ID: 86581

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

No siempre estaremos tratando con líneas de transmisión excitadas con un pulso. Aunque este es un buen modelo para circuitos digitales, no siempre se aplicará. Cuando vayamos a señales analógicas (rf, analógicas de alta frecuencia, etc.) necesitaremos más herramientas de las que tenemos a nuestro alcance en este punto. En un pasado no muy lejano, el material que a continuación consideraremos comenzaba a considerarse pasé. El espectro rf estaba más o menos llenado, y la consigna era “digital”. Ahora, en la nueva era de la comunicación inalámbrica, los teléfonos celulares y las redes de área local rf, la demanda de ingenieros que comprendan el comportamiento de la CA en las líneas de transmisión y que puedan diseñar sistemas que funcionen bien con señales de rf son muy demandadas. Preste atención a lo que decimos aquí, y bien podría encontrarse con muchas ofertas de trabajo lucrativas en el futuro.

Para comenzar, queremos considerar una línea de transmisión que está siendo excitada con una fuente oscilante, como en la Figura\(\PageIndex{1}\).

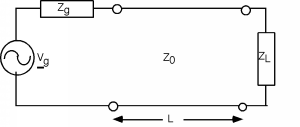Una fuente de voltaje sinusoidal de V_g y una impedancia de fuente Z_g están conectadas al extremo izquierdo de una línea de transmisión de longitud L e impedancia Z_0. El extremo derecho de la línea está unido a una impedancia de carga Z_L.

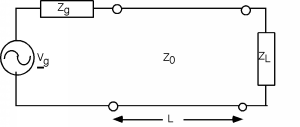
La configuración habitual incluye una fuente, con una salida sinusoidal, una impedancia de fuente\(Z_{g}\), a transmission line with impedance \(Z_{0}\), length \(L\) meters, and a load of impedance \(Z_{L}\) at the end.

Let's look at the source first. We can describe the output waveform from the generator as \[V(t) = V_{g} \cos (\omega t + \theta)\]

When plotted, this looks like Figure \(\PageIndex{2}\).

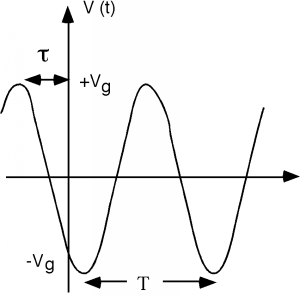Graph of the oscillating output waveform from the voltage source, as a function of time. The cosine waveform has amplitude V_g, period T, and an offset value of tau towards the left.

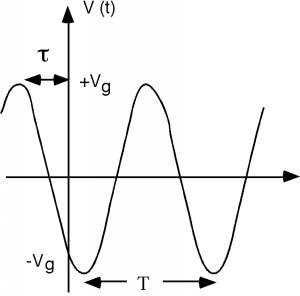
La forma de onda oscilante tiene un período\(T\) y su frecuencia angular\(\omega\) se da como\[\begin{array}{l} \omega &=& \dfrac{2 \pi}{T} \\ &=& 2 \pi f \end{array}\]

El ángulo\(\theta\), que especifica cuánto conduce la onda una función coseno con compensación cero, viene dado por\[\theta = 2 \pi \frac{\tau}{T}\]

Lo que no queremos hacer es llevar un montón de funciones sinusoidales y cosenales alrededor con nosotros por todas partes. Una vez que empezamos a multiplicar y dividirnos, el trigonometría se convierte en un gran lío, y se interpone en nuestra comprensión de lo que está pasando. La forma en que tratamos esto es introducir fasores.

Ya que sabemos de Euler's Identity\[V_{g} e^{i(\omega t + \theta)} = V_{g} (\cos (\omega t + \theta) + i \sin (\omega t + \theta))\]

si tomamos una parte real de\(V_{g} e^{i (\omega t + \theta)}\), extraeremos la forma de onda de voltaje que deseamos. Volveremos a escribir esta función como\[V_{g} e^{i (\omega t + \theta)} = V_{g} e^{i \omega} e^{i \omega t}\]

y luego definir\(\tilde{V}_{g}\) como el voltaje de fasor donde\[\tilde{V}_{g} = V_{g} e^{i \theta}\]

Tenga en cuenta que\(\tilde{V}_{g}\) es una cantidad compleja, con tanto una magnitud\(\left| V_{g} \right|\) como un ángulo de fase\(\theta\). Para recuperar una señal de voltaje real de un fasor, tenemos que multiplicar el fasor por\(e^{i \omega t}\) y luego tomar la parte real. Obsérvese que esto es lo mismo que trazar el fasor en el plano complejo, y luego observar la proyección del fasor sobre el eje real, ya que el fasor gira alrededor a una velocidad\(\omega t\) como se muestra en la Figura\(\PageIndex{3}\).

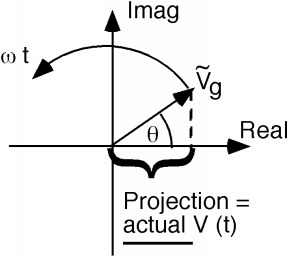Un plano de coordenadas bidimensional tiene un eje horizontal que representa el componente real de un número complejo y un eje vertical que representa el componente imaginario. Un fasor V_g se representa como un vector con su cola en el origen y su cabeza actualmente ubicada en el primer cuadrante, en un ángulo de theta por encima del eje horizontal. La proyección del vector sobre el eje horizontal es el valor real de V (t). El vector gira alrededor del origen en sentido contrario a las agujas del reloj, a la velocidad de theta t.

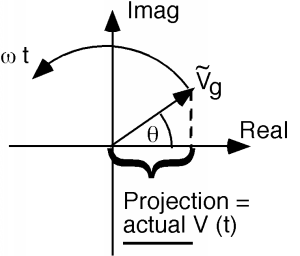
Este método de visualización a veces ayudará a que los resultados parezcan un poco más fáciles de entender, o al menos verificar si son razonables.