1.10: Paquetes de onda e incertidumbre

Ahora tenemos dos formas de describir un electrón. Podríamos describirlo como una onda plana, con número de onda y frecuencia angular definidos con precisión:

\[ \psi(x,t) = e^{i(k_{0}x-\omega_{0}t)} \nonumber \]

Pero como hemos visto, la densidad de intensidad/probabilidad de la onda plana es uniforme en todo el espacio (y en todo el tiempo). Así, la posición del electrón es perfectamente incierta —es que la distribución de probabilidad es uniforme en todas partes de todo el universo. En consecuencia, una onda plana no suele ser una buena descripción para un electrón.

Por otro lado, podríamos describir al electrón como una partícula puntual idealizada

\[ \psi(x,t)=\delta(x-x_{0},t-t_{0}) \nonumber \]

existente en una posición y tiempo definidos con precisión. Pero la densidad de probabilidad de la partícula puntual es uniforme en todo el espacio k y el dominio de frecuencia. Veremos en la siguiente sección que esto significa que la energía y el impulso del electrón son perfectamente inciertos, es decir, las energías electrónicas arbitrariamente grandes y los momentos son posibles.

La única alternativa es aceptar una descripción imprecisa del electrón tanto en el espacio real como en el espacio k, el tiempo y el dominio de la frecuencia. Una oscilación localizada en ambas representaciones se llama paquete de ondas. Una forma común de paquete de ondas es la gaussiana. Por ejemplo, en lugar de la función delta, podríamos describir la posición del electrón como

\[ \psi(x) = a\text{ exp}[-\frac{1}{4}(\frac{x}{\sigma_{x}})^{2}] \nonumber \]

Esta función fue elegida de tal manera que la distribución de probabilidad del electrón es

Figura\(\PageIndex{1}\): Un gaussiano normalizado. El gaussiano tiene la misma forma en el espacio real y en el espacio k. Tenga en cuenta que un gaussiano se aproxima a una función delta en el límite\(\sigma_{x} \rightarrow 0\).

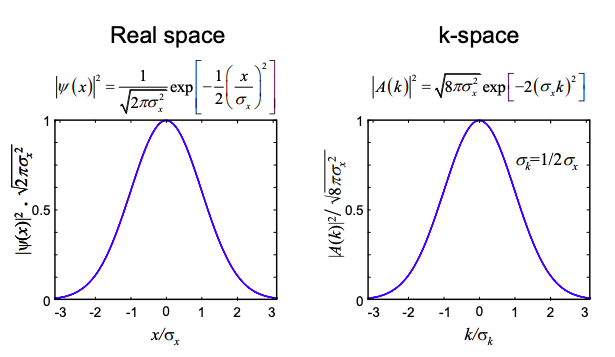
\[ |\psi(x)|^{2} = |a|^{2} \text{ exp}[-\frac{1}{2}(\frac{x}{\sigma_{x}})^{2}] \nonumber \]

donde\(\sigma_{x}\) está la desviación estándar. \(\sigma_{x}\)mide el ancho del gaussiano y a menudo se piensa en ella como la incertidumbre en la posición del electrón. La constante, a, se determina normalizando la densidad de probabilidad sobre todo el espacio, es decir, integrando la Ecuación (1.10.4) sobre x, obtenemos

\[ a=(2\pi \sigma_{x}^{2})^{-1/4} \nonumber \]

Estrictamente, la incertidumbre de una cantidad dada se define por

\[ \sigma^{2} = \langle(x-\langle x\rangle)^{2}\rangle \nonumber \]

\( = \langle x^{2}-2x\langle x\rangle+\langle x\rangle^{2}\rangle \)

donde\(\langle x\rangle\) significa el valor promedio o expectativa de x. Porque\(\langle x\rangle\) es una ecuación constante (1.10.6) puede simplificarse:

\[ \sigma^{2}= \langle x^{2}\rangle-2\langle x \rangle \langle x\rangle+\langle x\rangle^{2} \nonumber \]

\( = \langle x^{2}\rangle-\langle x\rangle^{2} \)

Lo dejaremos como un ejercicio para demostrar que para la densidad de probabilidad gaussiana:

\[ \sigma^{2} = \int x^{2} |\psi(x)|^{2}dx = \sigma_{x}^{2} \nonumber \]

Así, el gaussiano es una opción conveniente para describir un paquete de ondas porque tiene una incertidumbre fácilmente definida.

En el espacio k, el electrón también es descrito por un gaussiano (esta es otra de las propiedades convenientes de esta función). Aplicación de la transformada de Fourier en la Ecuación (1.9.2) y algo de álgebra da

\[ A(k)=(8\pi\sigma_{x}^{2})^{1/4}\text{ exp}[-\sigma_{x}^{2}k^{2}] \nonumber \]

La distribución de probabilidad en el espacio k es

\[ |A(k)|^{2}=(8\pi\sigma_{x}^{2})^{1/2}\text{ exp}[-2\sigma_{x}^{2}k^{2}] \nonumber \]

Así, la incertidumbre en el espacio k es

\[ \frac{1}{2\sigma_{k}^{2}} = 2\sigma_{x}^{2} \nonumber \]

El producto de las incertidumbres en el espacio real y k es

\[ |\sigma_{x}\sigma_{k}| = \frac{1}{2} \nonumber \]

El producto\(|\sigma_{x}||\sigma_{k}| \geq |\sigma_{x}\sigma_{k}|\). Por lo tanto,

\[ |\sigma_{x}||\sigma_{k}| \geq \frac{1}{2} \nonumber \]