1.17: Momentum y Energía
- Page ID
- 84480
Dos experimentos clave revolucionaron la ciencia a principios del siglo XX. Ambos experimentos implican la interacción de la luz y los electrones. Ya hemos visto que los electrones son mejor descritos por las ondas. De igual manera, la luz es transportada por un paquete de ondas llamado fotón. El primer fenómeno, el efecto fotoeléctrico, se explicó asumiendo que la energía de un fotón es proporcional a su frecuencia. El segundo fenómeno, el efecto Compton, se explicó al proponer que los fotones llevan impulso. Que la luz debiera poseer propiedades de partículas como el momento era completamente inesperado antes del advenimiento de la mecánica cuántica.
El efecto fotoeléctrico
No es fácil sacar electrones de un sólido. Están ligados por su atracción hacia núcleos positivos. Pero si damos un electrón en una energía lo suficientemente sólida, podemos superar la energía de unión y liberar un electrón. La energía mínima requerida se conoce como la función de trabajo, W.
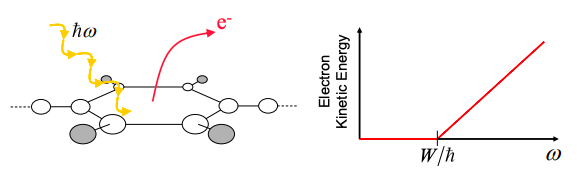
Al bombardear superficies metálicas con luz, se observó que los electrones sólo podían liberarse si la frecuencia de la luz excedía un valor crítico. Por encima de la frecuencia mínima, los electrones se liberaron con mayor energía cinética.
Einstein explicó el efecto fotoeléctrico postulando que, en un fotón, la energía era proporcional a la frecuencia:
\[ E = \hbar\omega \nonumber \]
Dónde\(h = 6.62 \times 10^{-34} Js\) está la constante de Planck, y es la taquigrafía de\(\hbar=h/2\pi\). Tenga en cuenta las unidades para la constante de Planck — energía × tiempo. Esto es útil para recordar al verificar que tus cálculos cuánticos tengan sentido.
Así, la energía cinética de los electrones emitidos viene dada por
\[ \text{electron kinetic energy} = \hbar\omega-W \nonumber \]
Esta técnica todavía se utiliza para sondear la estructura energética de los materiales
Tenga en cuenta que normalmente expresaremos la energía de los electrones en “electrón Voltios (eV)”. La unidad SI para energía, el Joule, suele ser demasiado grande para una discusión conveniente de las energías electrónicas. Una unidad más conveniente es la energía requerida para mover un solo electrón a través de una diferencia de potencial de 1V. Así,\(1\ eV = q\ J\), donde q es la carga sobre un electrón (\(q \sim 1.602\times 10^{-19}\ C\)).
El efecto Compton
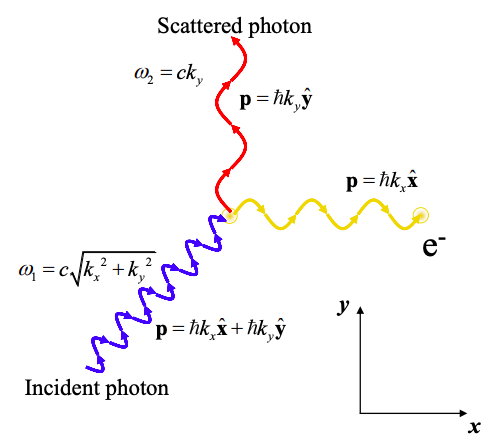
Si un fotón choca con un electrón, se observa que la longitud de onda y la trayectoria del fotón cambian. Después de la colisión el fotón disperso se desplaza al rojo, es decir, su frecuencia se reduce y su longitud de onda se extiende. La trayectoria y la longitud de onda del fotón se pueden calcular asumiendo que el fotón lleva impulso:
\[ p = \hbar k \nonumber \]
donde el número de onda k está relacionado con la frecuencia por
\[ k = \frac{2\pi}{\lambda} = \frac{\omega}{c} \nonumber \]
donde c es la velocidad de la luz.
Estas dos relaciones:\(E=\hbar \omega\) y\(p=\hbar k\) son estrictamente ciertas solo para ondas planas con valores definidos con precisión de ω y k. De lo contrario, debemos emplear operadores para el impulso y la energía. Basándonos en los operadores que definimos anteriormente para k y ω, definimos operadores para momentum
\[ \hat{p} = -i\hbar \frac{d}{dx} \nonumber \]
y energía
\[ \hat{E} = i\hbar \frac{d}{dt} \nonumber \]
Recordemos que cada operador actúa sobre la función a su derecha; y eso no\(\hat{p}\psi\) es necesariamente igual a\(\psi \hat{p}\).