6.2: Energía cuantizada y fotones
- Page ID
- 1935
OBJETIVOS
- Comprender dónde falla la física clásica.
- Aprender qué es la cuantización de la energía.
Hacia fines del siglo XIX, muchos físicos pensaban que su disciplina iba encaminada a explicar todos los fenómenos naturales. Podían calcular el movimiento de objetos a través de las Leyes de Newton, y describir las ondas electromagnéticas a través de las ecuaciones de Maxwell, desarrolladas en 1873 por James Clerk Maxwell, un físico escocés. El universo parecía un lugar simple y ordenado, compuesto de partículas de cierta masa y cuya ubicación y movimiento podía ser finamente descripto; por otro lado, estaba la radiación electromagnética, sin masa y cuya posición exacta no podía ser precisada. Pronto, sin embargo, los científicos observaron ciertos fenómenos que no podían ser explicados por las teorías de su tiempo.
Radiación del cuerpo negro
La radiación del cuerpo negro es la radiación emitida por un cuerpo a cierta temperatura, independientemente de su composición o superficie. La intensidad de emisión a cada longitud de onda es función de la temperatura (Figura \(\PageIndex{2}\)). Y la teoría física clásica no podía explicar su forma.


Figura \(\PageIndex{1}\): Radiación del cuerpo negro. Al calentarse, los objetos emiten radiación electromagnética cuya longitud de onda (y color) depende solo de su temperatura. A temperatura relativamente baja, se ve rojo, al elevarse como en la superficie del sol, se observa blanco o amarillo. Las imágenes son reproducidas con el permiso de Wikipedia.
Existen ejemplos cotidianos de este fenómeno, entre ellos, la resistencia de una cocina o de una estufa eléctrica resplancede rojo o naranja al ser calentada. En cambio, el tungsteno de una lámpara incandescente, mucho más caliente, emite una luz amarillenta. Pero veamos un poco más.
La intensidad de radiación es una medida de la energía emitida por unidad de área. Un gráfico de la intensidad de radiación del cuerpo negro en función de la longitud de onda, para un objeto a varias temperaturas, se muestra en la Figura \(\PageIndex{2}\). Una de las hipótesis más fuertes del físico clásico era que la energía incrementaba o decrecía en forma suave y continua. Por ejemplo, el físico clásico predecía que, al decrecer la longitud de onda, la intensidad radiación que un cuerpo emite debía aumentar a todas las temperaturas, en una curva suave e ilimitadamente. La Figura \(\PageIndex{2}\) expone la predicción teórica para 6000K (línea a trazos). Entonces, la física clásica no explicaba el repentino decrecimiento en la intensidad de radiación emitida a longitudes de onda cortas (comenzando en la región ultravioleta del espectro). Se denominó a esta incongruencia como 'la catástrofe ultravioleta'.
En 1900, sin embargo, el físico alemán Max Planck (1858-1947), explicó la catástrofe ultravioleta proponiendo que la energía de las ondas electromagnéticas está cuantizada, es decir, no es continua. Esto implicaba que, para cada temperatura, hay una intensidad máxima de radiación que es emitida por el cuerpo negro, correspondiente a los picos en la Figura \(\PageIndex{2}\), y así la intensidad no seguía la curva suave y creciente con la temperatura que predecía la física clásica. La energía solo podía ser absorbida o liberada en múltiplos enteros de cierta unidad pequeña de energía, un cuanto.
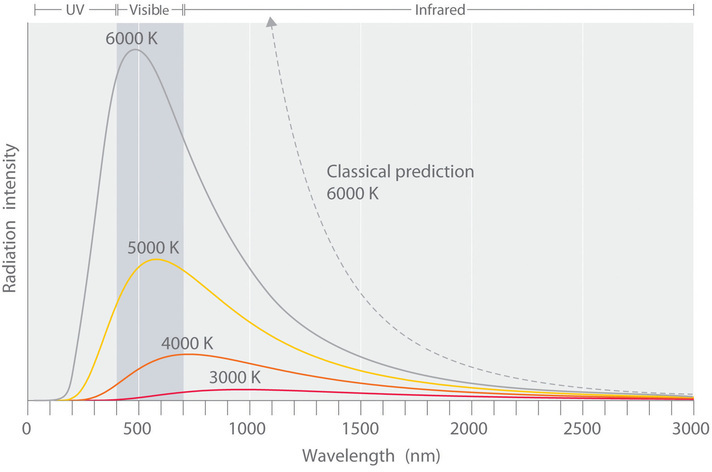
Figura \(\PageIndex{2}\): Temperatura de un objeto vs espectro de emisión (radiación de cuerpo negro). A temperatura baja, emite principalmente longitud de onda mayor a 700 nm (infrarrojo). Al incrementar la temperatura del objeto, el máximo de intensidad se desplaza a longitudes de onda más cortas. Sucesivamente se ve rojo, naranja, amarillo y finalmente blanco. A elevada temperatura todas las longitudes de onda visibles son emitidas en intensidades muy similares. El espectro de luz blanca de un objeto a 6000K se aproxima al espectro de luz solar (Figura \(\PageIndex{1}\)). Bajo 400 nm ocurre la catástrofe ultravioleta, es decir, donde la predicción clásica falla en ajustar la curva experimental.
Max Planck (1858–1947)
Además de físico, Planck era un dotado pianista, y consideraba la música como una carrera. En la década de 1930, Planck sintió su deber permanecer en Alemania, sin importar su abierta oposición al gobierno Nazi.
Uno de sus hijos fue ejecutado en 1944 por participar en un intento, sin éxito, de asesinar a Hitler; y los bombardeos en la última semana de la Segunda Guera Mundial destruyeron la casa de Planck. Luego de la IIGM, se creó la mayor organización de investigación científica, la Sociedad Max Planck, en su honor.
Aunque la cuantización puede parecer un concepto raro, es muy frecuente. Por ejemplo, la moneda es múltiplo entero del centavo (que es la unidad). Similarmente, los intrumentos musicales como el piano o la trompeta solo pueden producir ciertas notas musicales, como C o F. Al no poder producir un rango continuo de frecuencias, sus frecuencias están cuantizadas. Incluso la carga eléctrica está cuantizada: un ión puede tener carga -1 o -2, pero no -1.33.
Planck postuló que la energía de un fotón de cierta radiación estaba dada por la ecuación:
\[ E=h \nu \label{6.2.1}\]
donde la constante de proporcionalidad \(h\) se denomina constante de Planck, y es una de las más precisas. Para nuestros propósitos, su valor con cuatro cifras significativas es suficiente:
\[h = 6.626 \times 10^{−34}\, J•s\, (\text{joule-segundos})\nonumber\]
La ecuación \ref{6.2.1}, muestra que al incrementar la frecuencia de la radiación, la magnitud asociada al cuanto de energía radiante incrementa. Asumiendo que la energía solo puede ser emitida por el objeto en múltiplos enteros de \(hν\), Planck desarrolló una ecuación que concuerda con los resultados experimentales mostrados en la Figura \(\PageIndex{2}\), para la emisión del cuerpo negro. Conceptualmente, puede entenderse la explicación de Planck sobre la catástrofe ultravioleta como sigue: a bajas temperaturas el cuerpo negro solo emite radiación de baja frecuencia, correspondiente a cuantos de baja energía. Al ir incrementando la temperatura del objeto, la probabilidad de emitir un fotón de mayor frecuencia, correspondiente a un cuanto de más energía, incrementa. A toda temperatura es más probable la pérdida de energía por emisión de muchos cuantos poco energéticos, que de pocos cuantos muy energéticos, por ejemplo, correspondientes a la radiación ultravioleta. Esto explica que el gráfico decaiga en longitudes de onda cortas. La proposición de Planck reproduce el máximo en el gráfico de intensidad emitida versus longitud de onda, tal como se muestra en la Figura \(\PageIndex{2}\). Por último, explica el corrimiento en la posición del máximo hacia menores longitudes de onda (frecuencias mayores) al incrementar la temperatura. En síntesis, la teoría de Planck ajustó precisamente los datos experimentales, donde la física clásica fallaba.
Cuando propuso esta hipótesis radical, Planck no pudo explicar porqué la energía estaba cuantizada. Inicialmente, su hipótesis solo explicaba un set de datos experimentales -los del cuerpo negro. Si la cuantización era observada en un gran número de fenómenos distintos, entonces se convertiría en ley. A su vez, una teoría debía ser desarrollada para explicar dicha ley. Con el correr del tiempo, la hipótesis de Planck fue la semilla de donde germinó la física moderna.
El efecto fotoeléctrico
Solo cinco años más tarde, la hipótesis de Planck sobre la cuantización fue utilizada para explicar un segundo fenómeno conflictivo para la física clásica. Cuando ciertos metales son expuestos a radiación, los electrones son despedidos de la superficie (Figura \(\PageIndex{3}\)). Esto se conoce como efecto fotoeléctrico. La física clásica predice que el número de electrones eyectados y su energía cinética dependen solo de la intensidad de la luz, no de su frecuencia.
Experimentalmente se encuentra que, bajo cierta frecuencia del haz de luz que incide sobre el metal, no hay electrones eyectados. Por otro lado, sobre dicha frecuencia, se emiten electrones con energía cinética proporcional a la frecuencia; también se encuentra que, a mayor intensidad del haz, más electrones son eyectados.
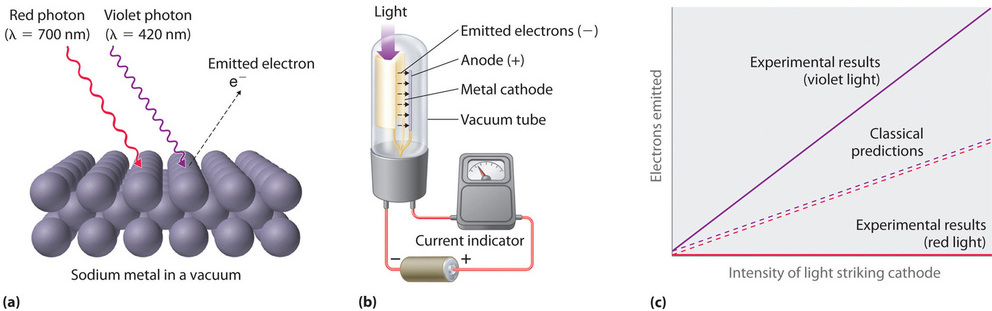
Figura \(\PageIndex{3}\): El efecto fotoeléctrico (a) Irradiar la superficie metálica con fotones de energía suficiente, se produce la eyección de electrones del metal. (b) Una fotocélula utilizada en el experimento. Cuando el fotón impacta en el cátodo metálico, se emiten electrones y son atraídos hacia el ánodo, resultando en un flujo de corriente. Se utilizan como sensores, por ejemplo, en puertas automáticas. Cuando pasa una persona el haz se interrumpe y la puerta se abre. (c) En contraste a las predicciones de la física clásica, no se despiden electrones si la energía del fotón es menor al umbal de energía (\(E_o\)). tal como la luz roja en el ejemplo. La energía del fotón ultravioleta, en cambio, está sobre \(E_o\). En este caso, el número de electrones emitidos es proporcional a la intensidad de la luz.
Albert Einstein (1879-1955; Premio Nobel, 1921) rápidamente notó que la hipótesis de Planck sobre la cuantización de la energía radiante podía explicar el efecto fotoeléctrico. Asumió que la energía radiante llega a la supeficie del metal en fotones (o cuantos de energía radiante), cada uno con una energía dada por la ecuación \ref{6.2.1}. Einstein postuló que cada metal ejerce una atracción electrostática específica sobre sus electrones (\(E_o=\nu_o\)), y que debe ser superada para lograr eyectarlo. Si fotones con energía menor que Eo impactan la superficie del metal, no habrá emisión de electrones, independientemente de la intensidad de la luz. Si un fotón con energía mayor a Eo impacta el metal, parte de su energía se utiliza para vencer el potencial atractivo y el exceso se convierte en la energía cinética del electrón eyectado:
\[ \begin{align} \text{ energía cinética electrón eyectado} &=E-E_{o} \nonumber \\[5pt] &=h\nu -h\nu _{o} \nonumber \\[5pt] &=h\left ( \nu -\nu _{o} \right ) \label{6.2.2} \end{align}\]
Cuando un metal es irradiado con luz de energía mayor al umbral (Eo), el número de electrones emitidos es proporcional a la intensidad del haz incidente, que corresponde al número de fotones por centímetro cuadrado. Pero la energía cinética del fotón emitido no depende de la intensidad, y es proporcional a la frecuencia del haz. En resumen, la frecuencia se traduce en velocidad, la intensidad en número.
Las ideas de Einstein, a diferencia de las previas basadas en la física clásica, explicaban los datos experimentales.

Figure \(\PageIndex{4}\): Luz roja emitida por láser de Helio/Neón, utilizada para leer código de barra. La emisión es a 632.8 nm. Hoy en día, se utilizan diodos láser más pequeños y baratos.
Albert Einstein (1879–1955)
En 1900 Einstein trabajaba en la oficina de patentes Suiza de Berna. Nación en Alemania y en su niñez sus padres y profesores estaban preocupados de que tuviera problemas en desarrollarse. El trabajo en la oficina de patentes era un servicio simple y de poca demanda, pero permitió a Einstein pasar mucho tiempo leyendo y pensando en física.

En 1905, el 'año milagroso', publicó cuatro papers que revolucionaron la física. Uno en la teoría especial de la relatividad, otro en el principio de equivalencia de masa y energía, un tercero en movimiento Browniano, y el último sobre el efecto fotoeléctrico, por el cual recibió el Premio Nobel en 1921. La teoría de la relatividad y la equivalencia materia-energía todavía eran controversiales en aquel tiempo.
El postulado de Planck y Einstein de que la energía estaba cuantizada era similar a la descripción de Dalton sobre los átomos. Ambas teorías se basaban en la existencia de bloques de construcción: átomos en un caso, cuantos de energía en el otro. El trabajo de Planck y Einstein sugirió una conexión entre la naturaleza cuantizada de la energía y las propiedades de átomos individuales.
ejemplo \(\PageIndex{1}\)
Un láser de rubí emite longitud de onda roja a 694.3 nm (Figura \(\PageIndex{4}\)). ¿Cuál es la energía en joules de un único fotón?
Dato: longitud de onda.
Pregunta por: energía de un único fotón.
Estrategia:
Utilizar ecuación \ref{6.1.2} y ecuación \(\ref{6.2.1}\) para calcular la energía en joules.
Solución:
La energía de un único fotón está dada por E= hν = hc/λ.
ejercicio \(\PageIndex{1}\)
Un generador de rayos-x, como los utilizados en hospitales, emite radiación con longitud de onda de 1.544 Å.
- ¿Cuál es la energía en joules de un único fotón?
- ¿Cuánto más energético es un fotón de rayo-x que uno emitido po el láser de rubí?
- Respuesta a
-
\(1.287 \times 10^{-15}\; J/fotón\)
- Respuesta b
-
4497 veces
Resumen
El bloquesde construcción fundamentale de la materia es el átomos, de la energía el cuanto. El fenómeno de radiación del cuerpo negro, la radiación emitida por cuerpos calientes, no pudo ser explicado por la física clásica. Max Planck postuló que la energía estaba cuantizada y podía ser emitida o absorbida solo en múltiplos enteros de cierta unidad de energía (muy pequeña), denominada cuanto. La energía de un cuanto es proporcional a la frecuencia de la radiación; la constante de proporcionalidad es una constante fundamental, la constante de Planck (h). Einstein utilizó el concepto de Planck sobre la cuantización de la energía para explicar el efecto fotoeléctrico, esto es, la eyección de electrones por partículas de luz de cierta energía.
Colaboradores
Modified by Joshua Halpern (Howard University)
Traducción de Santiago Miranda (Universidad Nacional de La Plata)

