2.2: ¿Cuántos electrones? Estadísticas de Fermi-Dirac

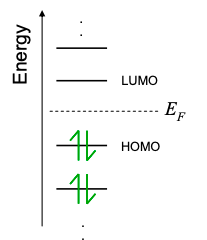
En la sección anterior, determinamos los niveles de energía permitidos de una partícula en un pozo cuántico. Cada nivel de energía y su función de onda asociada se conoce como un “estado”. El principio de exclusión Pauli prohíbe que múltiples electrones idénticos ocupen el mismo estado simultáneamente. Por lo tanto, uno podría esperar que cada estado en el conductor pueda poseer solo un solo electrón. Pero los electrones también poseen espín, una característica mecánica puramente cuántica. Para cualquier orientación dada, el espín de un electrón puede medirse para ser +1/2 o -1/2. Nos referimos a estos electrones como spin up o spin down.

Los electrones de giro son diferentes a los electrones de giro. Así, el principio de exclusión permite dos electrones por estado: uno spin up y otro spin down.

A continuación, si tuviéramos que añadir electrones a un material que de otro modo sería “vacío”, y luego dejáramos solos a los electrones, en última instancia ocuparían su distribución de equilibrio.

Como se podría imaginar, en equilibrio, los estados de energía más bajos se llenan primero, y luego los siguientes más bajos, y así sucesivamente. A T = 0K, el llenado de estado procede de esta manera hasta que no quedan electrones. Así, a T = 0K, la distribución de electrones viene dada por

\[ f(E,\mu)=u(\mu - E) \nonumber \]

donde u es la función de paso de unidad. La ecuación 2.2.1 muestra que todos los estados se llenan por debajo de una energía característica\(\mu\), conocida como el potencial químico. Cuando se usa para describir electrones, el potencial químico también se conoce a menudo como la Energía Fermi,\(E_{F}=\mu\). Aquí, seguiremos una convención que utiliza\(\mu\) para simbolizar el potencial químico de un contacto, y\(E_{F}\) para describir el potencial químico de un conductor.

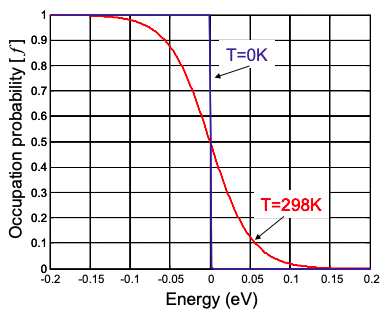
El equilibrio requiere que los electrones tengan la misma temperatura que el material que los sostiene. A temperaturas más altas, la energía térmica adicional puede excitar algunos de los electrones por encima del potencial químico, desdibujando la distribución en la Energía Fermi; ver Figura 2.2.1.

Para temperaturas arbitrarias, los electrones son descritos por la distribución de Fermi Dirac:

\[ f(E,\mu)=\frac{1}{1+\text{exp}[(E-\mu)/kT]} \nonumber \]

Obsérvese que la Ecuación 2.2.2 reduce a la Ecuación 2.2.1 en el límite T = 0K. En el Fermi Energy,\(E=E_{F}=\mu\), los estados están medio llenos.

Figura\(\PageIndex{1}\): La probabilidad de ocupación de electrones a dos temperaturas diferentes. El potencial químico en este ejemplo es\(\mu =0\).

Es conveniente relacionar la Energía Fermi con el número de electrones. Pero para ello, necesitamos conocer la distribución energética de los estados permitidos. Esto suele resumirse mediante una función conocida como la densidad de estados (DOS), que representamos por g (E). Habrá mucho más sobre el DOS más adelante en esta sección. Se define como el número de estados en un conductor por unidad de energía. Se utiliza para calcular el número de electrones en un material.

\[ n=\int^{+\infty}_{-\infty} g(E)f(E,\mu)dE \nonumber \]

Figura\(\PageIndex{2}\): A la izquierda, se muestra una posible estructura energética para una molécula a T = 0K. Se puede pensar en una molécula como un pequeño punto que confina electrones en todas direcciones. Así, al igual que el cuántico 1 dimensional bien estudiado anteriormente, los niveles de energía, o estados, en una molécula son discretos. Para una molécula cada estado a menudo se describe como un orbital molecular. Debajo de la energía Fermi, cada orbital molecular, contiene dos electrones, uno de giro hacia arriba y otro de giro hacia abajo. Representamos estos electrones con flechas apuntando hacia arriba y hacia abajo. El orbital molecular más alto ocupado se abrevia frecuentemente como HOMO. El orbital molecular desocupado más bajo es el LUMO.