2.4: Metales y Aisladores

Última actualización
Guardar como PDF

Page ID: 84389

Marc Baldo
Massachusetts Institute of Technology via MIT OpenCourseWare

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Los metales son buenos conductores; una pequeña diferencia entre\(F^{+}\) y\(F^{-}\) produce una gran diferencia entre el número de electrones en\(+k_{z}\) y\(-k_{z}\) estados. Esto es posible si las bandas están parcialmente llenas en equilibrio.

Si no hay electrones entre\(F^{+}\) y\(F^{-}\), entonces el material es un aislante y no puede conducir carga. Esto ocurre si las bandas están completamente vacías o completamente llenas en equilibrio. Aún no nos hemos encontrado con una banda que pueda llenarse por completo. Estos vendrán más tarde en la clase.

Así, para calcular la corriente en un material, debemos determinar el número de electrones en estados que se encuentran entre los niveles cuasi Fermi. A menudo es conveniente aproximar la Ecuación 2.2.2 al calcular el número de electrones en un material. Hay dos casos limitantes:

límite degenerado:\(E_{F}-E_{C} \ggkT\).

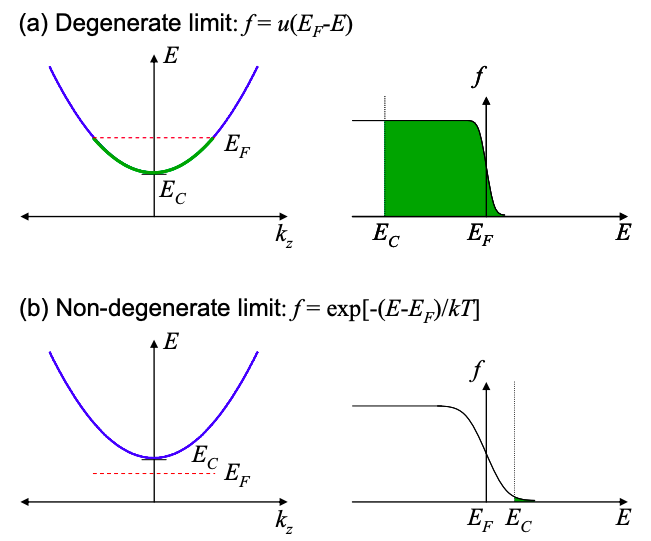
Como se muestra en la Figura 2.4.1 (a), aquí la parte inferior de la banda\(E_{C}\),, es mucho menor que la energía Fermi,\(E_{F}\), y la función de distribución es modelada por un paso unitario:

\[ f(E) = u(E_{F}-E) \nonumber \]

límite no degenerado:\(E_{C}-E_{F} \ggkT\).

Como se muestra en la Figura 2.4.1 (b), aquí\(E_{C} \geq E_{F}\) y la función de distribución reduce a la distribución de Boltzmann:

\[ f(E) = \text{exp}[-(E-E_{f})/kT] \nonumber \]

Captura de pantalla 2021-04-15 a las 21.23.03.png — Figura\(\PageIndex{1}\): Dos casos limitantes al calcular el número de electrones en un material. (a) Si\(E_{F}\) está dentro de una banda, entonces la desdefinición térmica de la distribución de electrones no es significativa, y simplemente podemos integrar hasta\(E_{F}\). Este es el llamado caso degenerado. (b) Por otra parte, si los estados llenados se deben únicamente a la excitación térmica anterior\(E_{F}\), la fracción de llenado disminuye exponencialmente. Este es el límite no degenerado.