3.7: Cálculo de Corriente
- Page ID
- 84343
Moderemos la corriente neta en cada interfaz contacto/molécula como la suma de dos componentes: la corriente de contacto, que es la corriente que fluye hacia la molécula, y la corriente de molécula, que es la corriente que fluye fuera de la molécula.
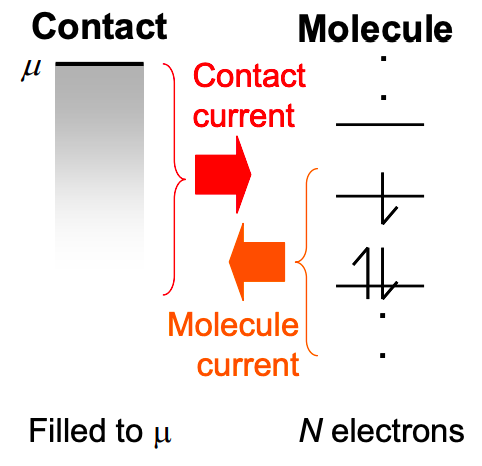
La corriente de contacto
Esta corriente es el número de estados disponibles en la molécula llenada por segundo. Los electrones en el contacto se llenan hasta su potencial químico. No pueden saltar a estados de mayor energía en la molécula. El número total de electrones que se pueden transferir es simplemente igual al número de estados.
En el contacto de origen, obtenemos
\[ N_{S} = \int^{\infty}_{-\infty}g(E-U)f(E,\mu_{S})dE \nonumber \]
donde\(g(E-U)\) es la densidad molecular de los estados desplazada por el cambio potencial neto. Del mismo modo, si en el contacto de drenaje entonces el número de electrones\(N_{D}\),, ese nivel podría transferirse es
\[ N_{D} = \int^{\infty}_{-\infty}g(E-U)f(E,\mu_{D})dE \nonumber \]
Definamos la velocidad de transferencia en los contactos de origen y drenaje como\(1/\tau_{S}\) y\(1/\tau_{D}\), respectivamente. Entonces las corrientes de contacto son
\[ I^{C}_{S} = q\frac{N_{S}}{\tau_{S}},\ \ \ I^{C}_{D} = -q\frac{N_{D}}{\tau_{D}} \nonumber \]
Tenga en cuenta que hemos definido el flujo de electrones fuera de la fuente y hacia el drenaje como positivo.
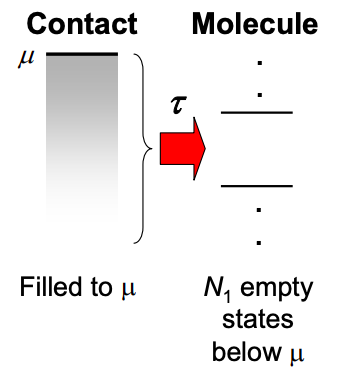
La corriente de la molécula
Ahora bien, si agregamos electrones a la molécula, estos electrones pueden fluir de nuevo al contacto, creando una corriente que se opone a la corriente de contacto. La corriente de la molécula es el número de electrones transferidos de la molécula al contacto por segundo.
Por lo tanto, las corrientes de la molécula en la fuente y los contactos de drenaje son
\[ I^{M}_{S} = -q\frac{N}{\tau_{S}},\ \ \ I^{M}_{D} = q\frac{N}{\tau_{D}} \nonumber \]
donde nuevamente hemos definido el flujo de electrones fuera de la fuente y hacia el drenaje como positivo.
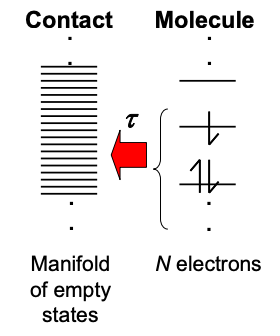
De las ecuaciones (3.7.3) y (3.7.4) la corriente neta en el contacto de la fuente es
\[ I_{S} = \frac{q}{\tau_{S}}(N_{S}-N) \nonumber \]
y la corriente neta en el contacto de drenaje es
\[ I_{D} = \frac{q}{\tau_{D}}(N-N_{D}) \nonumber \]
Tenga en cuenta que hemos asumido que las tasas de transferencia dentro y fuera de cada contacto son idénticas. Por ejemplo, definamos\(\tau^{M}_{S}\) como la vida útil de un electrón en la molécula y\(1/\tau^{C}_{S}\) como la velocidad de transferencia de electrones desde el contacto fuente. Quizás no sea obvio eso\(\tau^{M}_{S}=\tau^{C}_{S}\), pero el examen de las corrientes de entrada y salida en equilibrio confirma que debe ser así. Cuando la unión fuente-molécula está en equilibrio, no fluye corriente. De las Ecuaciones (3.6.6), (3.6.7) y (3.7.1), tenemos\(N_{S} =N\). Así, pues\(I_{S} =0\) debemos tener\(\tau_{1}^{M} = \tau_{1}^{C}\).
Equiparar las corrientes en Ecuaciones. (3.7.5) y (3.7.6) da\(^{†}\)
\[ I=q\int^{\infty}_{-\infty}g(E-U)\frac{1}{\tau_{S}+\tau_{D}} (f(E,\mu_{S})-f(E,\mu_{D}))dE \nonumber \]
y
\[ N = \int^{\infty}_{-\infty} g(E-U)\frac{\tau_{D}f(E,\mu_{S})+\tau_{S}f(E,\mu_{D})}{\tau_{S}+\tau_{D}}dE \nonumber \]
La dificultad para evaluar la corriente es que depende de U y por lo tanto de N. Pero la Ecuación (3.7.8) no es una solución de forma cerrada para N, ya que el lado derecho también contiene una dependencia de N vía U. Excepto en casos simples, esto significa que debemos resolver iterativamente para N, y luego usar la solución para obtener I. Esto se discutirá con mayor detalle en los problemas que acompañan a esta Parte.
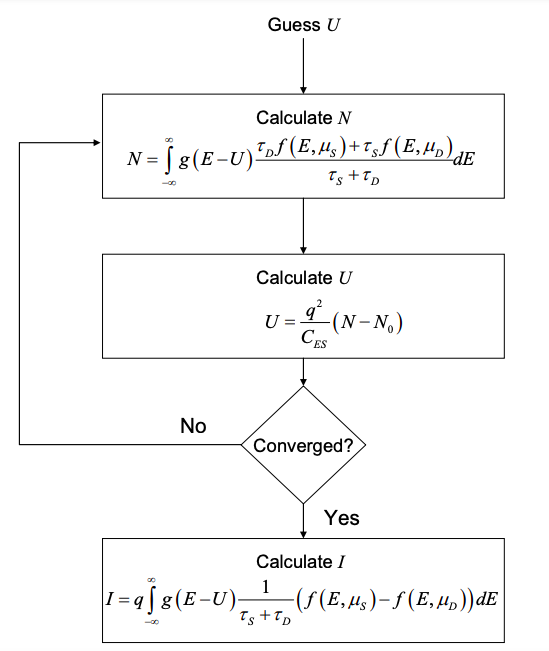
\(^{†}\)F. Zahid, M. Paulsson, y S. Datta, “La conducción eléctrica en moléculas”. En Semiconductores Avanzados y Nanotécnicas Orgánicas, ed. H. Korkoc. Prensa Académica (2003).


