5.5: Capítulo 5 Tareas

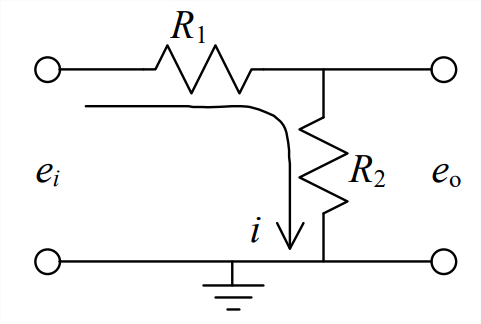
1. El circuito en serie simple representado gráficamente a continuación es un divisor de voltaje, que es ampliamente utilizado en aplicaciones prácticas. Demostrar que la relación de salida a entrada de voltaje es\[\frac{e_{o}}{e_{i}}=\frac{R_{2}}{R_{1}+R_{2}} \nonumber \]

   

2. Dos capacitores están dispuestos en serie, como se muestra a continuación.

   

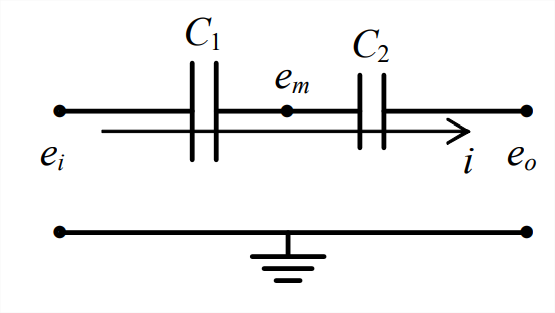
   1. Use la ecuación de corriente-voltaje para condensador\(C_1\) para mostrar eso\(\dot{e}_{m}=\dot{e}_{i}-\frac{i}{C_{1}}\), donde los\(e\) s son los voltajes indicados en el dibujo y\(i\) es la corriente.
   2. Utilice el resultado de la parte 5.2.1 y la ecuación de corriente-voltaje del condensador para el condensador con el\(C_2\) fin de derivar una fórmula algebraica para la capacitancia en serie equivalente\(C_{e q}\) (en términos de\(C_1\) y\(C_2\)) en la ecuación\(i=C_{e q}\left(\dot{e}_{i}-\dot{e}_{o}\right)\).
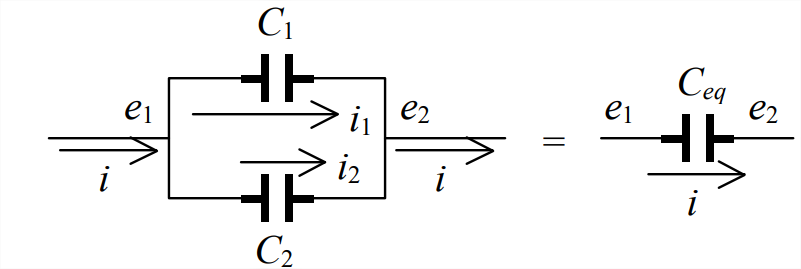
3. Dados condensadores\(C_1\) y\(C_2\) dispuestos en paralelo, como se muestra a continuación, encontrar la capacitancia única equivalente\(C_{e q}\).

   

4. El circuito simple representado gráficamente a continuación es un filtro ^de paso alto RC de primer orden.

   

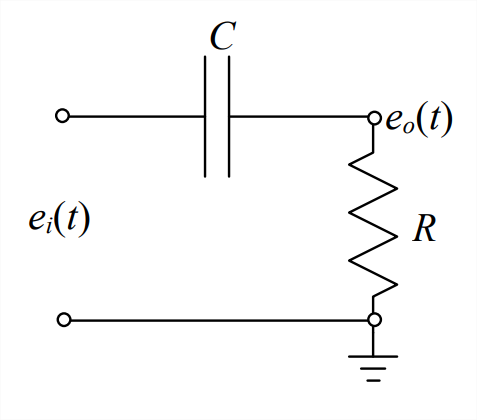
   1. Utilice la continuidad de corriente y las fórmulas que relacionan la corriente con la diferencia de voltaje para resistencias y condensadores para derivar con todo detalle la siguiente ODE con dinámica del lado derecho (RHS), que gobierna el voltaje de salida\(e_{o}(t)\) en términos de voltaje de entrada\(e_{i}(t)\):\[\dot{e}_{o}+\frac{1}{\tau_{1}} e_{o}=\dot{e}_{i}, \tau_{1}=R C \nonumber \] Explique por qué este circuito es considerado como un análogo eléctrico exacto del filtro de paso alto amortiguador-resorte de serie mecánica descrito en la Figura 3.7.4 y la Ecuación 3.7.6.
   2. Para la respuesta de frecuencia, el voltaje de entrada es\(e_{i}(t)=E_{i} \cos \omega t\) y el voltaje de salida de estado estacionario es\(e_{o}(t)=E_{o} \cos (\omega t+\phi)\). ^{Utilice la ecuación gobernante de la parte 5.4.1 para derivar las ecuaciones algebraicas para FRF del filtro paso alto de primer orden: la relación de magnitud\(E_{o}(\omega) / E_{i}\) y la fase\(\phi(\omega)\) (en radianes) como funciones de la frecuencia de excitación\(\omega\).} (respuesta parcial:\(E_{o}(\omega) / E_{i}=\omega \tau_{1} / \sqrt{1+\left(\omega \tau_{1}\right)^{2}}\).) Supongamos que\(R\) = 40 k\(\Omega\) y\(C\) = 0.25\(\mu\) F (recordar que\(\mu\) = 10 ^-6). Calcular la frecuencia de rotura\(f_{b}=1 /\left(2 \pi \tau_{1}\right)\) en Hz. Para tener alguna sensación sobre el funcionamiento de un filtro de paso alto, calcule la relación de magnitud FRF\(E_{o}(\omega) / E_{i}\) para las relaciones de frecuencia de conducción\(f / f_{b}\) = 0.01, 0.1, 1, 10 y 100. (Ver también tarea Problema 4.4.)
   3. Supongamos que el voltaje de entrada es una rampa\(e_{i}(t)=e_{r}\left(t / t_{r}\right) H(t)\),, donde\(e_{r}\) es un voltaje de referencia y\(t_{r}\) es un tiempo de referencia tal que\(e_{i}\left(t_{r}\right)=e_{r}\). Para IC\(e_{o}(0)\) = 0 voltios, resolver la ODE gobernante de la parte 5.4.1 para la ecuación algebraica para\(e_{o}(t)\) en términos de los parámetros algebraicos dados. Tenga en cuenta que la derivada de la tensión de entrada en este caso es una función de paso,\(\dot{e}_{i}(t)=\left(e_{r} / t_{r}\right) H(t)\).
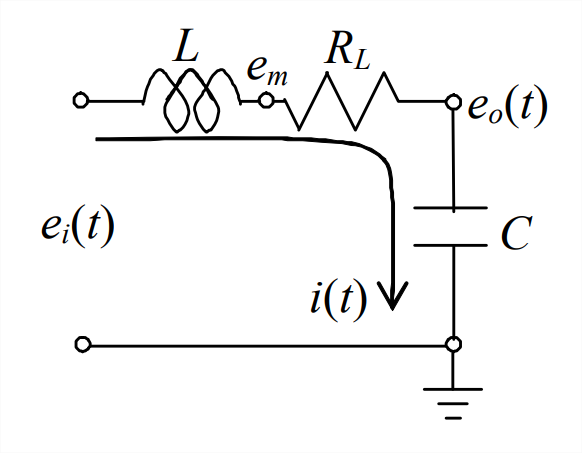
5. El circuito dibujado a continuación es una combinación en serie de una fuente de voltaje\(e_{i}(t)\), una bobina (que tiene inductancia\(L\) y resistencia\(R_L\)) y un condensador\(C\); esto se conoce como\(LRC\) circuito. El voltaje de entrada se aplica en el tiempo\(t\) = 0, momento en el cual hay un voltaje distinto de cero en el condensador,. Aplicar la ley de voltaje de Kirchhoff, como en el Ejemplo de Electricidad 5.2.4, y mostrar que la ecuación para corriente\(i(t) \text { is } L \frac{d i}{d t}+R_{L} i+\frac{1}{C} \int_{\tau=0}^{\tau=t} i(\tau) d \tau=e_{i}(t)-e_{o}(0)\).

   

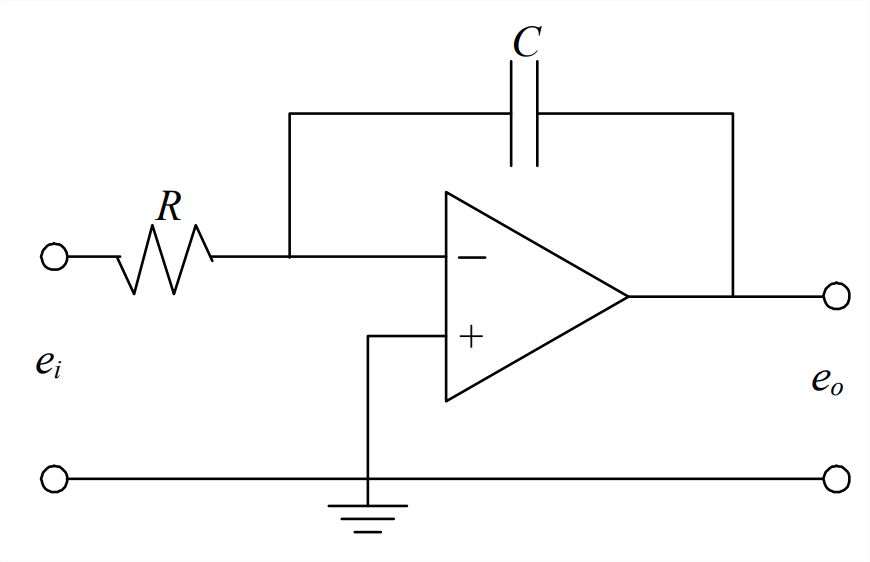
6. Para el circuito op-amp representado gráficamente a la derecha, un integrador, derivar la ecuación algebraica para la función de transferencia entre voltajes de entrada y salida,\(T F(s)=\frac{L\left[e_{o}(t)\right]}{L\left[e_{i}(t)\right]}\). Supongamos que no hay carga inicial en el condensador en el tiempo\(t\) = 0. Para simplificar la derivación, aplicar regla Ecuación 5.3.7. ¹

   

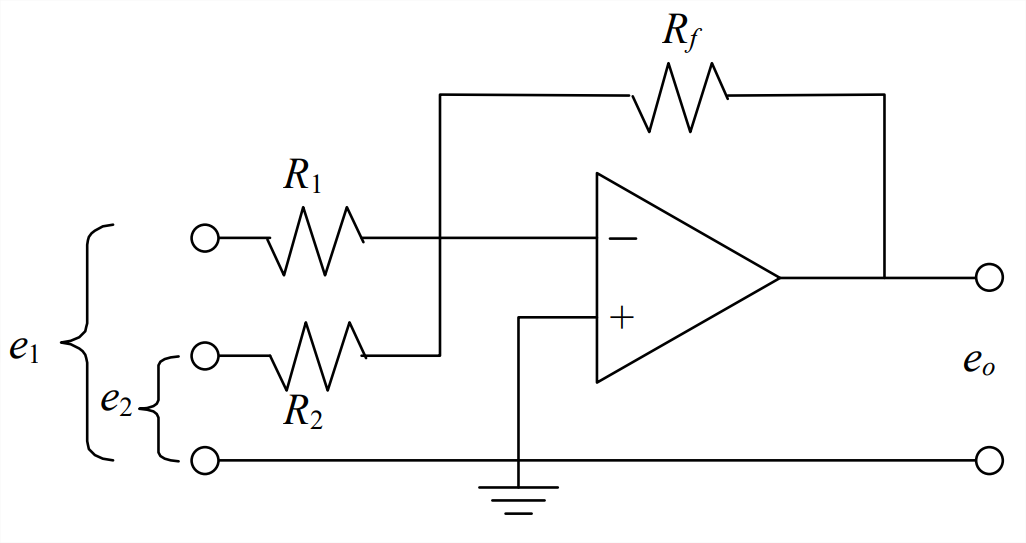
7. Para el circuito op-amp representado gráficamente a continuación, un amplificador inversor sumador, derivar la ecuación algebraica para el voltaje de salida\(e_{o}(t)\) en términos de resistencias\(R_1\),\(R_2\), y\(R_f\), y voltajes de entrada\(e_1(t)\) y\(e_2(t)\). Para simplificar la derivación, aplicar regla Ecuación 5.3.7.

   

8. 1. Para el circuito op-amp representado gráficamente a continuación, un amplificador no inversor, derivar la ecuación algebraica para el voltaje de salida\(e_{o}(t)\) en términos de resistencias\(R_1\) y\(R_2\), y voltaje de entrada\(e_{i}(t)\). Para simplificar la derivación, aplicar regla Ecuación 5.3.7.

      

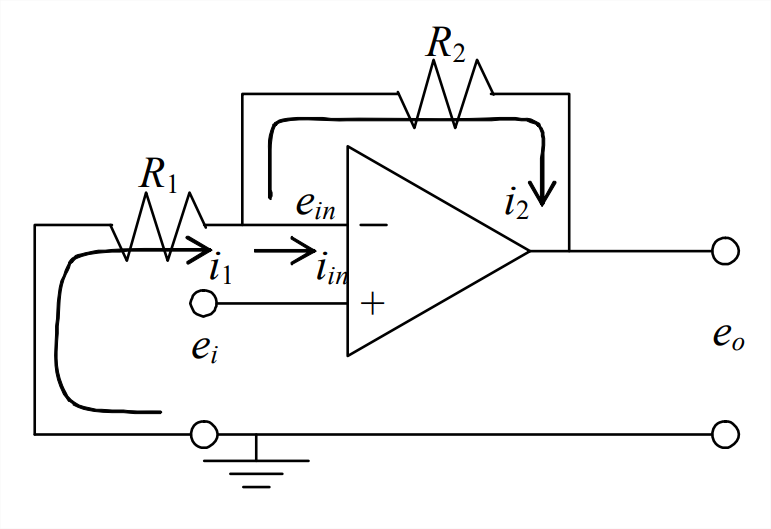
   2. Supongamos que\(e_{i}\) = 1.6 V,\(R_1\) = 5 k\(\Omega\), y\(R_2\) = 15 k\(\Omega\). Determinar los valores de\(e_{i n}\) (en V),\(i_{i n}\) (en miliamperios, mA),\(i_1\) (en mA),\(i_2\) (en mA) y\(e_o\) (en V).
9. El siguiente dibujo del circuito muestra un amplificador inversor, de la Figura 5.3.2, y, en la entrada del amplificador, una resistencia variable con un contacto deslizante, a menudo llamado limpiaparabrisas. La resistencia máxima útil de la resistencia variable es\(R_p\); sin embargo, al mover el limpiaparabrisas a lo largo de la superficie de la resistencia (ajustado girando un dial o un tornillo), podemos conectar entre\(e_{i}\) y\(e_{i m}\) cualquier porción\(\alpha R_{p}\), donde\(0 \leq \alpha \leq 1\). El propósito de esta configuración de circuito particular es permitir que la constante de ganancia del amplificador se ajuste continuamente a cualquier valor entre cero y\(R_{f} / R_{i}\), en lugar de restringirse al valor\(R_{f} / R_{i}\) de la Ecuación 5.3.5. Su asignación es derivar las siguientes ecuaciones de salida a entrada de voltaje:\[\frac{e_{i m}}{e_{i}}=\frac{(1-\alpha)}{1+\alpha(1-\alpha) \frac{R_{p}}{R_{i}}} \Rightarrow \frac{e_{o}}{e_{i}}=-\frac{(1-\alpha) \frac{R_{f}}{R_{i}}}{1+\alpha(1-\alpha) \frac{R_{p}}{R_{i}}} \nonumber \] En su derivación, no descuide la corriente a tierra a través del lado de la resistencia variable con resistencia\((1-\alpha) R_{p}\). Para aplicaciones en computadoras analógicas electrónicas (ver la nota al pie de página de la tarea Problema 5.6), esta disposición de una resistencia variable se llama potenciómetro de ajuste de coeficientes o simplemente una olla para abreviar.

   

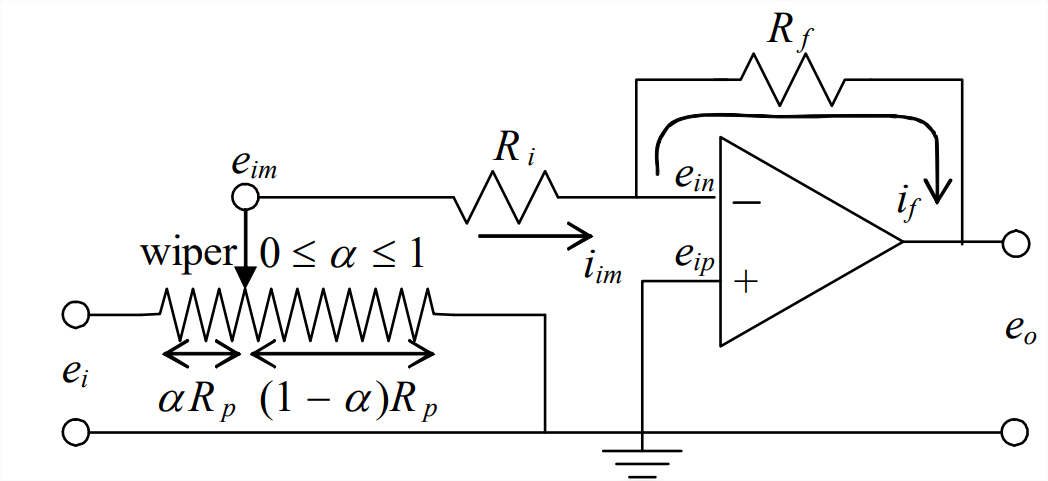
   Amplificador inversor con potenciómetro de ajuste de coeficientes

10. El circuito representado gráficamente a continuación consta de dos etapas, cada etapa se construye alrededor de un amplificador operacional.

    

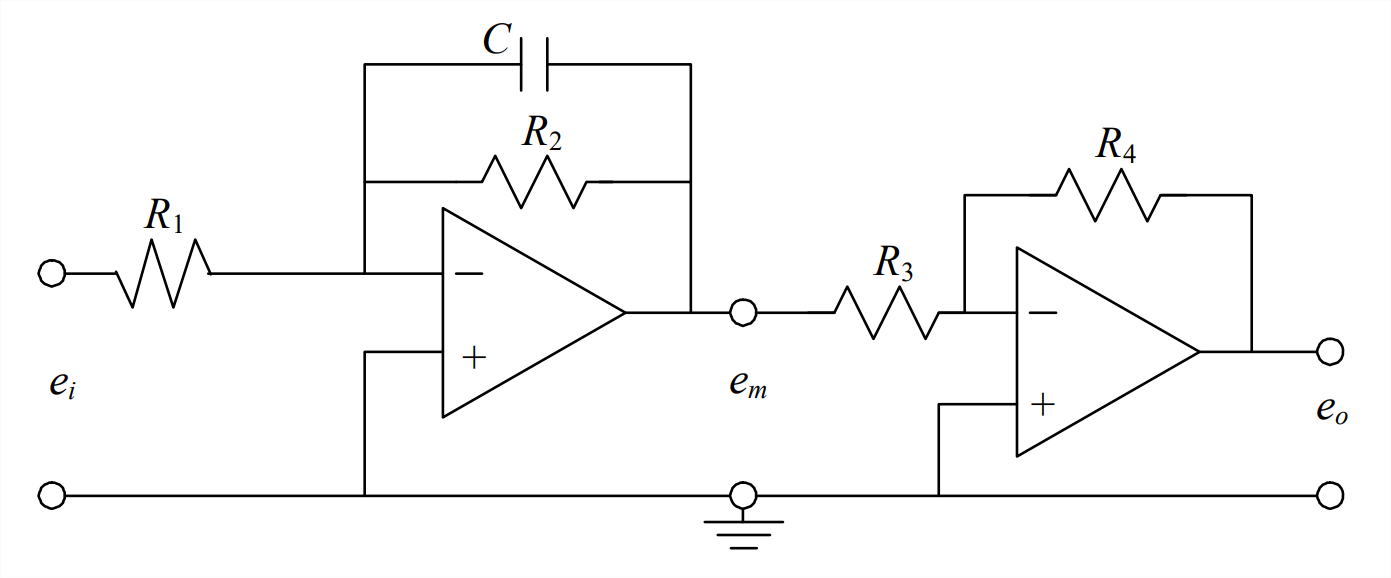
    1. Derive de la etapa izquierda el siguiente ODE para voltaje entre etapas\(e_{m}(t)\):\[\dot{e}_{m}+\frac{1}{R_{2} C} e_{m}=-\frac{1}{R_{1} C} e_{i} \nonumber \]
    2. Combine el resultado de la parte 5.10.1 con el efecto de la etapa derecha para mostrar que la ODE para voltaje de salida\(e_{o}(t)\) es\(\dot{e}_{o}+\frac{1}{R_{2} C} e_{o}=\frac{R_{4}}{R_{3}} \frac{1}{R_{1} C} e_{i}\). (Nota: Este circuito es esencialmente la computadora analógica electrónica (ver la nota al pie de página a la tarea Problema 5.6) para resolver el estándar estable de 1 er ^orden ODE Ecuación 3.4.8,\(\dot{x}+\left(1 / \tau_{1}\right) x=b u(t)\). \(e_{i}(t)\)El voltaje de entrada es análogo a la entrada estándar\(u(t)\), el voltaje de salida\(e_{o}(t)\) es análogo a la respuesta, la constante\(\tau_{1}=R_{2} C\) de tiempo y la constante)\(b=\frac{R_{4}}{R_{3}} \frac{1}{R_{1} C}\).
11. El circuito representado gráficamente en la siguiente página es la forma básica e ideal del controlador electrónico analógico proporcional-integral (PI), uno de los temas del Capítulo 15. (En la práctica, se requiere una gran cantidad de refinamiento y acondicionamiento electrónico para producir un circuito que se comporte incluso cerca de lo ideal). La señal de voltaje de entrada es\(e_{e}(t)\), la tensión intermedia entre las dos etapas es\(e_{m}(t)\), y la tensión de salida del controlador PI es\(w(t)\).

    

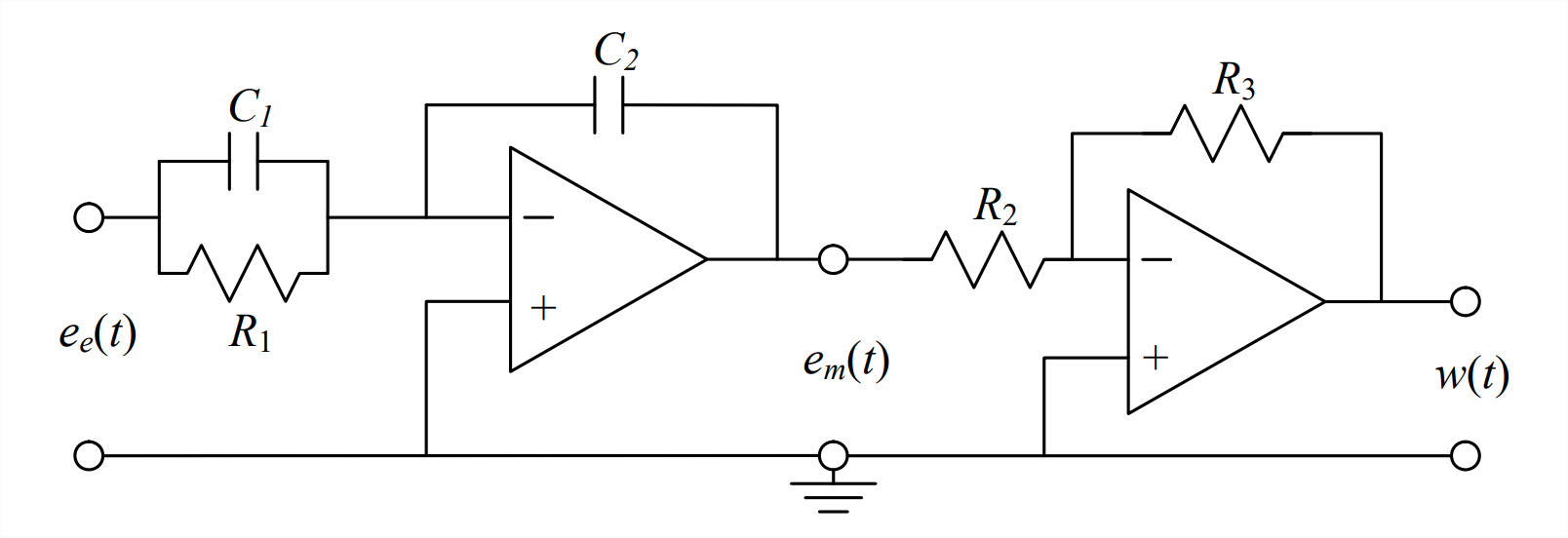
    1. Mediante la aplicación de los métodos de análisis de circuitos descritos en el Capítulo 5, se muestra que la ODE que relaciona la salida del controlador PI\(w(t)\) a la entrada\(e_{e}(t)\), expresada en términos de los parámetros del condensador y la resistencia del diagrama del circuito, es:\[\dot{w}=\frac{R_{3} C_{1}}{R_{2} C_{2}}\left(\dot{e}_{e}+\frac{1}{R_{1} C_{1}} e_{e}\right) \nonumber \]
    2. Derive la función de transferencia del controlador PI\(T F(s) \equiv \frac{\left.L[w(t)]\right|_{w_{0}=0}}{\left.L\left[e_{e}(t)\right]\right|_{e_{e}=0}}\), expresada en términos de los parámetros del condensador y la resistencia del diagrama del circuito.

¹ Este integrador parece sencillo en papel, pero el diseño de un integrador real que funcione correctamente es difícil, requiriendo costosos componentes de precisión y muchos refinamientos sutiles del circuito básico. Los integradores basados en este circuito son componentes esenciales de la computadora electrónica analógica (EAC), un elegante instrumento que data de la década de 1940 para resolver ODEs acopladas, pero que ahora ha sido reemplazado casi por completo por computadoras digitales. El conjunto de cuatro volúmenes de 1961 de Fifer es probablemente la descripción más completa de todos los tipos de computadoras analógicas; el libro de texto de 1967 de Peterson incluye material de instrucción estándar sobre EAC; y el artículo de Lang en 2000 es una discusión interesante y más moderna de los EAC.