7.1: Forma estándar para sistemas de segundo orden sin amortiguar y frecuencia natural
- Page ID
- 84666
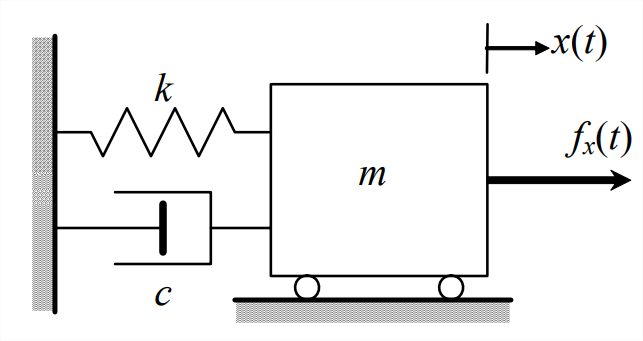
Para el sistema masa-amortiguador-resorte (\(m\)\(c\)- -\(k\)) de la Figura\(\PageIndex{1}\), la ecuación ODE de movimiento 3.7.1 derivada de la 2ª ley de Newton, con el uso del FBD en la Figura 3.7.1, es
\[m \ddot{x}+c \dot{x}+k x=f_{x}(t)\label{eqn:7.1} \]
Si descuidamos la amortiguación estableciendo\(c \dot{x}= 0\) la ecuación\(\ref{eqn:7.1}\), entonces tenemos un sistema ideal (no real) de masa-resorte (\(m\)-\(k\)) sin amortiguar. Este sistema pasivo no amortiguado no es totalmente realista porque cada sistema físico pasivo está afectado con algún tipo y grado de disipación de energía, aunque muy pequeño en algunos sistemas 1. Sin embargo, es útil estudiar el sistema sin amortiguar porque revela algunas características fundamentales importantes de los sistemas de segundo orden. De la ecuación\(\ref{eqn:7.1}\), la ODE para el\(k\) sistema\(m\) - es:
Usemos Ecuación\(\ref{eqn:7.2}\) para desarrollar la forma estándar que se aplicará a los sistemas de segundo orden sin amortiguar de manera más general. Primero, definimos algebraicamente la frecuencia natural de vibración no amortiguada como la raíz cuadrada positiva del cociente de los valores de rigidez y masa (ambos positivos en la mayoría de los sistemas pasivos):
\[\omega_{n} \equiv \sqrt{\frac{k}{m}}\label{eqn:7.3} \]
La frecuencia natural es muy importante físicamente: se muestra en la siguiente sección que un sistema de segundo orden no amortiguado tiende a vibrar (oscilar, pulsar, temblar, temblar,...) periódicamente a\(\omega_{n}\) radianes de frecuencia circular por segundo. A continuación, definimos la cantidad de entrada estándar
\[u(t) \equiv \frac{1}{k} f_{x}(t)\label{eqn:7.4} \]
Así que ahora definimos\(x(t)\) como representar cualquier cantidad de salida apropiada (no necesariamente solo posición como en la Figura\(\PageIndex{1}\)), y reescribimos Ecuación\(\ref{eqn:7.2}\) en forma estándar (estándar en este libro, al menos, y sobre todo estándar en literatura de ingeniería):
\[\ddot{x}+\omega_{n}^{2} x=\omega_{n}^{2} u(t)\label{eqn:7.5} \]
De Ecuación\(\ref{eqn:7.5}\) vemos que la entrada\(u(t)\) tiene exactamente las mismas dimensiones físicas que la salida\(x(t)\). De hecho, podemos identificarnos\(u(t)\) como la salida pseudo-estática,\(x_{p s}(t)\); es decir, si\(x(t)\) varía lo suficientemente lentamente que\(\ddot{x}\) es insignificante en comparación con\(\omega_{n}^{2} x\), entonces la ecuación ODE se\(\ref{eqn:7.5}\) reduce a una ecuación algebraica simple\(\omega_{n}^{2} x \approx \omega_{n}^{2} u(t)\),, cuya solución es la respuesta pseudo-estática,\(x(t)=u(t) \equiv x_{p s}(t)\). Esta respuesta se llama pseudo-estática porque no es necesariamente estática (constante en el tiempo), sino que varía lo suficientemente lenta como para que la segunda derivada de la respuesta sea despreciable.
Ejemplo\(\PageIndex{1}\)
Probablemente hayas visto el péndulo de un reloj de abuelo. El péndulo simple ideal es muy similar: hay una sacudida de masa\(m\) unida al extremo inferior de una varilla de longitud\(\ell\), estando el extremo superior de la varilla soportado en bisagra sin fricción\(H\). Asumimos que la varilla es rígida y tiene un momento inercial insignificante. El péndulo cuelga hacia abajo y oscila de lado a lado con ángulo\(\theta(t)\) en el plano del papel, sujeto a la aceleración de la gravedad,\(g\). Para la completitud, incluimos un agente que puede imponer sobre el péndulo un momento aplicado arbitrario\(M(t)\) sobre\(H\). Debido a que descuidamos la inercia de la varilla, la inercia rotacional del péndulo alrededor\(H\) es\(J=m \ell^{2}\).
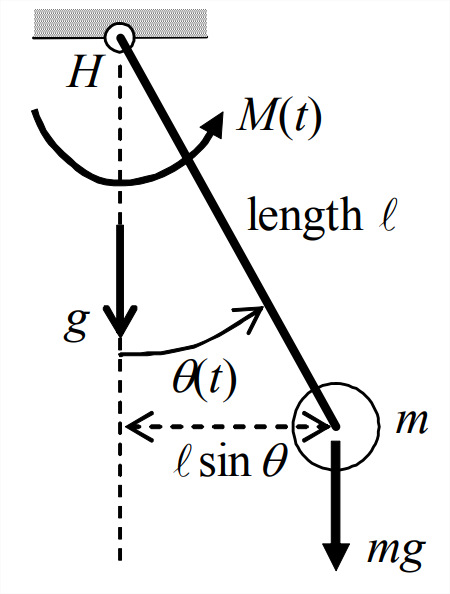
La segunda ley de Newton para la rotación sobre\(H\) es
\[\Sigma(\text { all applied moments about } H)=J \times\text{ rotational acceleration }=m \ell^{2} \ddot{\theta} \nonumber \]
\[\Rightarrow \quad M(t)-m g \times \ell \sin \theta=m \ell^{2} \ddot{\theta} \Rightarrow m \ell^{2} \ddot{\theta}+m g \ell \sin \theta=M(t) \nonumber \]
Debido al\(\sin\theta\) término, la ODE exacta es no lineal. Sin embargo, consideremos solamente pequeños ángulos rotacionales\(|\theta|<\approx 10^{\circ}\), para lo cual\(\sin \theta \cong \theta\) en radianes. Esta restricción linealiza la ODE:
\[m \ell^{2} \ddot{\theta}+m g \ell \theta=M(t) \Rightarrow \ddot{\theta}+\frac{g}{\ell} \theta=\frac{g}{\ell} \frac{M(t)}{m g \ell} \Rightarrow \ddot{\theta}+\omega_{n}^{2} \theta=\omega_{n}^{2} u(t) \nonumber \]
En la forma estandarizada de la ODE linealizada, la frecuencia natural es\(\omega_{n}=\sqrt{g / \ell}\), y la cantidad de entrada estándar (también la respuesta pseudo-estática) es\(u(t)=\theta_{p s}(t)=M(t) / m g \ell\). Para el péndulo en pequeños ángulos rotacionales, el término\(m g \ell \theta\) es el momento restaurador que se opone al movimiento desde la posición de equilibrio estático no forzado,\(\theta\) = 0; esencialmente, la gravedad juega el papel de un resorte de rotación. Ver tarea Problema 7.4 para otro interesante sistema rotacional pendular, un globo que porta una canasta.


