15.1: Definiciones iniciales y control PID

Última actualización
Guardar como PDF

Page ID: 84602

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

La figura\(\PageIndex{1}\) es un diagrama de bloques funcional general que representa muchos sistemas de control de ingeniería. El término operación de error de entrada se puede definir en el contexto de este diagrama: una sola cantidad de salida se retroalimenta y se diferencia de la cantidad de entrada de configuración del operador, y la señal de error es manipulada matemáticamente por un controlador, también llamado procesador de control o filtrar, de tal manera que se produzca un control efectivo. El controlador generalmente consiste en circuitos electrónicos analógicos y/o un procesador digital.

Figura\(\PageIndex{1}\): Diagrama de bloques funcionales del sistema de control general mediante operaciones de error de entrada. (Copyright; autor vía fuente)

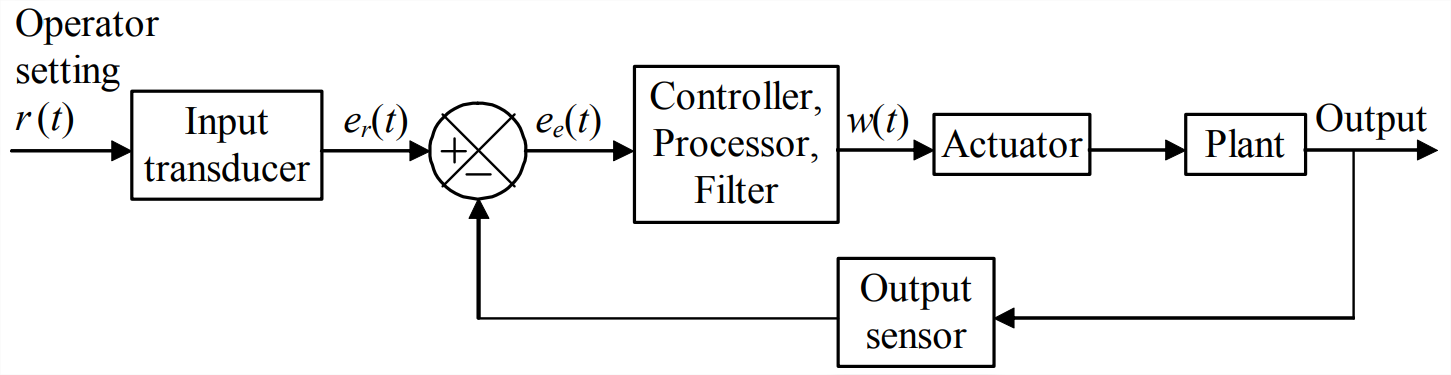
El control proporcional-integral-derivado (PID) es una clase de operaciones de error de entrada que se usa ampliamente en la industria. Deje\(e_{e}(t)\) ser la señal de voltaje de error que se ingresa al controlador y\(w(t)\) sea la tensión de salida del controlador, como se muestra en la Figura\(\PageIndex{1}\). Las operaciones matemáticas realizadas por un controlador PID ideal se describen mediante la ecuación

\[w(t)=P\left[e_{e}(t)+b_{i} \frac{1}{\tau_{i}} \int_{t=0}^{\tau=t} e_{e}(\tau) d \tau+b_{d} \tau_{d} \frac{d e_{e}}{d t}(t)\right]\label{eqn:15.1} \]

Las constantes físicas en la ecuación\(\ref{eqn:15.1}\) son ganancia proporcional\(P\), constante de tiempo integral y constante\(\tau_{i}\) de tiempo derivada\(\tau_{d}\). Cada una de las constantes binarias\(b_{i}\) y\(b_{d}\) tiene valor adimensional 1 o 0, dependiendo de si se incluyen o no acciones integrales y/o derivadas en el control. Determinar cuáles deben ser estas constantes para una aplicación en particular es una parte importante del proceso de diseño de control. Para encontrar la función de transferencia del controlador PID ideal, definimos las transformaciones de Laplace\(L\left[e_{e}(t)\right] \equiv E_{e}(s)\) y\(L[w(t)] \equiv W(s)\). Tomando la transformación Laplace de Equation\(\ref{eqn:15.1}\) proporciona la función de transferencia de controlador -PID ideal:

\[\frac{W(s)}{E_{e}(s)}=P\left[1+b_{i} \frac{1}{\tau_{i} s}+b_{d} \tau_{d} s\right]\label{eqn:15.2} \]

Consideraremos en los ejemplos tres subconjuntos de control PID que son de uso común: para el control proporcional (P), solo\(\ref{eqn:15.2}\) se usa el primer término dentro de los paréntesis de Ecuaciones\(\ref{eqn:15.1}\) y, por lo tanto\(b_{i}=b_{d}=0\); para el control proporcional-integral (PI), solo se utilizan los términos primero y segundo, por lo que \(b_{i}=1\)y\(b_{d}=0\); y para el control proporcional-derivado (PD), sólo se utilizan los términos primero y tercero, así\(b_{i}=0\) y\(b_{d}=1\).

Figura\(\PageIndex{2}\): Controlador electrónico analógico PI. (Copyright; autor vía fuente)

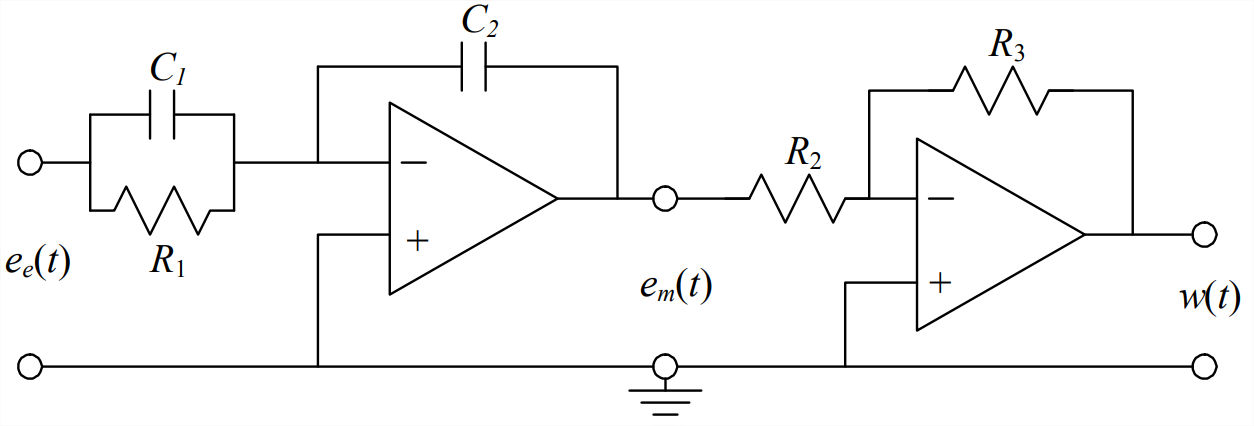
Para hacer más concreto el concepto de control PI, por ejemplo, la Figura\(\PageIndex{2}\) representa un circuito eléctrico analógico específico que, en principio, actúa como un controlador PI ideal. (En la práctica, se requiere una gran cantidad de refinamiento y acondicionamiento electrónico para producir un circuito que se comporte incluso cerca de lo ideal). Al aplicar los métodos de análisis de circuitos descritos en el Capítulo 5 (tarea Problema 5.11), podemos demostrar que las constantes PI (\(b_{i}=1\)y\(b_{d}=0\)) en Ecuaciones\(\ref{eqn:15.1}\) y\(\ref{eqn:15.2}\), expresadas en términos de los parámetros de circuito de la Figura\(\PageIndex{2}\), son:

\[P=\frac{R_{3} C_{1}}{R_{2} C_{2}}, \quad \tau_{i}=R_{1} C_{1}\label{eqn:15.3} \]

El diseño detallado de los controladores PID implica una gran cantidad de arte de ingeniería, así como ciencia de ingeniería, y se ha desarrollado extensamente; véase, por ejemplo, Ogata, 2001, Capítulo 10. El presente capítulo es solo una introducción al control PID, por lo que no profundizaremos en los detalles del diseño, sino que exploraremos algunas de las características más generales de los tipos de control P, PI y PD en el contexto de ejemplos relativamente simples.