16.7: Capítulo 16 Tarea

Última actualización
Guardar como PDF

Page ID: 84583

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Examine cualquiera de las siguientes ecuaciones características que se asignen, utilizando los criterios de Routh para determinar si todas sus raíces tienen partes reales negativas para que los sistemas asociados sean positivamente estables.
1. \(p-3=0\)
2. \(2 p+11=0\)
3. \(p^{2}+2 p+8=0\)
4. \(2 p^{2}-9 p+29=0\)
5. \(2 p^{3}+4 p^{2}+4 p+12=0\)
6. \(p^{3}+6 p^{2}+12 p+8=0\)
7. \(p^{4}-p^{3}+7 p^{2}+p-8=0\)
Considere el diagrama de bloques conceptual del sistema de bucle cerrado de Laplace a continuación, con dos parámetros del sistema posiblemente variables,\(K\) y\(Q\). Escriba la ecuación para la función de transferencia de bucle cerrado. A continuación, ampliar el polinomio denominador (característico) y aplicar los criterios de estabilidad de Routh para escribir todas las relaciones de desigualdad algebraica que involucran\(K\) y\(Q\) (en general) que deben satisfacerse para que el sistema sea positivamente estable. (No se preocupe por las unidades de\(K\) y\(Q\), sólo asuma que son consistentes.) Calcular el rango\(K\) para el cual el sistema es estable positivamente para cualquiera de los siguientes casos que se asigne: (a)\(Q = −0.5\) y\(+0.5\); (b)\(Q = −1.0\) y\(+1.0\); (c)\(Q = −1.5\) y\(+1.5\).

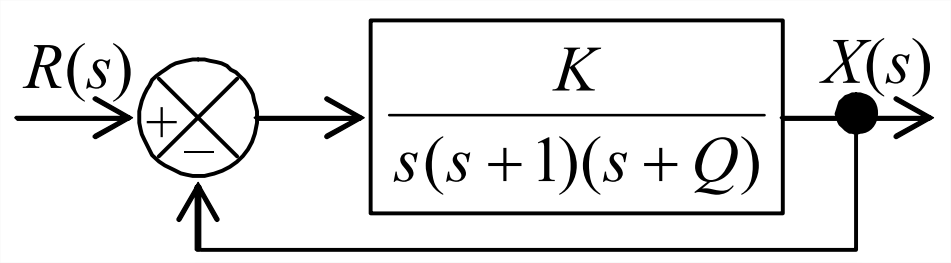
Figura\(\PageIndex{1}\) (Copyright; autor vía fuente)
Considera la ecuación característica\(p^{2}+2 C p+K=0\). \(m\)Siendo la masa positivo-definida, esta es la ecuación característica del sistema estándar de masa-amortiguador-resorte descrito por la ecuación de movimiento\(m \ddot{x}+c \dot{x}+k x=f_{x}(t)\), pero con la notación\(C \equiv c /(2 m)\) y\(K \equiv k / m\). Las raíces de esta ecuación polinómica de ^2º grado son los polos de la función de transferencia del sistema. Supongamos que la constante de amortiguación\(C=6\) sec ^-1, y que desea evaluar las características de estabilidad del sistema para diferentes valores de rigidez constante\(K\) seg ^-2. Considere primero los valores no negativos de\(K\). ¿Para qué valor positivo\(K \equiv K_{c}\) es crítico el amortiguamiento y para qué valores tienen las raíces polinómicas\(K \equiv K_{c}\)? (Definición: si el amortiguamiento es positivo pero menor que crítico, entonces las raíces son complejas, correspondientes a la respuesta de condición inicial que es oscilación modulada por una envolvente exponencial en descomposición; si, por otro lado, el amortiguamiento es igual o mayor que crítico, entonces las raíces son reales negativas, correspondientes a la respuesta monótona exponencialmente decayente de la condición inicial.) ¿Para qué valores son\(K = 0\) las raíces\(K=2 K_{c}\)? Mostrar cada una de estas raíces marcando grandes \(\times\)en las posiciones correctas en una gráfica de\(p\) plano complejo [\(x\)-eje es\(\operatorname{Re}(p)\),\(y\) -eje es\(\operatorname{Im}(p)\), ambos en sec ^-1]; etiquetar los ejes y la escala lineal de los ejes, la misma escala en ambos ejes, como en el gráfico de MATLAB Figura 16.8. Explicar concisamente qué calidad de las raíces indica que el sistema es estable para todos los valores de\(K>0\). Ahora calcule los valores de las raíces para una rigidez negativa, digamos\(K=-3 K_{c}\), y marque esas raíces en su gráfica\(p\) -plano. Desde las raíces para una rigidez negativa, ¿qué se puede afirmar de manera concluyente sobre la estabilidad del sistema para todos los valores negativos de\(K\)? Indica claramente en tu\(p\) -plano grafica los loci de raíces a medida que K aumenta de\(-3 K_{c}\) a 0, luego de 0 a\(+K_{c}\), luego de\(K_{c}\) a\(2 K_{c}\), y finalmente para\(K_{c}>2 K_{c}\). ¿Hay un punto de ruptura en tus loci de raíces; si es así, ¿para qué valor de\(K\)?
Las siguientes ecuaciones características se expresan en formas total o parcialmente factorizadas. Para las ecuaciones que se le asignen, encuentre el orden\(n\) del sistema asociado, resuelva por las raíces y marque sus ubicaciones con grandes \(\times\)en un boceto del\(p\) plano complejo, y determine si el sistema es estable o inestable; dé la (s) razón (s) para su conclusión.
1. \((p-4)(p+3)(p+4)(p+5)=0\)
2. \(p(p+2)\left(p^{2}-6 p+34\right)=0\)
3. \((p+1)(p+3-j 5)(p+3+j 5)=0\)
4. \((p+3)\left(p^{2}+2 p+2\right)\left(p^{2}+4 p+20\right)=0\)
El diagrama de bloques de Laplace a la derecha representa un sistema similar al de las Figuras 16.3.1 y 16.3.2: es un rotor amortiguado con retroalimentación de posición que es filtrado de paso bajo. Pero el filtro de paso bajo en este caso es de ^orden 2, mientras que el filtro de la Figura 16.3.2 es de ^primer orden. La función de transferencia de filtros en el diagrama de bloques es de la Ecuación 10.2.3: la frecuencia de interrupción de paso bajo\(\omega_{b}\) es la frecuencia natural no amortiguada, y\(\gamma\) es la relación de amortiguación viscosa del filtro. Especificamos el valor\(\gamma=1 / \sqrt{2}\); como se muestra en la gráfica de relación magnitud-respuesta de la Figura 10.2.1, para ello\(\gamma\), la atenuación de magnitud at\(\omega=\omega_{b}\) es\(1 / \sqrt{2}\) (igual que para un filtro de primer ^orden), y el roll-off de alta frecuencia es de dos décadas por cada década de incremento de frecuencia (dos veces más empinada que el roll-off de un filtro ^de primer orden). (Véase también la discusión de filtros paso bajo de ^segundo orden al final de la Sección 10.2.)

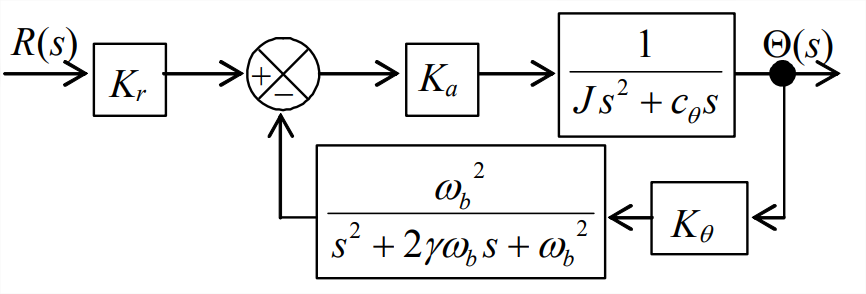
Figura\(\PageIndex{2}\) (Copyright; autor vía fuente)
1. Derivar del diagrama de bloques la ecuación algebraica para la función de transferencia de bucle cerrado,\(\operatorname{CLTF}(s) \equiv \Theta(s) / R(s)\) (en términos de los símbolos mostrados, sin números en esta etapa). De tu\(\operatorname{CLTF}(s)\), escribe la ecuación característica,\(\operatorname{Den}(p)=0\).
2. Utilizar los mismos valores que para los cálculos del Capítulo 16:\(\omega_{b}=300\) rad/s y\(c_{\theta} / J=100\) s ^-1, así como\(\gamma=1 / \sqrt{2}\). También como en el Capítulo 16, denotar el parámetro variable del sistema de control como\(\Lambda \equiv K_{a} K_{\theta} / J\). Utilice la operación raíz de MATLAB para calcular, imprimir y trazar los loci de raíces de este sistema en todo el rango de\(\Lambda\) valores para los que el sistema es positivamente estable. Su gráfica y salida numérica deben mostrar con al menos 2-3 cifras significativas de precisión cualquier punto de ruptura y los límites superior e inferior de estabilidad. Encuentre por ensayo y error el valor aproximado\(\Lambda\) para el cual el modo oscilatorio dominante de respuesta tiene la relación de amortiguación del sistema\(\zeta \approx 1 / \sqrt{2}\), y también calcular la constante de tiempo\(\tau_{2}\) y la frecuencia\(\omega_{d}\) para este valor de\(\Lambda\).
El diagrama de bloques de Laplace aquí representa un sistema para controlar la posición angular de un satélite en un plano. El bloque de error de entrada desconocido en la rama delantera del bucle es la función de transferencia de un compensador, que en este caso está diseñado para colocar un par de polos de bucle cerrado del sistema en\(2 \pi(-1 \pm j 1)\) s ^-1 en el\(p\) plano -plano, para un valor de parámetro de control\(\Lambda \equiv K_{c} K_{a} K_{\theta} / J\). Para estos polos, la frecuencia es\(f_{d}=\omega_{d} / 2 \pi=1\) Hz, y la relación de amortiguación viscosa es\(\zeta=1 / \sqrt{2}\).

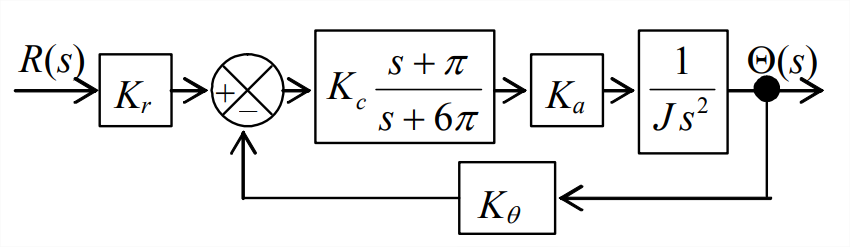
Figura\(\PageIndex{3}\) (Copyright; autor vía fuente)
1. Derivar del diagrama de bloques la ecuación algebraica para la función de transferencia de bucle cerrado\(\Theta(s) / R(s)\),, luego escribir la ecuación característica,\(\operatorname{Den}(p)=0\).
2. Utilice la operación raíz de MATLAB para calcular, imprimir y trazar los loci de raíces de este sistema sobre el rango de parámetros\(0 \leq \Lambda \leq 200\) s ^-2.
3. Utilice el método root-locus de Evans para determinar el valor numérico de\(\Lambda\) que produce polos\(2 \pi(-1 \pm j 1)\) s ^-1.
(Adaptado de Franklin, et al., 1991, Problema 5.25 en la página 347) El diagrama de bloques de Laplace del sistema de control de velocidad de una unidad de cinta magnética se muestra en la siguiente figura. La configuración del operador es la señal de voltaje de entrada\(e_{i n}(t)\), cuya transformada de Laplace es\(E_{i n}(s)\). Cada subsistema principal del sistema de control funciona como un sistema ^de primer orden. El subsistema que consiste en un amplificador de potencia y un actuador de par tiene sensibilidad variable\(K_{a}\) (N-m/V) y constante de tiempo\(\tau_{a}=1.0\) s. el accionamiento de cinta tiene inercia rotacional\(J = 4.0\) N-m por rad/s ² y constante de amortiguación viscosa de eje lubricado\(c_{\theta}=1.0\) N-m por rad/s; la salida de la unidad de cinta en esta aplicación es velocidad de rotación\(p(t)\) en rad/s [con transformada Laplace\(P(s)\)], no posición rotacional\(\theta(t)\). El sensor de velocidad de rotación en la rama de retroalimentación tiene sensibilidad\(K_{p}\) = 1.250 V por rad/s; este sensor es suficientemente lento en relación con los otros subsistemas que debemos dar cuenta de su constante de tiempo,\(\tau_{p}=0.5\) s.
1. Derivar la función de transferencia de bucle cerrado\(P(s) / E_{i n}(s)\), y luego mostrar que la ecuación característica de este sistema se puede expresar como\[\left(p+c_{\theta} / J\right)\left(p+\tau_{a}^{-1}\right)\left(p+\tau_{p}^{-1}\right)+\Lambda=0, \text { or } r_{1} e^{j \theta_{1}} \times r_{2} e^{j \theta_{2}} \times r_{3} e^{j \theta_{3}}=\Lambda \exp [j(\pm \pi, \pm 3 \pi, \ldots)] \nonumber \] donde se define el parámetro de control variable como\(\Lambda=K_{a} K_{p} /\left(J \tau_{a} \tau_{p}\right)\), con unidades de ^s-3.
2. Determine (a mano, no MATLAB) todos los polos de bucle abierto, todas las asíntotas (as\(\Lambda \rightarrow \infty\)) de los polos de bucle cerrado y las direcciones de salida de los loci raíz de los polos de bucle abierto a medida que\(\Lambda\) aumenta desde cero. Esboce en papel\(p\) cuadriculado un plano, e indique en él la información que determinó para este sistema. Consulte la Figura 16.6.2 para ver un ejemplo del tipo de diagrama que debería ser el suyo. Haz conjeturas educadas y dibuja en tu diagrama los formularios que crees que deberían tener los loci raíz.
3. A partir de la parte 16.7.1, cualquier punto en un locus de raíces debe satisfacer la igualdad de ángulo:\(\theta_{1}+\theta_{2}+ \theta_{3}=\pm \pi, \pm 3 \pi, \ldots\). Usa esta igualdad para escribir una ecuación trascendental que se pueda resolver para el polo de bucle cerrado\(j \omega_{d}\) en el límite superior de estabilidad\(\Lambda_{u b}\) de los loci oscilatorios complejos; tu ecuación incluirá funciones trigonométricas para los\(\theta_{i}\) ángulos que involucran\(\omega_{d}\) y los valores numéricos de los polos de bucle abierto. No es necesario que resuelvas la ecuación trascendental, pero puedes mostrar solo por sustitución que\(\omega_{d}=1.6583124\) s ^-1\(=\sqrt{11} / 2\) s ^-1 es la solución. Finalmente, nuevamente usando el resultado de la parte 16.7.1, resuelve para el valor\(\Lambda_{u b}=r_{1} \times r_{2} \times r_{3}\); tu ecuación incluirá términos para las\(r_i\) magnitudes que involucran\(\omega_{d}\) y los valores numéricos de los polos de bucle abierto. [Nota: también podrías resolver esta parte aplicando los criterios de Routh, las ecuaciones 16.3.5 y 16.3.6, para calcular\(\Lambda_{u b}\), luego sustituyendo de\(\Lambda_{u b}\) nuevo en la ecuación característica para resolver\(p=j \omega_{d}\).]
La función de transferencia de bucle abierto de un determinado sistema de control es\[G(s) H(s) \equiv O L T F(s)=\Lambda \frac{s^{2}+4 s+104}{(s+1)\left(s^{2}+2 s+26\right)} \nonumber \] donde\(\Lambda\) (con unidades s ^-1) es un parámetro variable con rango posible\(0 \leq \Lambda<+\infty\).
1. Determine (a mano, no MATLAB) todos los polos de bucle abierto y ceros de bucle abierto de este sistema, cualquier asíntota (as\(\Lambda \rightarrow \infty\)) de los polos de bucle cerrado y las direcciones de salida de los loci raíz de los polos de bucle abierto a medida que\(\lambda\) aumenta desde cero. Esboce en papel\(p\) cuadriculado un plano, e indique en él la información que determine para este sistema. Consulte la Figura 16.6.2 para ver un ejemplo del tipo de diagrama que debería ser el suyo. Sin embargo, mientras que la Figura 16.6.2 no muestra ningún ceros de bucle abierto, su diagrama debería; es tradicional marcar un cero de bucle abierto por un\(\text {O}\), así como un polo de bucle abierto está marcado por un\(\times\). Haz conjeturas educadas y dibuja en tu diagrama los formularios que crees que deberían tener los loci raíz.
2. Mostrar que la ecuación característica del sistema de bucle cerrado es\[p^{3}+(3+\Lambda) p^{2}+4(7+\Lambda) p+26(1+4 \Lambda)=0 \nonumber \] Aplicar los criterios de Routh, Ecuaciones 16.3.5 y 16.3.6,\(\Lambda\) para calcular límites y rangos de estabilidad; en particular, resolver una ecuación cuadrática en desconocido\(\Lambda\) para mostrar que dos de los límites son\(\Lambda_{1,2}=8 \pm \sqrt{49.5}\) s -1 = 0.964376 s ^-1 y 15.0356 s ^-1. Para interpretar la significancia de estos límites en relación con la estabilidad, se calcula la ecuación cuadrática para valores\(\Lambda\) ligeramente por encima y por debajo de estos dos límites. A continuación, sustituya los valores\(\Lambda_1\) y\(\Lambda_2\) vuelva\(p=j \omega_{d 2}\) a la ecuación característica como\(p=j \omega_{d 1}\) y para resolver para las frecuencias oscilatorias\(\omega_{d 1}\)\(\Lambda_1\) y\(\omega_{d 2}\) at y (\ Lambda_2\), respectivamente—habrá una parte real y una imaginaria de la ecuación que se puede resolver; calcular el\(\omega_{d 1,2}\) de la parte más fácil, luego simplemente sustituir ese valor de\(\omega_{d 1,2}\) en la parte más difícil para demostrar que también está satisfecho. ¿Cuál es el significado de\(\omega_{d 1,2}\) y\(\Lambda_{1,2}\) en su diagrama en la parte 16.8.1?
La ecuación característica de un determinado sistema LTI-SISO se puede expresar como\[1+G(p) H(p)=1+\Lambda \frac{p+1}{(p-1)(p+3)\left(p^{2}+2 p+2\right)}=0 \nonumber \] donde\(\Lambda\) es un parámetro de ganancia variable con rango posible\(0 \leq \Lambda<+\infty\).
1. Determine (a mano, no MATLAB) todos los polos de bucle abierto y el cero de bucle abierto de este sistema, todas las asíntotas (as\(\Lambda \rightarrow \infty\)) de los polos de bucle cerrado y las direcciones de salida de los loci raíz de los polos de bucle abierto a medida que\(\Lambda\) aumenta desde cero. Esboce en papel\(p\) cuadriculado un plano, e indique en él la información que determine para este sistema. Consulte la Figura 16.6.2 para ver un ejemplo del tipo de diagrama que debería ser el suyo. Sin embargo, mientras que la Figura 16.6.2 no muestra ningún ceros de bucle abierto, su diagrama debería; es tradicional marcar un cero de bucle abierto por un\(\text{o}\), así como un polo de bucle abierto está marcado por un\(\times\). Haz conjeturas educadas y dibuja en tu diagrama los formularios que crees que deberían tener los loci raíz.
2. Su información en la parte 16.9.1 debería sugerir que un locus de raíces está en el\(\operatorname{Re}(p)\) eje, comenzando desde un polo de bucle abierto en\(p=+1\) (for\(\Lambda=0\)) y terminando en un cero de bucle abierto en\(p=-1\) (for\(\Lambda \rightarrow \infty\)). Si eso es cierto, entonces este locus particular debe, para algún valor de\(\Lambda\) entre 0 y\(\inf\), cruzar el origen del\(p\) -plano de\(p > 0\) (inestable) a\(p < 0\) (estable). Tu tarea es expresar la ecuación característica en forma polar [a la manera de las Ecuaciones 16.5.4 - 16.5.7], usa esa forma para probar que el segmento\(-1 \leq p \leq+1\) del\(\operatorname{Re}(p)\) eje es o no es un locus, y, si lo es, encontrar el valor de\(\Lambda\) at\(p = 0\), el límite entre inestabilidad y estabilidad.
3. Su solución de la parte 16.9.2 debe indicar: hay un locus en el segmento\(-1 \leq p \leq+1\) del\(\operatorname{Re}(p)\) eje; y ese locus tiene raíces estables por\(\Lambda\) mayor que su valor at\(p = 0\). Por otro lado, su información de la parte 16.9.1 debería mostrar que hay un par de polos complejos conjugados de bucle abierto en el medio plano occidental estable; también debería sugerir que los loci que parten de esos polos complejos de bucle abierto (for\(\Lambda=0\)) luego proceden en dirección este a medida que\(\Lambda\) aumenta de cero, entonces, para algún valor positivo de\(\Lambda\), cruzar sobre el\(\operatorname{Im}(p)\) eje hacia el semiplano oriental inestable. Entonces, a medida que\(\Lambda\) aumenta de cero, un locus real de raíces de bucle cerrado pasa de ser inestable a estable, pero un par de loci conjugados complejos pasan de ser estables a inestables. Por lo tanto, debemos preguntarnos si existe algún rango\(\Lambda\) para el cual todos los loci están en el medio plano occidental y el sistema de bucle cerrado es estable? Quizás la mejor manera de responder a esta pregunta es usar los criterios de estabilidad de Routh. Considerar una ecuación característica general de ^4º orden:\(a_{1} p^{4}+a_{2} p^{3}+a_{3} p^{2}+a_{4} p+a_{5}=0\). El sistema asociado es estable si y sólo si se cumplen todas las condiciones siguientes (Ogata, 2001, páginas 275-277):
  * todos\(a_{i}>0, i=1,2,3,4,5\);
  
  *\(R_{2} \equiv a_{2} \times a_{3}-a_{1} \times a_{4}>0\);
  
  *\(R_{3} \equiv R_{2} \times a_{4}-a_{2}^{2} \times a_{5}>0\).
  
  Utilice los criterios de estabilidad de Routh para determinar el rango\(\Lambda\) para el cual el sistema de bucle cerrado es estable, si existe tal rango.
(adaptado de Nelson, 1989, Problema 7.7 en las páginas 222-223) El Wright Flyer 1903 por sí mismo era inherentemente inestable en movimiento longitudinal (paso acoplado y traslación vertical). Sin embargo, Wilbur y Orville Wright estabilizaron, apenas apenas, el sistema de avión + piloto al proporcionar suficiente autoridad de control con un canard y al desarrollar la habilidad de vuelo a través de una extensa experimentación y práctica con planeadores pilotados. Se formuló un modelo matemático ¹ del sistema, el diagrama de bloques de Laplace para el cual se muestra a continuación. La entrada al sistema es la actitud de tono comandada\(\theta_{c}(t)\), y la salida es la actitud de tono real\(\theta(t)\). La posición de canard incremental es\(\delta(t)\), para lo cual es la transformación de Laplace\(\Delta(s)\). La función de transferencia de canard-position to pitch-attitude incorpora tanto dinámica de cuerpo rígido como aerodinámica; el modelo estimado de esta función de transferencia es\[\frac{\Theta(s)}{\Delta(s)}=\frac{11.0(s+0.5)(s+3.0)}{\left(s^{2}+5.9 s-11.9\right)\left(s^{2}+0.72 s+1.44\right)}=\frac{11.0(s+0.5)(s+3.0)}{(s-1.589)(s+7.489)\left(s^{2}+0.72 s+1.44\right)} \nonumber \]

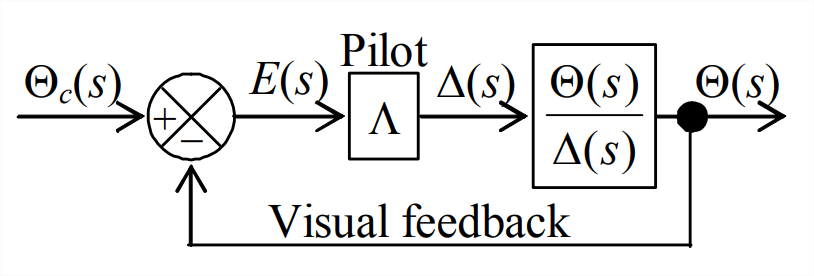
Figura\(\PageIndex{4}\) (Copyright; autor vía fuente)
1. Determine (a mano, no MATLAB) todos los polos de bucle abierto y ceros de bucle abierto de este sistema, todas las asíntotas (como ganancia piloto\(\Lambda \rightarrow \infty\)) de los polos de bucle cerrado, y las direcciones de salida de los loci raíz de los polos de bucle abierto a medida que\(\Lambda\) aumenta desde cero. Esboce en papel\(p\) cuadriculado un plano, e indique en él la información que determinó para este sistema. Consulte la Figura 16.6.2 para ver un ejemplo del tipo de diagrama que debería ser el suyo. Sin embargo, mientras que la Figura 16.6.2 no muestra ningún ceros de bucle abierto, su diagrama debería; es tradicional marcar un cero de bucle abierto por un\(\text{o}\), así como un polo de bucle abierto está marcado por un\(\times\).
2. Mostrar en detalle que la ecuación polinómica característica en la forma\(a_{1} p^{4}+a_{2} p^{3}+ a_{3} p^{2}+a_{4} p+a_{5}=0\), con todos los\(a_i\) coeficientes ya sea numéricos o combinaciones de números y ganancia piloto\(\Lambda\), viene dada por:\[p^{4}+6.62 p^{3}+(11 \Lambda-6.212) p^{2}+(38.5 \Lambda-0.072) p+(16.5 \Lambda-17.136)=0 \nonumber \]
3. Si deseamos en este punto programar en software el cálculo de loci de raíces, solo sabemos considerar\(0<\Lambda<\infty\); pero, sin más información, es difícil saber qué rango específico o incluso orden de magnitud de\(\Lambda\) ingresar inicialmente en los cálculos. Sin embargo, los criterios de estabilidad de Routh pueden proporcionar esa información adicional necesaria. Utilice los criterios de Routh [tarea Problema 16.9.3] y los coeficientes de la ecuación característica para evaluar la estabilidad absoluta del sistema Wright Flyer, determinando así cuantitativamente un rango candidato de\(\Lambda\) para su uso en el cálculo de loci de raíces. ² (Respuesta: para la estabilidad,\(\Lambda > 1.3096\))
4. Utilice la operación raíz de MATLAB para calcular, imprimir y trazar los loci de raíces de este sistema en un rango de\(\Lambda\) valores para los que el sistema es estable. A partir de la Ecuación 9.5.5, la relación\(\zeta=0.11\) de amortiguación viscosa del modo oscilatorio produce 50% de disminución de amplitud durante cada ciclo; muestre a partir de sus cálculos que\(\Lambda=3.24\) es la ganancia piloto más baja para la cual\(\zeta=0.11\), hasta una precisión de ingeniería razonable. De tus resultados para\(\Lambda=3.24\), ¿esperas que un modo oscilatorio sea dominante en la respuesta de tiempo, o un modo exponencial, o quizás una combinación de los dos?
5. Es de interés examinar con más detalle el caso de ganancia piloto\(\Lambda=3.24\), comenzando con la función de transferencia de bucle cerrado\(C L T F(s)\). Tenga en cuenta que esencialmente ya tenemos el denominador de\(C L T F(s)\): en la ecuación característica de la parte 16.10.2, solo reemplace\(p \rightarrow s\) y establezca\(\Lambda=3.24\). Mostrar que la función de transferencia de bucle cerrado, en la forma de la Ecuación 16.1.6, es:\[C L T F(s)=\frac{\Theta(s)}{\Theta_{c}(s)}=\frac{35.64\left(s^{2}+3.5 s+1.5\right)}{s^{4}+6.62 s^{3}+29.428 s^{2}+124.668 s+36.324} \nonumber \] Ahora aplique la operación de residuos de MATLAB (ver tarea Problema 2.15) para calcular los residuos y polos de\(C L T F(s)\), y escribir la forma de expansión de fracción parcial de\(C L T F(s)\). Tenga en cuenta que los polos encontrados en este paso deben coincidir con los de la parte 16.10.4 para\(\Lambda=3.24\).
6. Finalmente, considere una solución de respuesta forzada en el tiempo, con cero condiciones iniciales. Supongamos que el piloto ordena un pulso corto a la palanca de control de tono; representa este pulso aproximadamente con una función delta de Dirac (Sección 8.4):\(\theta_{c}(t)=I_{\theta} \delta(t)\), para la cual es la transformada de Laplace\(\Theta_{c}(s)=I_{\theta}\). Que la magnitud del impulso sea\(I_{\theta}=2\) grados-s. Utilice la forma de expansión de fracción parcial de la\(C L T F(s)\) parte 16.10.5 para derivar la ecuación para la respuesta de tono\(\theta(t)\) a esta excitación de control, y luego calcular y trazar esta respuesta transitoria en un intervalo de 15 segundos.
Sabemos por el Capítulo 16 que el proceso de cálculo y trazado de loci de raíces es útil en el análisis de la estabilidad del sistema de control; el objetivo de este problema es ilustrar otra aplicación importante de los loci de raíz: el análisis de la estabilidad de un sistema para el cual el potencial la retroalimentación desestabilizadora es natural e intrínseca, no diseñada por humanos. Los sistemas con esta característica a menudo se describen como autoexcitados (véase, por ejemplo, Den Hartog, 1956, Capítulo 7). El fenómeno particular que consideramos aquí, la respuesta dinámica aeroelástica de un plano aerodinámico de sección típica, incluido el aleteo inestable, se originó en la ingeniería aeronáutica, pero es relevante también para muchas otras aplicaciones de objetos generadores de fuerza que se sumergen dentro de fluidos en movimiento (p. hidrofilos, palas de turbinas eólicas y hélices). El perfil aerodinámico de sección típica se describe en la Sección 11.3, Ejemplos 11.3.2 y 11.3.3, y consideramos aquí la forma que se muestra a continuación, una superficie aerodinámica delgada simétrica, sin curvatura soportada por resortes en un túnel de viento, y sumergida dentro de una corriente de aire incompresible de densidad\(\rho\) y velocidad de flujo libre \(V\).

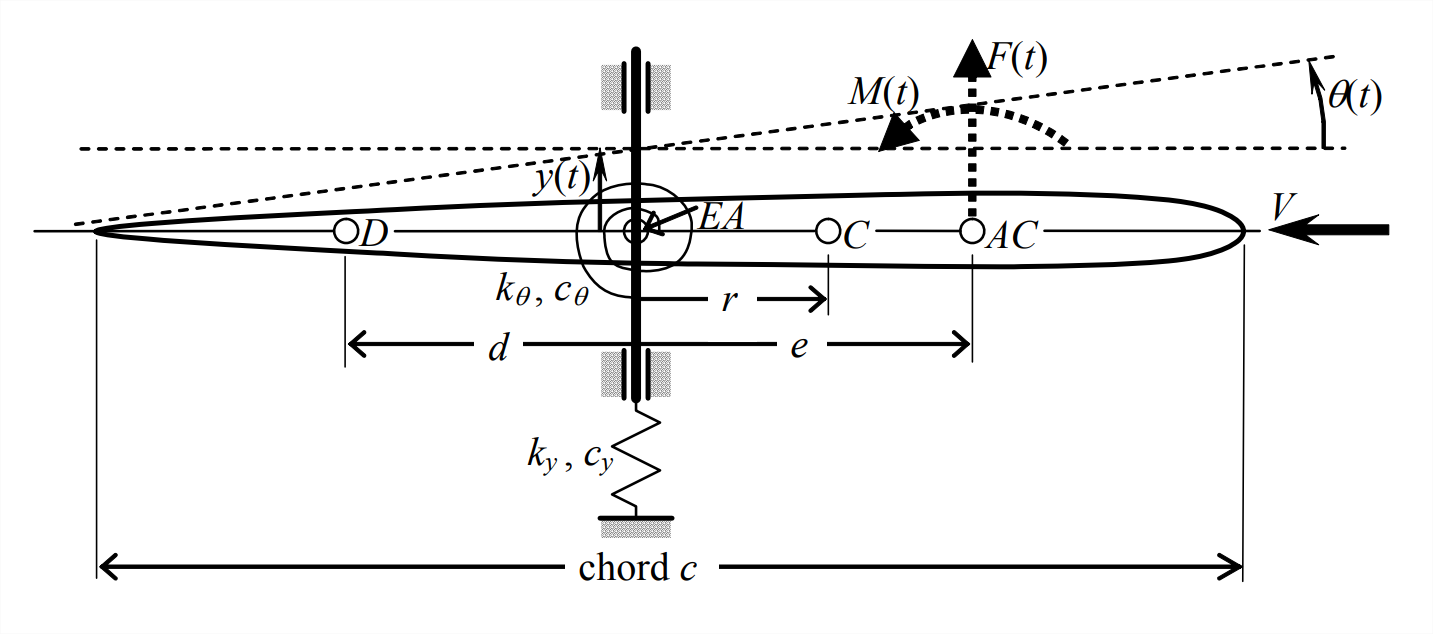
Figura\(\PageIndex{5}\) (Copyright; autor vía fuente)

Las ecuaciones dinámicas estructurales de movimiento con traslación vertical del centro de masa\(C\)\(y_{A C}(t)\), y el tono\(\theta(t)\) como grados de libertad (DOF) se derivan y se expresan en forma de matriz en la Ecuación 11.3.16. Sin embargo, un DOF de traslación vertical más apropiado para este problema es\(y_{E A}(t) \equiv y(t)\) del eje elástico\(EA\), como está etiquetado en la figura anterior; las ecuaciones de movimiento para DOF\(y(t)\) y\(\theta(t)\) se derivan en la tarea Problema 11.4 y se expresan a continuación, con la adición de una matriz de amortiguación que representa aproximadamente la disipación de energía dentro de los resortes (utilizando el modelo matemático de amortiguación de viscosidad descrito en el Apéndice B, Sección 19.5). \ [\ left [\ begin {array} {cc}
m & m r\\
m r & J_ {E A}
\ end {array}\ right]\ left [\ begin {array} {l}
\ ddot {y}\
\ ddot {\ theta}
\ end {array}\ right] +\ left [\ begin {array} {cc}
c_ {y} & 0\\
0 & c_ {\ theta}
\ end {array}\ derecha]\ left [\ begin {array} {l}
\ dot {y}\
\ dot {\ theta}
\ end {array}\ right] +\ left [\ begin {array} {cc}
k_ {y} & 0\\
0 & amp; k_ {\ theta}
\ end {array}\ right]\ left [\ begin {array} {l}
y\
\ theta
\ end {array}\ right] =\ left [\ begin {array} {c}
F (t)\
M (t) +F (t) e
\ end {array}\ right]\ label {eqn:p16.11.1}\] Suponemos que la fuerza de sustentación resultante aerodinámica y el momento (nariz hacia arriba positiva) se deben tanto a los movimientos de la sección típica misma (autoexcitación), como a fuentes como ráfagas que son independientes del movimiento, que denotamos como elevación\(F_{G}(t)\) y momento\(MG(t)\). No existe una teoría exacta y fácilmente aplicable de la aerodinámica inestable y dependiente del movimiento; por lo tanto, utilizamos aquí una de las muchas teorías aproximadas, la aerodinámica cuasisteady de Fung, 1955, páginas 191-193. En estas ecuaciones de sustentación inestable y momento, reemplazamos la pendiente de la curva de elevación de Fung por una superficie aerodinámica de envergadura infinita,\(C_{L \alpha}=2 \pi\) por radián, con un valor reducido del\(C_{L \alpha}\) que se aplica para un perfil aerodinámico de envergadura finita. Esto es apropiado para los parámetros numéricos específicos considerados a continuación en la parte 16.11.2, los cuales se eligen para representar una investigación experimental real de aeroelasticidad de sección típica. Dado que la presión dinámica es\(\bar{q}=1 / 2 \rho V^{2}\), es apropiado definir en las ecuaciones de Fung la constante\(K \equiv 1 / 2 \rho S(2 \pi) \rightarrow K \equiv 1 / 2 \rho S C_{L \alpha}\). Por lo tanto, el levantamiento aerodinámico resultante y el momento de levantamiento aerodinámico dependiente del movimiento e independiente del movimiento se escriben como: \[F(t)=\bar{q} S C_{L \alpha}\left(\theta-\frac{\dot{y}-d \dot{\theta}}{V}\right)+F_{G}(t)=K\left(V^{2} \theta-V \dot{y}+d V \dot{\theta}\right)+F_{G}(t)\label{eqn:P16.11.2a} \]\[M(t)=-\bar{q} S c \frac{\pi c}{8} \frac{\dot{\theta}}{V}+M_{G}(t)=-K \frac{\pi / 8}{C_{L \alpha}} c^{2} V \dot{\theta}+M_{G}(t)\label{eqn:P16.11.2b} \]
1. Sustituir las ecuaciones\(\ref{eqn:P16.11.2a}\) y\(\ref{eqn:P16.11.2b}\) en la ecuación\(\ref{eqn:P16.11.1}\), luego transponer los términos dependientes del movimiento desde el lado derecho al lado izquierdo para que las matrices de amortiguación y rigidez en la ecuación\(\ref{eqn:P16.11.1}\) se vuelvan más generales; por ejemplo, la matriz de rigidez estructural-más-aerodinámica se convierte en\ (\ left [\ begin {array} {cc}
  k_ {y} & -K V^ {2}\\
  0 & k_ {\ theta} -e K V^ {2}
  \ end {array}\ derecha]\). Ahora tienes un conjunto de ecuaciones que, en principio, se pueden resolver para DOF\(y(t)\) y\(\theta(t)\) por transformación de Laplace. Asumir condiciones iniciales nulas\(y(0)=0\) y\(\theta(0)=0\), y asumir que\(F_{G}(t)\) y\(M_{G}(t)\) son funciones transformables de Laplace, luego expresar las ecuaciones de movimiento transformadas por Laplace en la siguiente forma, escribiendo polinomios cuadráticos explícitos (in\(s\)) para los cuatro\(M_{i j}(s ; V)\) elementos de la matriz de coeficientes del lado izquierdo:\ [\ left [\ begin {array} {ll}
  M_ {11} (s; V) & M_ {12} (s; V)\\
  M_ {21} (s; V) & M_ {22} (s; V)
  \ end {array}\ right]\ left [\ begin {array} {l}
  Y (s)\
  \ Theta (s)
  \ end {array}\ derecha]\ equiv [\ mathbf {M} (s; V)]\ left [\ begin {array} {c}
  Y (s)\
  \ theta (s)
  \ end {array}\ right] =\ left [\ begin {array} {c}
  L\ left [F_ {G} (t)\ right]\
  L\ left [M_ {G} (t)\ right] +e L\ left [F_ {G} (t)\ right]
  \ end {array}\ right]\ label {eqn:p16.11.3}\] La solución matriz de Ecuación\(\ref{eqn:eqn:P16.11.3}\) puede escribirse como\ [\ left [\ begin {array} {c}
  Y (s)\
  \ Theta (s)
  \ end {array}\ right] = [\ mathbf {T}\ mathbf {F} (s; V)]\ left [\ begin {array} {c}
  L\ left [F_ {G} (t)\ right]\
  L\ left [M_ {G} (t)\ right] +e L\ left [F_ {G} (t)\ right]
  \ end {array}\ derecha]\ label {eqn:p16.11.4}\] donde la matriz de\(2 \times 2\) coeficientes\([\mathrm{TF}(s ; V)]=[\mathbf{M}(s ; V)]^{-1}\) es la matriz de función de transferencia de múltiples entradas y múltiples salidas (MIMO) que relaciona dos salidas,\(Y(s)\) y\(\Theta(s)\), a dos entradas,\(L\left[F_{G}(t)\right]\) y\(\left(L\left[M_{G}(t)\right]+e L\left[F_{G}(t)\right]\right)\); sin embargo, está claro que cada elemento de la matriz\([\mathbf{T F}(s ; V)]\) es en sí mismo una sola entrada-salida única (SISO) función de transferencia. Utilice las Ecuaciones 12.2.16-12.2.18 para escribir una ecuación para\([\mathbf{T F}(s ; V)]\) en términos de los cuatro\(M_{i j}(s ; V)\) elementos. Obsérvese, en particular, que el denominador de cada una de las funciones de transferencia de SISO\(T F_{i j}(s ; V)\),, es el determinante\(\operatorname{det}[\mathbf{M}(s ; V)]=M_{11}(s ; V) \times M_{22}(s ; V)-M_{21}(s ; V) \times M_{12}(s ; V)\). Por la lógica de la Sección 16.1, por lo tanto, la ecuación quártica (in\(p\)) polinómica\(\operatorname{det}[\mathbf{M}(p ; V)]=0\),, es la ecuación característica general del sistema, y sus cuatro raíces\(p_{i}(V)\) en cada velocidad aérea de transmisión libre\(V\) determinan tanto el carácter de respuesta de tiempo no forzada (e.g. exponencial, oscilatoria, etc.) y la estabilidad o inestabilidad del sistema a esa velocidad aerodinámica particular.
2. En esta parte, utilizará las ecuaciones de la parte 16.11.1 para calcular y trazar los loci de raíces, ya que la velocidad del aire de transmisión libre del túnel de viento\(V\) varía, utilizando parámetros numéricos que fueron seleccionados para representar el proyecto de investigación de un grupo brasileño, DeMarqui, et al., 2005 y 2006. Los parámetros del perfil aerodinámico de sección típica y la atmósfera del túnel de viento son:
  Masa\(m\) = 18.0 kg
  
  Inercia rotacional alrededor del centro de masa\(C\):\(J_C\) = 0.219 kg-m ²; así\(J_{E A}=J_{C}+m r^{2}\)
  
  Desplazamiento del centro de masa\(C\) hacia delante del eje elástico\(EA\):\(r\) = 5 mm = 0.005 m
  
  Constante de rigidez del muelle de traslación vertical:\(k_y\) = 1,110 N/m
  
  Constante de rigidez del muelle de rotación-cabeceo:\(k_\theta\) = 49.8 N-m/radián
  
  Constante de amortiguación de viscosidad del muelle de traslación vertical:\(c_{\theta}=0.00318\) s\(\times k_{y}\)
  
  Constante de amortiguación de la viscosidad del muelle de rotación-cabeceo:\(c_{\theta}=0.00318\) s\(\times k_{\theta}\)
  
  Forma en planta: acorde\(c\) = 0.45 m; span = 0.80 m; así, área\(S=c \times\) span = 0.36 m ²
  
  \(\frac{1}{4}\)Desplazamiento del centro aerodinámico de la cuerda\(AC\) hacia delante del eje elástico\(E A: d=c / 4\)
  
  \(\frac{3}{4}\)Desplazamiento del punto de paso dinámico de cuerda en\(D\) popa del eje elástico\(E A: d=c / 4\)
  
  Densidad estándar del aire a 800 m de altitud promedio de Sao Paulo, Brasil:\(\rho=1.1337\) kg/m ³
  
  Pendiente de la curva de elevación para esta superficie aerodinámica de baja relación de aspecto:\(C_{L \alpha}=2.64\) por radián
  
  El resultado único más significativo que busca es la velocidad del aire de transmisión libre del túnel de viento\(V_F\) a la que la sección típica experimenta aleteo aeroelástico. La velocidad aerodinámica del aleteo\(V_F\) es aquel valor\(V\) en el que la respuesta de tiempo dominante de la sección típica es una sinusoide pura; para velocidades de aire más bajas\(0 \leq V<V_{F}\),, la respuesta dominante es oscilación estable amortiguada positivamente; pero para velocidades de aire más altas,\(V>V_{F}\), la respuesta dominante es inestable que se expande exponencialmente la oscilación. Comience el análisis numérico usando la Ecuación 11.3.10 para calcular la velocidad aeroelástica de divergencia aeroelástica\(V_{D}\) en m/s; porque generalmente\(V_{D}>V_{F}\), este valor de le\(V_{D}\) sugerirá el rango de velocidades aerodinámicas\(0 \leq V<V_{D}\), sobre el cual se deben calcular los loci de raíces con el fin de determinar\(V_{F}\). Utilice las operaciones conv y root de MATLAB para calcular, imprimir y trazar los loci de raíces de la ecuación característica\(M_{11}(p ; V) \times M_{22}(p ; V)-M_{21}(p ; V) \times M_{12}(p ; V)=0\). Puede resultarle útil la forma del script MATLAB M-file MatlabDEMO164.m que produjo las Figuras 16.5.1 y 16.5.5 en la Sección 16.5. En este problema, la velocidad de transmisión libre\(V\) juega el mismo papel que\(\Lambda\) juega el parámetro de ganancia de control en MatlabDemo164.m.

¹ Culick, F.E.C.: “Construyendo un 'Flyer'Wright 1903, por Comité”, Documento 88-0094 de la AIAA, 1988

² Este ejercicio requiere varios cálculos. En lugar de calcular manualmente, es posible que prefiera usar software simbólico. Si usa Symbolic Math Toolbox de MATLAB (ver tarea Problema 1.6), tenga en cuenta que este software simbólico realiza cálculos exactamente, expresando números como fracciones de enteros si es posible. Pero los enteros en estas fracciones pueden llegar a ser bastante grandes y poco manejables. Puede convertir estas fracciones en números decimales usando “v ariable p recisión a ritmético”. Por ejemplo, si un término simbólico se expresa como v = 4115/2263*w, puede convertir el coeficiente fraccionario en un decimal de cinco dígitos con las operaciones >> dígitos (5); v5=vpa (v), cuyo resultado es v5 = 1.8184*w.