17.1: Márgenes de ganancia, márgenes de fase y diagramas de Bode

^{Para describir e ilustrar la forma más básica de análisis de estabilidad de frecuencia-respuesta, consideramos nuevamente un sistema familiar del Capítulo 16: el sistema de control de posición-retroalimentación del rotor con un filtro paso bajo de primer orden en la rama de retroalimentación, para lo cual el diagrama funcional es la Figura 16.3.1} y el diagrama de bloques es la Figura 16.3.2. Ya hemos estudiado este sistema para determinar la estabilidad absoluta según los criterios de Routh en la Sección 16.3, y la estabilidad relativa calculando loci de raíces y aplicando el método root-locus en las Secciones 16.5 y 16.6. Conocer de antemano las características de estabilidad nos guiará en la interpretación del análisis de frecuencia-respuesta.

Figura\(\PageIndex{1}\) (Copyright; autor vía fuente)

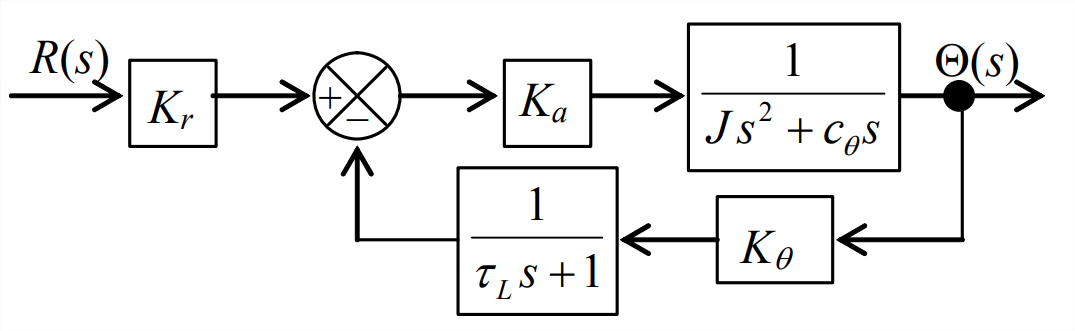
Las funciones de transferencia de ramificación para el bucle en la Figura 16.3.2 son

\[G(s)=\frac{K_{a}}{J s^{2}+c_{\theta} s} \quad \text { and } \quad H(s)=\frac{K_{\theta}}{\tau_{L} s+1}\label{eqn:17.1} \]

La función de transferencia de bucle cerrado es\(C L T F(s)=G(s) /[1+G(s) H(s)]\); el denominador de\(\operatorname{CLTF}(s)\) en esta forma para el sistema de la Figura 16.3.2 es

\[1+G(s) H(s)=1+\frac{K_{a}}{J s^{2}+c_{\theta} s} \times \frac{K_{\theta}}{\tau_{L} s+1}=1+\frac{K_{a} K_{\theta}}{J} \frac{1 / \tau_{L}}{s\left(s+c_{\theta} / J\right)\left(s+1 / \tau_{L}\right)} \equiv 1+\Lambda \frac{\omega_{b}}{s\left(s+c_{\theta} / J\right)\left(s+\omega_{b}\right)} \equiv 1+O \operatorname{LTF}(s)\label{eqn:17.2} \]

donde\(\Lambda \equiv K_{a} K_{\theta} / J\) está el parámetro de control, que ahora llamamos ganancia. Evaluamos la estabilidad del sistema de bucle cerrado en\(\Lambda\) rangos de 0 a\(+\inf\). Las constantes del sistema del Capítulo 16 son\(\omega_{b} \equiv 1 / \tau_{L}=300\) rad/s y\(c_{\theta} / J\) = 100 s ^-1. En la Sección 16.5, resolvimos la ecuación característica del sistema de bucle cerrado,\(1+G(s) H(s)=0\). ¹ Sabemos por los loci de raíces calculados para este sistema que, con ganancia\(\Lambda\) positiva y creciente, existe un valor particular\(\Lambda\) para el cual los loci oscilatorios de raíces se cruzan con el\(\operatorname{Im}[s]\) eje; para este valor de\(\Lambda\), la respuesta oscilatoria de tiempo es puramente sinusoidal y periódica, sin ninguna envolvente exponencial. Definamos esa intersección como el punto de tabilidad oscilatoria n eutral y denotemos el valor de\(\Lambda\) ahí como\(\Lambda_{n s}\) (lo mismo que\(\Lambda_{u b}\) en la Sección 16.5). En consecuencia, denotemos la frecuencia oscilatoria en ese punto como\(\omega_{n s}\) (lo mismo que\(\omega_{d}\) en la Sección 16.5). Determinamos en el Capítulo 16 que\(\Lambda_{n s}=\left(c_{\theta} / J\right) \times \left(c_{\theta} / J+\omega_{b}\right)=40,000\) s ^-2 y\(\omega_{n s}=\sqrt{\left(c_{\theta} / J\right) \omega_{b}}=173.2\) rad/s, y que el sistema de bucle cerrado es exponencialmente estable para\(0<\Lambda<\Lambda_{n s}\), pero inestable para\(\Lambda>\Lambda_{n s}\).

Los loci de raíces se definen por la ecuación característica:

\[1+G(s) H(s) \equiv 1+O \operatorname{LTF}(s)=0\label{eqn:17.3} \]

Por lo tanto, en el punto de estabilidad neutra, con\(\Lambda=\Lambda_{n s}\) y\(s=j \omega_{n s}\), tenemos

\[1+O \operatorname{LTF}\left(j \omega_{n s}\right)=0 \Rightarrow \operatorname{OLTF}\left(j \omega_{n s}\right)=-1=1 \times \exp [j(\pm \pi, \pm 3 \pi, \ldots)] \nonumber \]

\[\operatorname{OLTF}\left(j \omega_{n s}\right) \equiv\left|O \operatorname{LTF}\left(j \omega_{n s}\right)\right| \exp \left[j \angle O \operatorname{LTF}\left(j \omega_{n s}\right)\right]=1 \times \exp [j(\pm \pi, \pm 3 \pi, \ldots)] \nonumber \]

Equiparar proporciones de magnitud y ángulos de fase en la última ecuación da para\(\Lambda=\Lambda_{n s}\):

\[\left|O L T F\left(j \omega_{n s}\right)\right|=1 \quad \text { and } \quad \angle O L T F\left(j \omega_{n s}\right)=(\pm \pi, \pm 3 \pi, \ldots)\label{eqn:17.4} \]

Las ecuaciones\(\ref{eqn:17.4}\) corresponden físicamente, para\(\omega=\omega_{n s}\), a la prueba de frecuencia-respuesta representada en la Figura\(\PageIndex{2}\) (una modificación de la Figura 16.3.1) a continuación. Para la excitación de señal eléctrica sinusoidal de estado estacionario del sistema\(e_{i n}(t)=E_{i n} \sin \omega_{n s} t\) de bucle abierto a la frecuencia de estabilidad neutra del sistema de bucle cerrado,\(\omega=\omega_{n s}\), la relación de magnitud de la respuesta de frecuencia de bucle abierto es exactamente 1 y la señal eléctrica de salida está exactamente desfasada con la entrada señal, significado\(e_{o u t}(t)=-E_{i n} \sin \omega_{n s} t\).

Figura\(\PageIndex{2}\): Diagrama funcional de las pruebas de frecuencia-respuesta de la porción de bucle abierto de las Figuras 16.3.1 y 16.3.2. (Copyright; autor vía fuente)

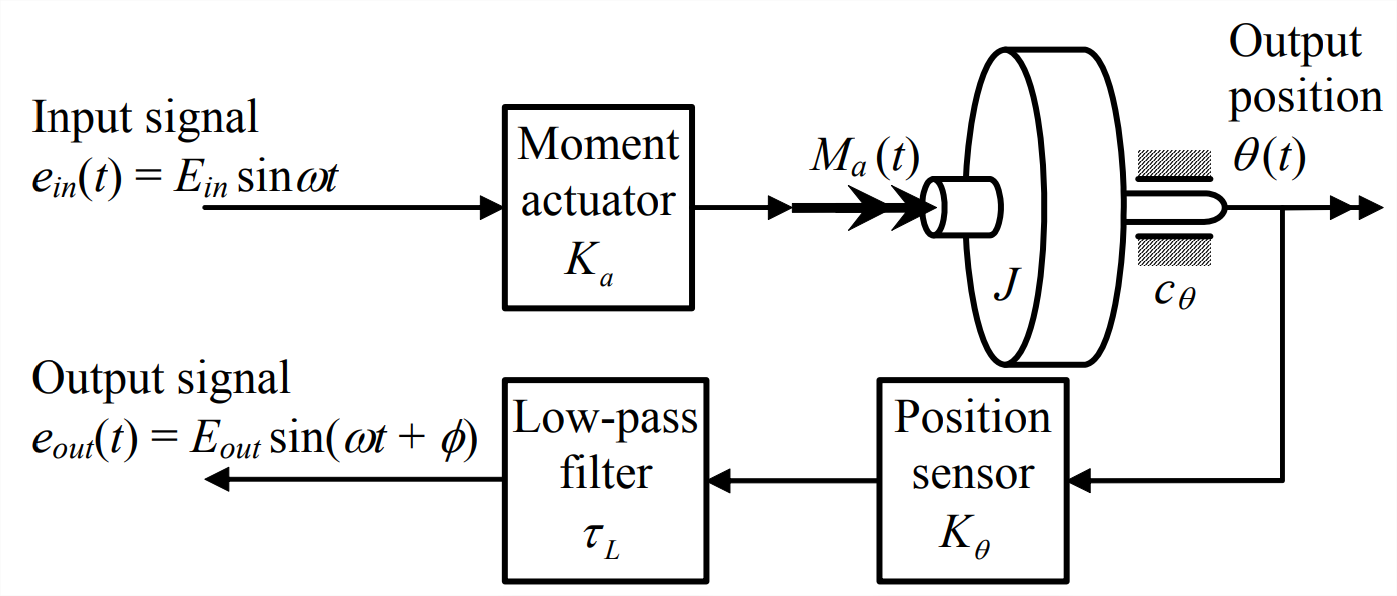
La observación de que, para\(\Lambda=\Lambda_{n s}\), la salida\(e_{\text {out}}(t)=-E_{i n} \sin \omega_{n s} t\) en respuesta a la entrada\(e_{i n}(t)=E_{i n} \sin \omega_{n s} t\) proporciona motivación para realizar pruebas sinusoidales de estado estacionario en el sistema de bucle abierto sobre una banda de frecuencias que rodean\(\omega_{n s}\), no solo\(\omega_{n s}\), y para otros valores de\(\Lambda\), no solo \(\Lambda_{n s}\), con el fin de determinar si este tipo de pruebas proporciona información sobre la estabilidad del sistema de bucle cerrado. Podemos simular tal prueba evaluando numéricamente la función de frecuencia-respuesta de bucle abierto, a partir de la ecuación\(\ref{eqn:17.2}\):

\[O L F R F(\omega) \equiv O L T F(j \omega)=\Lambda \frac{\omega_{b}}{j \omega\left(j \omega+c_{\theta} / J\right)\left(j \omega+\omega_{b}\right)}\label{eqn:17.5} \]

Para comenzar, con el fin de establecer un conjunto de referencia de resultados para el valor de estabilidad neutra de ganancia\(\Lambda=\Lambda_{n s}\), calculamos y trazamos a partir de componentes de\(\ref{eqn:17.5}\) frecuencia-respuesta de Ecuación utilizando el siguiente código MATLAB:

>> wb=300; coj=100; wns=sqrt (wb*coj);

>> wbar=logspace (-1,1,100); w=wbar*wns;

>> lm=4e4; olfrf4e4=lm*wb. /(j*w.* (j*w+coj). * (j*w+wb));

>> subparcela (2,1,1), loglog (wbar, abs (olfrf4e4)), rejilla

>> faz=atan (imag (olfrf4e4). /real (olfrf4e4)) -pi*ones (1, longitud (w));

>> subparcela (2,1,2), semilogx (wbar, faz*180/pi), rejilla

La figura\(\PageIndex{3}\) incluye los resultados gráficos de estas operaciones de MATLAB. Por ahora, nos enfocamos solo en las parcelas de los componentes polares, relación de magnitud y ángulo de fase, para\(\Lambda=\Lambda_{n s}=40,000\) s ^-2; las anotaciones adicionales en la gráfica de fase para “PM” a otros valores de se\(\Lambda\) explicarán a su debido tiempo. Si estuviéramos probando el hardware real de la Figura\(\PageIndex{2}\), en lugar de simplemente simular numéricamente una prueba, entonces la relación de magnitud sería la cantidad\(E_{\text {out}} / E_{\text {in}}\) medida a medida que\(\omega\) se varía la frecuencia, y el ángulo de fase se\(\phi\) calcularía a partir de mediciones por el método presentado en Sección 4.4.

Figura\(\PageIndex{3}\): Diagrama Bode modificado, Ecuación\(\ref{eqn:17.5}\), respuesta de frecuencia para\(\Lambda=\Lambda_{n s}= 40,000\) s ^-2 del sistema de bucle abierto en la Figura\(\PageIndex{2}\) (Copyright; autor vía fuente)

Figura\(\PageIndex{4}\): Relaciones de magnitud, Ecuación\(\ref{eqn:17.5}\) para\(\Lambda = 4,000\) y\(400,000\) s ^-2. (Copyright; autor vía fuente)

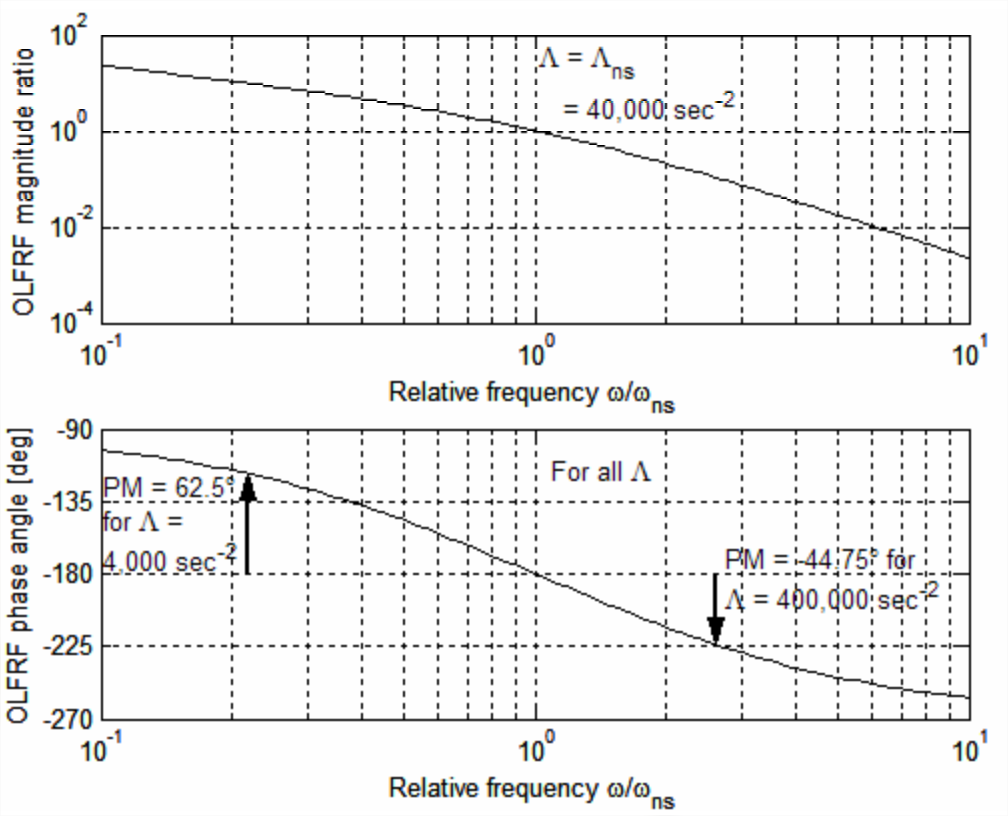
La gráfica superior de la Figura\(\PageIndex{3}\) muestra que, para\(\Lambda=\Lambda_{n s}\), la relación de magnitud\(|O L F R F|\) varía suavemente desde mayor a 10 at\(\omega=0.1 \omega_{n s}\), pasando por el valor previamente determinado de 1 at\(\omega=\omega_{n s}\), hasta menos de 0.01 at\(\omega=10 \omega_{n s}\). La gráfica inferior muestra que el ángulo de fase\(\angle O L F R F\) es un retraso que va desde más de −90° a\(\omega=0.1 \omega_{n s}\), a través de la fase previamente determinada de −180° a\(\omega=\omega_{n s}\), hasta un retraso que se aproxima a −270° a\(\omega=10\omega_{n s}\). Tenemos de Ecuación\(\ref{eqn:17.4}\) para\(\Lambda=\Lambda_{n s}\)\(\angle O L F R F\left(\omega_{n s}\right)=(\pm \pi, \pm 3 \pi, \ldots)\), que es ambigua con respecto al múltiplo y signo de\(\pi\) que es apropiado; la gráfica de fase de Figura\(\PageIndex{3}\) elimina la ambigüedad, al menos para este sistema: claramente,\(\angle O L F R F\left(\omega_{n s}\right)=-\pi\) rad. ²

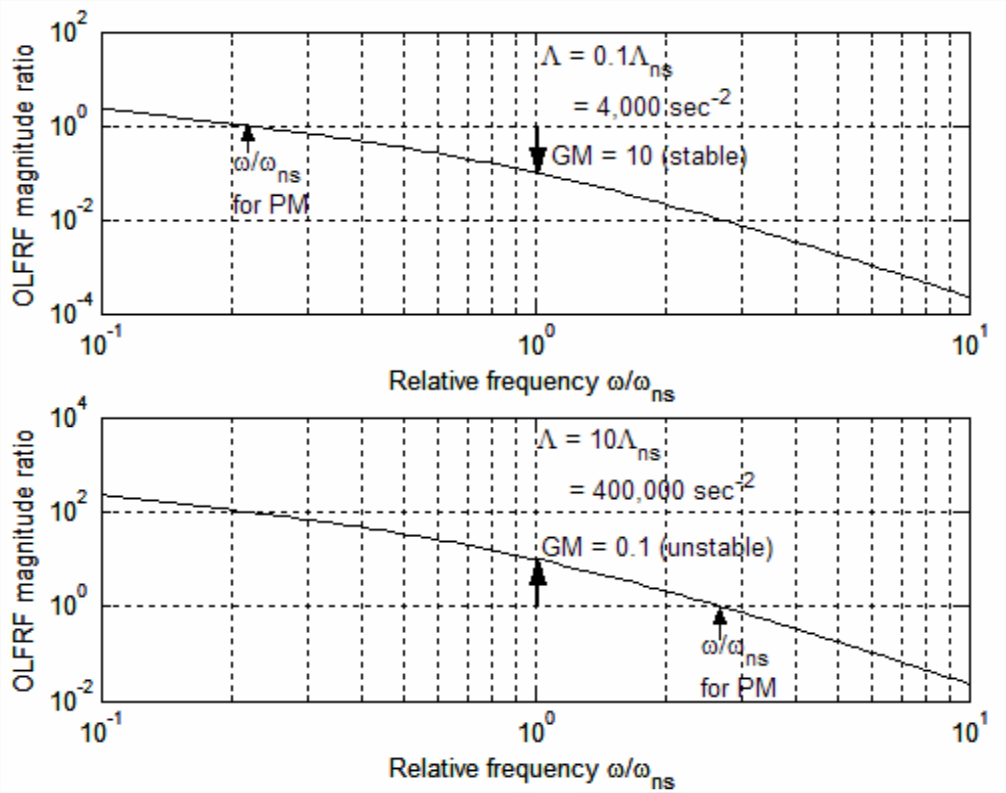
Con la Figura\(\PageIndex{3}\) for\(\Lambda=\Lambda_{n s}\) como la respuesta de frecuencia de bucle abierto de referencia que representa el sistema de bucle cerrado neutralmente estable, ahora podemos calcular respuestas de frecuencia simuladas de bucle abierto para otros valores de\(\Lambda\), específicamente, aquellos para los que el sistema de bucle cerrado es oscilatorio y cualquiera exponencialmente estable o inestable. Con el siguiente código MATLAB, calculamos y trazamos en la Figura\(\PageIndex{4}\) (en la página anterior) los gráficos de relación magnitud-respuesta (solo) para la ganancia\(\Lambda=0.1 \Lambda_{n s}=4,000\) s ^-2, para lo cual sabemos que el sistema de bucle cerrado es estable, y para la ganancia\(\Lambda=10 \Lambda_{n s}=400,000\) s ^-2, para que sabemos que el sistema de bucle cerrado es inestable:

>> wb=300; coj=100; wd=sqrt (wb*coj);

>> wbar=logspace (-1,1,100); w=wbar*wd;

>> lm=4e3; olfrf4e3=lm*wb. /(j*w.* (j*w+coj). * (j*w+wb));

>> lm=4e5; olfrf4e5=lm*wb. /(j*w.* (j*w+coj). * (j*w+wb));

>> subparcela (2,1,1), loglog (wbar, abs (olfrf4e3)), rejilla

>> subparcela (2,1,2), loglog (wbar, abs (olfrf4e5)), rejilla

Si tuviéramos que calcular los ángulos de fase para cualquier valor de\(\Lambda\), encontraríamos que son idénticos a los de la gráfica de ángulo de fase\(\Lambda=\Lambda_{n s}\) de la Figura\(\PageIndex{3}\), que es la razón para no repetir los cálculos de ángulo de fase. (La teoría detrás de esta característica del ángulo de fase de bucle abierto, y también la variación de la magnitud de bucle abierto para diferentes valores de\(\Lambda\), se presentará al final de esta sección.)

Al comparar las gráficas de relación de magnitudes de bucle abierto de Figuras\(\PageIndex{3}\) y\(\PageIndex{4}\), observamos que las magnitudes para el caso\(\Lambda=0.1 \Lambda_{n s}\) estable de bucle cerrado son menores que las de estabilidad neutra\(\Lambda=\Lambda_{n s}\), y las magnitudes para el caso\(\Lambda=10 \Lambda_{n s}\) inestable son mayores. De esto concluimos que las magnitudes de bucle abierto menores o mayores que las de estabilidad neutra son una indicación de estabilidad absoluta en bucle cerrado. Si calculáramos las relaciones de magnitud de bucle abierto para otros valores entre\(0.1 \Lambda_{n s}\) y\(10 \Lambda_{n s}\), encontraríamos que la variación es monótona y regular; esto sugiere que la magnitud de bucle abierto también puede proporcionar una métrica para la estabilidad relativa de bucle cerrado, es decir, la grado de estabilidad o inestabilidad. De hecho, existe una métrica comúnmente aceptada llamada gain margin (\(\text { GM }\)); si denotamos el margen de ganancia para un valor particular de\(\Lambda\) as\(\operatorname{GM}(\Lambda)\), entonces se define como la siguiente relación adimensional de magnitudes de bucle abierto:

\[\operatorname{GM}(\Lambda) \equiv \frac{\left|O L F R F\left(\omega_{n s}\right)\right|_{\Lambda_{n s}} \mid \text { at }\left.\angle O L F R F\left(\omega_{n s}\right)\right|_{\Lambda_{n s}}=-180^{\circ}}{|O L F R F(\omega)|_{\Lambda} \mid \text { at }\left.\angle O L F R F(\omega)\right|_{\Lambda}=-180^{\circ}}=\frac{1}{|O L F R F(\omega)|_{\Lambda} \mid \text { at }\left.\angle O L F R F(\omega)\right|_{\Lambda}=-180^{\circ}}\label{eqn:17.6} \]

En la segunda forma de Ecuación\(\ref{eqn:17.6}\), que es la definición de trabajo, aplicamos el valor de magnitud unitario derivado en Ecuación\(\ref{eqn:17.4}\). La condición\(\left.\angle O L F R F(\omega)\right|_{\Lambda}=-180^{\circ}\) se denomina, descriptivamente, un cruce de fase.

Aplicando Ecuación\(\ref{eqn:17.6}\) a las Figuras\(\PageIndex{3}\) y\(\PageIndex{4}\), calculamos estos márgenes de ganancia:\(\mathrm{GM}\left(0.1 \Lambda_{n s}\right)=10\) para el sistema estable de bucle cerrado; y\(\operatorname{GM}\left(10 \Lambda_{n s}\right)=0.1\) para el sistema inestable. Claramente,\(\mathrm{GM}>1\) implica estabilidad de bucle cerrado e\(0<\mathrm{GM}<1\) implica inestabilidad. Expresar\(\text { GM }\) en términos de su logaritmo a la base 10 (denotado “log”) también es de valor, ya que en esta forma\(\text { GM }\) es positivo para estabilidad de bucle cerrado, cero para estabilidad neutra y negativo para inestabilidad. Es tradicional en la ingeniería de sistemas de control expresar\(\text { GM }\) en decibelios (dB), en cuya unidad el valor de un número positivo\(N\) es\(20 \times \log N\) dB. En consecuencia,\(\operatorname{GM}\left(0.1 \Lambda_{n s}\right)=+20\) dB para el caso estable de bucle cerrado de la Figura\(\PageIndex{4}\), y\(\operatorname{GM}\left(10 \Lambda_{n s}\right)=-20\) dB para el caso inestable.

Otra métrica de frecuencia-respuesta de bucle abierto para el grado de estabilidad de bucle cerrado es el margen de fase (PM). El margen de fase para un valor dado del parámetro\(\Lambda\) de control se define como el ángulo de retardo a la frecuencia para la cual la relación de magnitud es la unidad en relación con el ángulo de retardo comparable para el caso de estabilidad neutra,\(\Lambda=\Lambda_{n s}\):

\[\operatorname{PM}(\Lambda)=\left(\left.\angle O L F R F(\omega)\right|_{\Lambda} \text { at }|O L F R F(\omega)|_{\Lambda} \mid=1\right)-\left(\left.\angle O L F R F\left(\omega_{n s}\right)\right|_{\Lambda_{n s}} \text { at }\left|O L F R F\left(\omega_{n s}\right)\right|_{\Lambda_{n s}} \mid=1\right) \nonumber \]

A partir de la ecuación\(\ref{eqn:17.4}\) y la gráfica de fase de la figura\(\PageIndex{3}\), el ángulo de retardo de referencia es de solo −180°, entonces

\[\operatorname{PM}(\Lambda)=180^{\circ}+\left(\left.\angle O L F R F(\omega)\right|_{\Lambda} \text { at }|O L F R F(\omega)|_{\Lambda} \mid=1\right)\label{eqn:17.7} \]

La condición\(|O L F R F(\omega)|_{\Lambda} \mid=1\) se llama cruce de ganancia. Al leer aproximadamente las fases apropiadas de la gráfica de fases de la Figura\(\PageIndex{3}\), calculamos estos márgenes de fase:\(\operatorname{PM}\left(0.1 \Lambda_{n s}\right) \approx 180^{\circ}-120^{\circ}=+60^{\circ}\) para el sistema estable de bucle cerrado y\(\operatorname{PM}\left(10 \Lambda_{n s}\right) \approx 180^{\circ}-225^{\circ}=-45^{\circ}\) para el sistema inestable. (Ver tarea Problema 17.2 (a) para el cálculo de los valores más precisos de\(\mathrm{PM}\) anotado en la Figura\(\PageIndex{3}\).) Claramente,\(\mathrm{PM}>0^{\circ}\) implica estabilidad de bucle cerrado e\(\mathrm{PM}<0^{\circ}\) implica inestabilidad.

Brogan, 1974, página 25, describió sucintamente la interpretación práctica de estos márgenes de estabilidad para un sistema de bucle cerrado inicialmente estable: “\(\text { GM }\)El margen de ganancia es una medida de ganancia adicional que un sistema puede tolerar sin cambio de fase, mientras permanece estable. El margen de fase\(\mathrm{PM}\) es el desplazamiento de fase adicional que se puede tolerar, sin cambio de ganancia, mientras se mantiene estable”.

Hemos definido e ilustrado márgenes de ganancia y fase para el control de retroalimentación estable e inestable utilizando el sistema físico de las Figuras 16.3.1, 16.3.2 y\(\PageIndex{2}\). El comportamiento de este sistema físico es bastante “común” en el sentido de que es estable para ganancia\(\Lambda=0\) y para valores positivos bajos de\(\Lambda\), pero es inestable para todos los valores\(\Lambda\) mayores que un valor particular de estabilidad neutra,\(\Lambda_{n s}\). Para cualquier sistema físico común, las métricas de frecuencia-respuesta de bucle abierto de margen de ganancia y margen de fase descritas en esta sección son medidas válidas de estabilidad absoluta y relativa. Sin embargo, para sistemas físicos “poco comunes”, los márgenes de ganancia y los márgenes de fase de respuesta de frecuencia de bucle abierto pueden ser ambiguos y difíciles de interpretar; por ejemplo, un sistema tan poco común podría tener\(\mathrm{PM}=+78^{\circ}\) pero\(\mathrm{GM}=-10\) dB, pero aún así ser estable en bucle cerrado. Para sistemas tan poco comunes, un enfoque más general e involucrado, pero inequívoco, del análisis de frecuencia-respuesta se basa en el criterio de estabilidad Nyquist, que es el tema de la Sección 17.3.

Ahora que sabemos calcular las respuestas de frecuencia de bucle abierto en el formato de Figures\(\PageIndex{3}\) y\(\PageIndex{4}\) usando comandos estándar de MATLAB, es apropiado que no tengamos que hacerlo para cada problema, sino que, en su lugar, podamos aplicar las funciones integradas de MATLAB margin and bode para producir más fácilmente los mismos resultados. Antes de llamar a una de estas funciones, primero es necesario definir con el comando tf un modelo de función de transferencia de tiempo lineal (LTI) de MATLAB. A continuación, para la ganancia\(\Lambda=10 \Lambda_{n s}\) del mismo sistema que el de Figuras\(\PageIndex{3}\) y\(\PageIndex{4}\), se muestra una de las muchas formas de hacerlo, junto con las respuestas de MATLAB:

>> wb=300; coj=100;

>> s=tf ('s')

Función de transferencia:

s

>> lm=4e5; oltf4e5=lm*wb/ (s* (s+coj) * (s+wb))

Función de transferencia:

1.2e008

— s^3 + 400 s^2 + 30000 s

>> margen (oltf4e5)

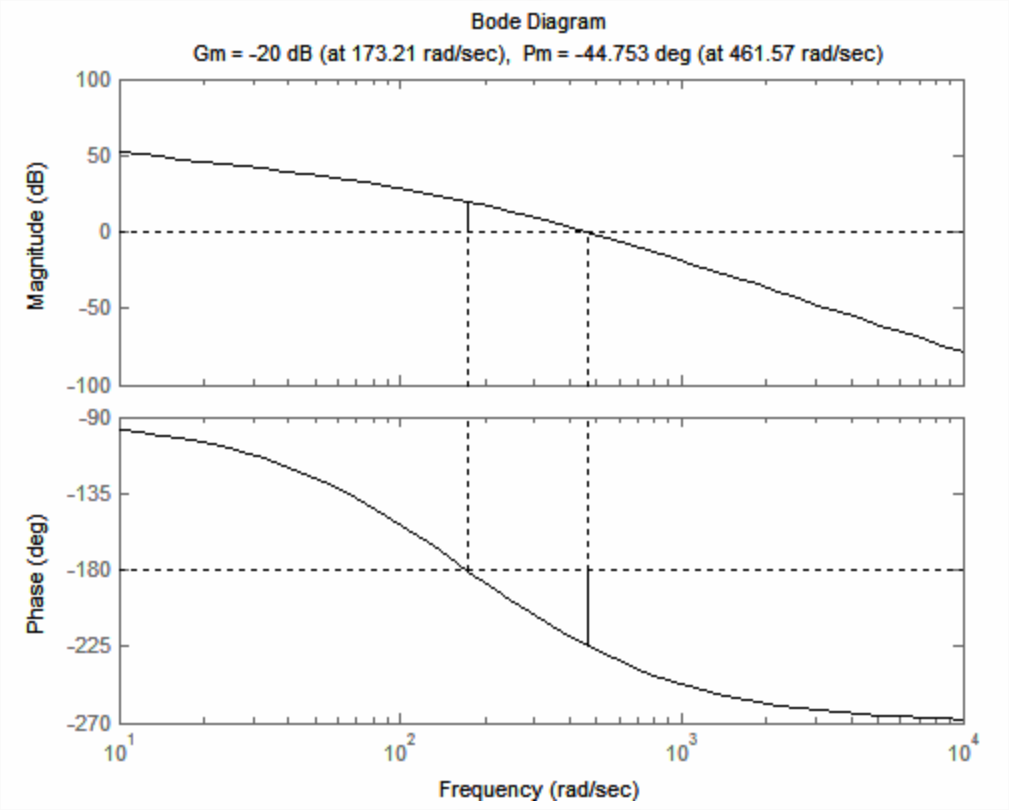
Este comando de margen produjo el diagrama Bode o gráfico de Figura\(\PageIndex{5}\) (página siguiente), que se anota con el\(\mathrm{GM}\) y\(\mathrm{PM}\) para este caso\(\Lambda=10 \Lambda_{n s}\),, el del sistema inestable de bucle cerrado. (La función bode en sí misma también produce el diagrama Bode, pero sin calcular e imprimir el\(\mathrm{GM}\) y\(\mathrm{PM}\).) Obsérvese que no fue necesario especificar la banda de frecuencia—Matlab eligió una banda apropiada. Al comparar Figura\(\PageIndex{5}\) con Figuras\(\PageIndex{3}\) y\(\PageIndex{4}\), se deben observar algunas diferencias de formato, razón por la cual Figura\(\PageIndex{3}\) se etiqueta como un diagrama Bode “modificado”; pero no hay diferencias en el contenido esencial. Un diagrama tradicional de Bode como Figura\(\PageIndex{5}\) traza la relación frecuencia-magnitud respuesta (en decibelios) versus frecuencia (en rad/s o Hz), que se presenta en una escala logarítmica para acomodar una banda muy ancha.

Figura\(\PageIndex{5}\): Diagrama Bode tradicional de MATLAB, Ecuación\(\ref{eqn:17.5}\), respuesta de frecuencia para\(\Lambda=10 \Lambda_{n s}=400,000\) s ^-2 del sistema de bucle abierto en la Figura\(\PageIndex{2}\). (Copyright; autor vía fuente)

Para concluir esta sección, consideramos para los sistemas en general cómo los cambios en la ganancia\(\Lambda\) influyen en las respuestas de frecuencia de bucle abierto y sus representaciones gráficas en diagramas Bode (y diagramas Nyquist en la Sección 17.4). Se deduce de las ecuaciones 16.6.2 y 16.6.3 que una función de transferencia de bucle abierto generalmente se puede expresar en la forma

\[\operatorname{OLTF}(s)=\Lambda \times T F_{1}(s)\label{eqn:17.8} \]

donde la función\(T F_{1}(s)\) de transferencia de línea base se define obviamente como\(\left.O L T F(s)\right|_{\Lambda=1}\). La función de frecuencia-respuesta general asociada es

\[O L F R F(\omega)=\Lambda \times T F_{1}(j \omega)=\Lambda \times\left|T F_{1}(j \omega)\right| \times \exp \left[j \angle T F_{1}(j \omega)\right]\label{eqn:17.9} \]

La ecuación\(\ref{eqn:17.9}\) conduce a las siguientes formas generales para la relación de magnitud de frecuencia-respuesta de bucle abierto (\(\mathrm{MR}\)) y el ángulo de fase\(\phi\):

\[M R(\omega)=|O L F R F(\omega)|=\Lambda \times\left|T F_{1}(j \omega)\right| \equiv \Lambda \times M R_{1}(\omega)\label{eqn:17.10} \]

\[\phi(\omega)=\angle T F_{1}(j \omega)\label{eqn:17.11} \]

\(\ref{eqn:17.11}\)La ecuación muestra que la variación del ángulo de fase con la frecuencia\(\phi(\omega)\),, es la misma para todos los valores de ganancia\(\Lambda\), como se indicó anteriormente en el contexto de las Figuras\(\PageIndex{3}\) y\(\PageIndex{4}\).

En la forma final de Ecuación\(\ref{eqn:17.10}\), definimos la relación de magnitud basal (es decir, para ganancia de unidad,\(\Lambda=1\)) como\(M R_{1}(\omega) \equiv\left|T F_{1}(j \omega)\right|\). También es informativo expresar Ecuación\(\ref{eqn:17.10}\) en forma logarítmica, ya sea en logaritmo a base 10 como en Figuras\(\PageIndex{3}\) y\(\PageIndex{4}\), o en decibelios como en una gráfica tradicional de Bode como la Figura\(\PageIndex{5}\):

\[\log (M R(\omega))=\log (\Lambda)+\log \left(M R_{1}(\omega)\right)\label{eqn:17.12a} \]

\[20 \times \log (M R(\omega)) \equiv[M R(\omega)](\mathrm{dB})=[\Lambda](\mathrm{dB})+\left[M R_{1}(\omega)\right](\mathrm{dB})\label{eqn:17.12b} \]

Inferimos de Ecuaciones\(\ref{eqn:17.10}\),\(\ref{eqn:17.12a}\), y\(\ref{eqn:17.12b}\) que la forma gráfica de la variación funcional con relación de frecuencia de magnitud\(M R(\omega)\) no cambia con los cambios en la ganancia\(\Lambda\). Para gráficas Bode modificadas como Figuras\(\PageIndex{3}\) y\(\PageIndex{4}\), dada la curva de línea base\(M R_{1}(\omega)\), podemos encontrar en Ecuación\(\ref{eqn:17.12a}\) la curva para cualquier otra ganancia\(\Lambda>1\) simplemente agregando a la curva de línea base el valor\(\log (\Lambda)\), que mueve toda la curva hacia arriba por la distancia\(\log (\Lambda)\) a lo largo del eje de relación de magnitud. El proceso de búsqueda de curvas para diferentes ganancias\(\Lambda\) a partir de Ecuación\(\ref{eqn:17.12b}\) es fácil para una gráfica tradicional de Bode como Figura\(\PageIndex{5}\), en la que la magnitud se grafica en decibelios con una escala lineal. Por ejemplo, podemos encontrar a partir de\(\PageIndex{5}\) la Figura la curva de magnitud para\(\Lambda=40,000\) s ^-2 simplemente moviéndose hacia abajo en 20 dB, es decir, por\(20 \times [\log (40,000)-\log (400,000)]\), la curva de magnitud para\(\Lambda=400,000\) s ^-2.

¹ Utilizamos la variable compleja de Laplace\(s\) en este capítulo porque es tradicional para el tratamiento de la teoría de frecuencia-respuesta usar\(s\), en lugar de una variable compleja\(p\) (para\(s = p\), una solución de la ecuación característica, es decir, un polo de la función de transferencia de bucle cerrado) que usamos en las Secciones 16.3 a 16.6.

² La línea de código MATLAB que calcula la fase requiere que los ángulos estén entre\(-\pi / 2\) y\(-3\pi / 2\) rad, por lo que el argumento aquí parece ser circular. Sin embargo, si tuviéramos que usar el ángulo de función MATLAB más general en lugar de esa línea de código, encontraríamos, en el rango de\(0.1 \leq \omega / \omega_{n s}<1.0\), exactamente las mismas fases rezagadas que están en la gráfica de fases de la Figura\(\PageIndex{3}\), lo que valida la afirmación de que el valor apropiado es\(-\pi\) rad . No usamos ángulo, porque aparentemente se basa en la función tangente inversa de cuatro cuadrantes de MATLAB atan2, que devuelve valores de ángulo solo entre\(-\pi\) y\(+\pi\) rad. Por lo tanto, en la gráfica de fase versus\(\omega / \omega_{n s}\), ángulo produciría un salto discontinuo artificial y confuso en fase de −180° a +180°\(\omega / \omega_{n s}=1.0\) y, en el rango de\(1.0 \leq \omega / \omega_{n s} \leq 10\), la fase caería de +180° a un poco más de +90°.