17.4: El Criterio de Estabilidad Nyquist

La Sección 17.1 describe cómo se definen y muestran los márgenes de estabilidad de ganancia (GM) y fase (PM) en las gráficas de Bode. Es informativo y resultará aún más general extraer los mismos márgenes de estabilidad de las parcelas Nyquist de respuesta de frecuencia. Para iniciar este estudio, repetiremos la gráfica Nyquist de la Figura 17.2.2, el caso de estabilidad neutra de bucle cerrado, para el cual\(\Lambda=\Lambda_{n s}=40,000\) s ^-2 y\(\omega_{n s}=100 \sqrt{3}\) rad/s, pero sobre una banda más estrecha de frecuencias de excitación,\(100 \leq \omega \leq 1,000\) rad/s, o\(1 / \sqrt{3} \leq \omega / \omega_{n s} \leq 10 / \sqrt{3}\); la intención aquí es restringir nuestra atención principalmente a la respuesta de frecuencia para la cual el retardo de fase excede aproximadamente 150°, es decir, para lo cual la curva de frecuencia-respuesta en el\(OLFRF\) plano es algo cercana al eje real negativo. Además, agregaremos a la misma gráfica las gráficas Nyquist de respuesta de frecuencia para un caso de estabilidad positiva en bucle cerrado con\(\Lambda=1 / 2 \Lambda_{n s}=20,000\) s ^-2, y para un caso de inestabilidad de bucle cerrado con\(\Lambda= 2 \Lambda_{n s}=80,000\) s ^-2. Los comandos MATLAB siguen que calculan [a partir de las ecuaciones 17.1.7 y 17.1.12] y trazan estos casos de función de frecuencia-respuesta de bucle abierto, y el diagrama Nyquist resultante (después de la edición adicional):

>> wb=300; coj=100; w=logspace (2,3,200);

>> olfrf01=wb. /(j*w.* (j*w+coj). * (j*w+wb));

>> olfrf20k=20e3*olfrf01; olfrf40k=40e3*olfrf01; olfrf80k=80e3*olfrf01;

>> parcela (real (olfrf80k), imag (olfrf80k), real (olfrf40k), imag (olfrf40k),...

real (olfrf20k), imag (olfrf20k)), rejilla

Figura\(\PageIndex{1}\): Gráficas nyquist de la Ecuación 17.1.7, funciones de frecuencia-respuesta de bucle abierto (\(OLFRF\))\(\Lambda=(1 / 2,1, \text { and } 2) \times \Lambda_{n s}\) para el sistema de la Figura 17.1.2, con parámetros\(\omega_b = 300\)\(c_{\theta} / J=100\) s ^{-1, s -1} y\(\omega_{n s}=\sqrt{ \omega_{b} \times c_{\theta} / J}=173.2\) rad/s. (Copyright; author vía fuente)

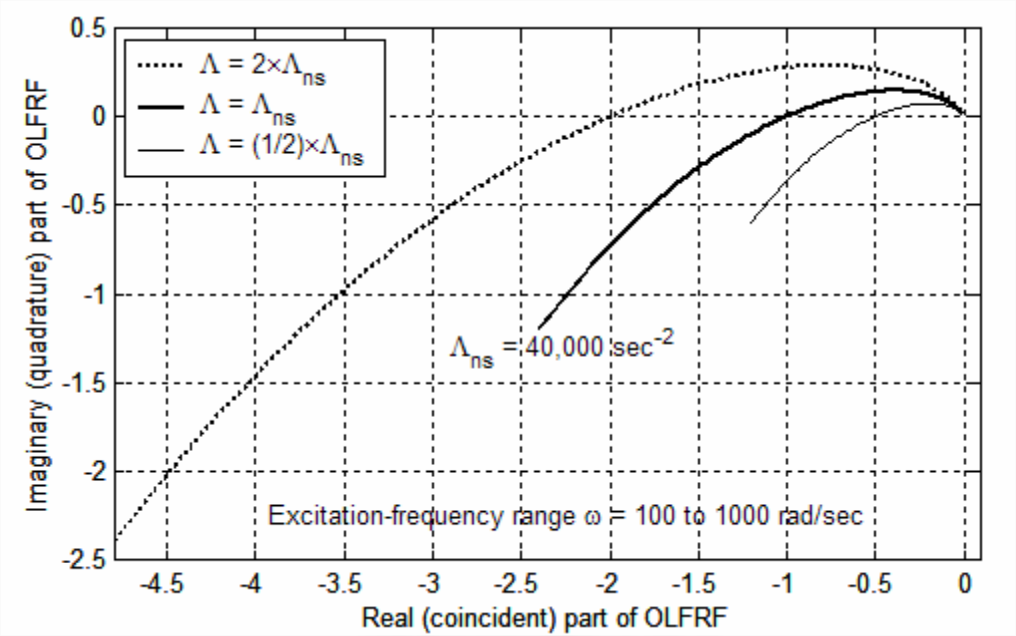
El margen de ganancia y el margen de fase están presentes y son medibles en gráficas Nyquist como las de la Figura\(\PageIndex{1}\). El margen de ganancia (GM) se define por la Ecuación 17.1.8, de la cual encontramos

\[\frac{1}{G M(\Lambda)}=|O L F R F(\omega)|_{\mid} \mid \text {at }\left.\angle O L F R F(\omega)\right|_{\Lambda}=-180^{\circ}\label{eqn:17.17} \]

La ecuación\(\ref{eqn:17.17}\) se ilustra en la Figura tanto\(\PageIndex{2}\) para casos estables como inestables de bucle cerrado. Tenga en cuenta que un caso estable de bucle cerrado tiene\(0<1 / \mathrm{GM}_{\mathrm{S}}<1\) así que\(\mathrm{GM}_{\mathrm{S}}>1\), y un caso inestable de bucle cerrado tiene\(1 / \mathrm{GM}_{\mathrm{U}}>1\) así que\(0<\mathrm{GM}_{\mathrm{U}}<1\).

Figura\(\PageIndex{2}\): Gráficas esquemáticas de Nyquist de funciones de frecuencia-respuesta de bucle abierto (\(OLFRF\)) para casos estables y —inestables en bucle cerrado. (Copyright; autor vía fuente)

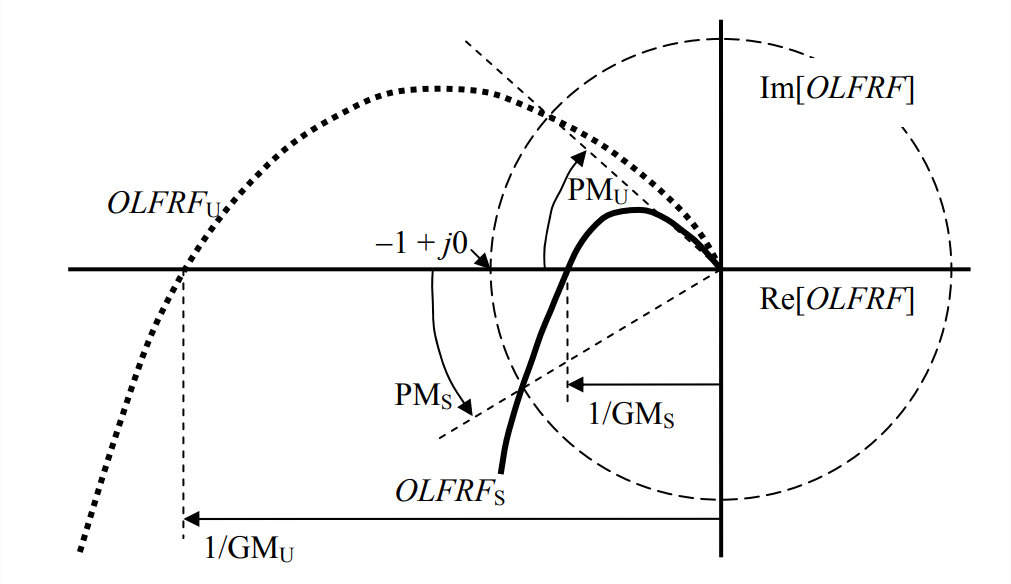
Podemos medir el margen de fase directamente dibujando en el diagrama Nyquist un círculo con radio de 1 unidad y centrado en el origen del\(OLFRF\) plano complejo, para que pase por el punto importante\(-1+j 0\). El margen de fase está definido por

\[\operatorname{PM}(\Lambda)=180^{\circ}+\left(\left.\angle O L F R F(\omega)\right|_{\Lambda} \text { at }|O L F R F(\omega)|_{\Lambda} \mid=1\right)\label{eqn:17.7} \]

Los márgenes de fase se indican gráficamente en la Figura\(\PageIndex{2}\). El positivo\(\mathrm{PM}_{\mathrm{S}}\) para un caso estable en bucle cerrado es el ángulo en sentido contrario a las agujas del reloj desde el\(\operatorname{Re}[O L F R F]\) eje negativo hasta la intersección del círculo unitario con la\(OLFRF_S\) curva; a la inversa, lo negativo\(\mathrm{PM}_U\) para un caso inestable en bucle cerrado es el ángulo en el sentido de las agujas del reloj desde el\(\operatorname{Re}[O L F R F]\) eje negativo a la intersección del círculo unitario con la\(OLFRF_U\) curva.

Observe en la Figura\(\PageIndex{2}\) que el punto de cruce de fase (ángulo de fase\(\phi=-180^{\circ}\)) y el punto de cruce de ganancia (relación de magnitud\(MR = 1\)) de un\(FRF\) son claramente evidentes en una gráfica de Nyquist, quizás incluso más natural que en un diagrama de Bode. Por otro lado, un diagrama de Bode muestra las frecuencias de cruce de fase y de cruce de ganancia, las cuales no son explícitas en una gráfica Nyquist tradicional.

Con un poco de imaginación, inferimos de las gráficas Nyquist de Figura\(\PageIndex{1}\) que el sistema de bucle abierto representado en esa figura tiene\(\mathrm{GM}>0\) y\(\mathrm{PM}>0\) para\(0<\Lambda<\Lambda_{\mathrm{ns}}\), y eso\(\mathrm{GM}>0\) y\(\mathrm{PM}>0\) para todos los valores de ganancia\(\Lambda\) mayores que\(\Lambda_{\mathrm{ns}}\); en consecuencia, los asociados sistema de bucle cerrado es estable para\(0<\Lambda<\Lambda_{\mathrm{ns}}\), e inestable para todos los valores de ganancia\(\Lambda\) mayores que\(\Lambda_{\mathrm{ns}}\). Así, este sistema físico (de las Figuras 16.3.1, 16.3.2 y 17.1.2) se considera un sistema “común”, para el cual el margen de ganancia y el margen de fase proporcionan métricas claras e inequívocas de estabilidad. Consideremos a continuación un sistema “poco común”, para el cual la determinación de estabilidad o inestabilidad requiere un examen más detallado de los márgenes de estabilidad. Supongamos que la función de transferencia de bucle abierto de un sistema es ¹

\[G(s) \times H(s) \equiv O L T F(s)=\Lambda \frac{s^{2}+4 s+104}{(s+1)\left(s^{2}+2 s+26\right)}=\Lambda \frac{s^{2}+4 s+104}{s^{3}+3 s^{2}+28 s+26}\label{eqn:17.18} \]

Debería poder demostrar que los ceros de esta función de transferencia en el\(s\) plano complejo están en (\(−2 ± j10\)), y los polos están en (\(−1 + j0\)) y (\(−1 ± j5\)).

Para establecer la referencia de estabilidad e inestabilidad del sistema de bucle cerrado correspondiente a la Ecuación\(\ref{eqn:17.18}\), determinamos los loci de raíces a partir de la ecuación característica\(1+G H=0\), o

\[s^{3}+3 s^{2}+28 s+26+\Lambda\left(s^{2}+4 s+104\right)=s^{3}+(3+\Lambda) s^{2}+4(7+\Lambda) s+26(1+4 \Lambda)=0\label{17.19} \]

Los siguientes comandos de MATLAB, adaptados del código que produjo la Figura 16.5.1, calculan y trazan los loci de raíces:

Lm= [0 .2 .4 .7 1 1.5 2.5 3.7 4.75 6.5 9 12.5 15 18.5 25 35 50 70 125 250];

NP = longitud (Lm);

para I=1:NP;

A2=3+lm (i); a3 = 4* (7+Lm (i)); a4=26* (1+4*Lm (i));

p (i, 1:3) =raíces ([1 a2 a3 a4]). ' ;

final

plot (p, 'kx'), grid, xlabel ('Parte real del polo (seg^-^1) ')

ylabel ('Parte imaginaria del polo (sec^-^1) ')

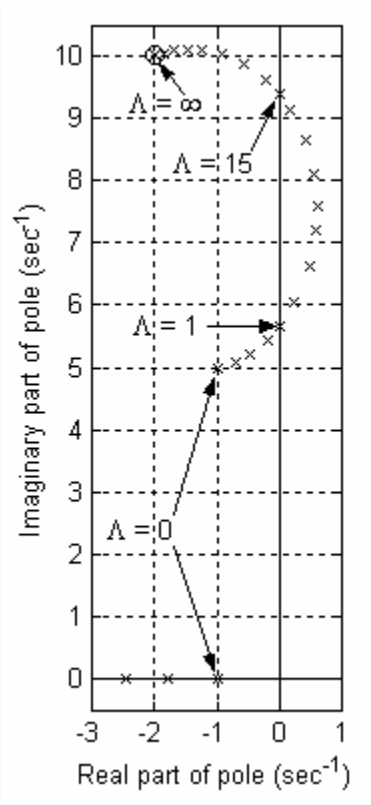
Las raíces significativas de la Ecuación se\(\ref{eqn:17.19}\) muestran en la Figura\(\PageIndex{3}\): se muestra el locus completo de raíces oscilatorias con partes imaginarias positivas; solo se muestra el inicio del locus de raíces reales (exponencialmente estables), ya que esas raíces se vuelven progresivamente más negativas a medida que la ganancia\(\Lambda\) aumenta a partir de los valores pequeños iniciales. Las raíces oscilatorias de la Figura\(\PageIndex{3}\) muestran que el sistema de bucle cerrado es estable\(\Lambda=0\) hasta\(\Lambda \approx 1\), es inestable por\(\Lambda \approx 1\) hasta\(\Lambda \approx 15\), y se vuelve estable nuevamente por\(\Lambda\) más de\(\approx 15\). Consideramos este sistema de bucle cerrado como “poco común” o inusual porque es estable para valores pequeños y grandes de ganancia\(\Lambda\), pero inestable para un rango de valores intermedios.

Si tuviéramos que probar experimentalmente la parte de bucle abierto de este sistema para determinar la estabilidad del sistema de bucle cerrado, ¿cuáles serían las respuestas de frecuencia de bucle abierto para diferentes valores de ganancia\(\Lambda\)? Para simular esa prueba, tenemos de Ecuación\(\ref{eqn:17.18}\), la siguiente ecuación para la función frecuencia-respuesta:

\[O L F R F(\omega) \equiv O L T F(j \omega)=\Lambda \frac{104-\omega^{2}+4 \times j \omega}{(1+j \omega)\left(26-\omega^{2}+2 \times j \omega\right)}\label{eqn:17.20} \]

Comencemos este estudio computándolo\(\operatorname{OLFRF}(\omega)\) y mostrándolo en gráficas Nyquist para un bajo valor de ganancia,\(\Lambda=0.7\) (para lo cual el sistema de bucle cerrado es estable), y para el valor correspondiente a la transición de estabilidad a inestabilidad en Figura\(\PageIndex{3}\), que denotamos como\(\Lambda_{n s 1} \approx 1\). El valor de no\(\Lambda_{n s 1}\) es exactamente 1, como\(\PageIndex{3}\) podría sugerir la Figura; ver tarea Problema 17.2 (b) para el cálculo del valor más preciso\(\Lambda_{n s 1}=0.96438\). Los siguientes comandos de MATLAB calculan y trazan las dos respuestas de frecuencia y también, para determinar los márgenes de fase como se muestra en la Figura\(\PageIndex{2}\), un arco del círculo unitario centrado en el origen del\(O L F R F(\omega)\) plano complejo.

Figura\(\PageIndex{3}\): Loci de raíces de Ecuación\(\ref{eqn:17.19}\). (Copyright; autor vía fuente)

>> w=3.4*logspace (0,2,500);

>> olfrf01 =( 104-w.^2+4*j*w) ./ ((1+j*w) .* (26- w.^2+2*j*w));

>> olfrf007=0.7*olfrf01;

>> parcela (real (olfrf007), imag (olfrf007)), rejilla

>> cirangrad=0.8*pi:0. 01:1 .2*pi;

>> bodega, parcela (cos (cirangrad), pecado (cirangrad))

Parcela actual mantenida

>> olfrfns1=0.96438*olfrf01;

>> parcela (real (olfrfns1), imag (olfrfns1))

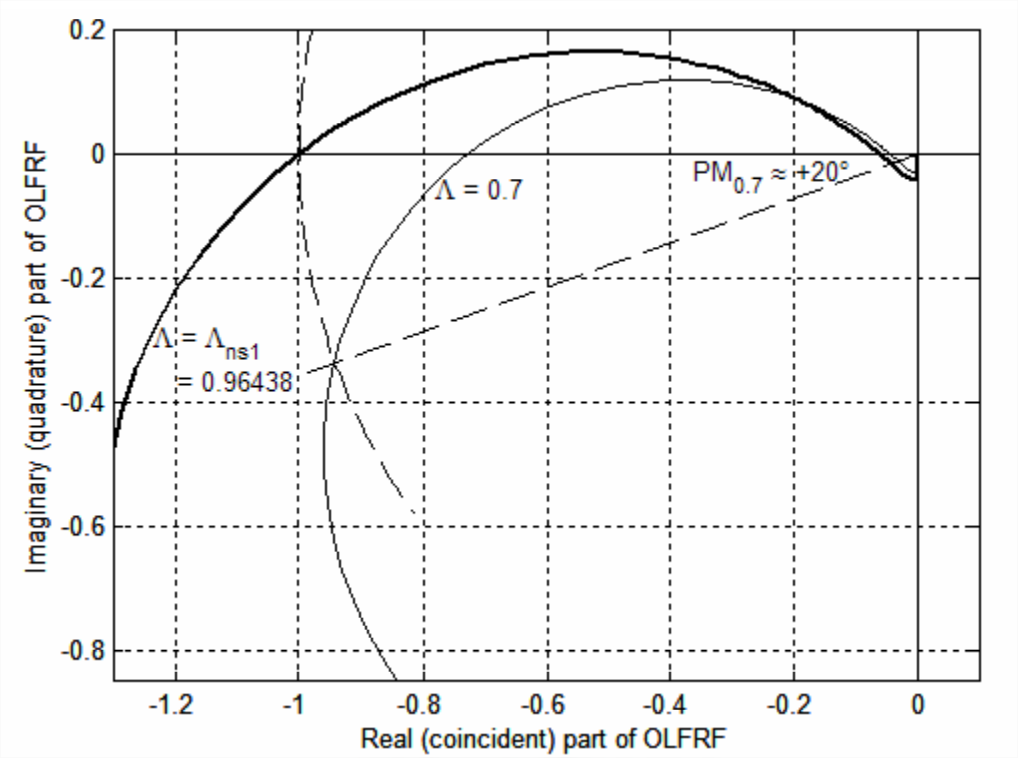
Las porciones de ambas gráficas de Nyquist (para\(\Lambda=0.7\) y\(\Lambda=\Lambda_{n s 1}\)) que están más cerca del\(\operatorname{Re}[O L F R F]\) eje negativo se muestran en la Figura\(\PageIndex{4}\) (página siguiente). Observe en\(\PageIndex{4}\) la Figura los pequeños bucles debajo del\(\operatorname{Re}[O L F R F]\) eje negativo a medida que la frecuencia de conducción se vuelve muy alta: las respuestas de frecuencia se acercan a cero desde debajo del origen del\(OLFRF\) plano complejo. Esto es claramente diferente de las gráficas Nyquist de un sistema de bucle abierto más “común” en la Figura\(\PageIndex{1}\), que se acercan al origen desde arriba a medida que la frecuencia se vuelve muy alta. Otro aspecto de la diferencia entre las gráficas de las dos figuras es particularmente significativo: mientras que las gráficas de la Figura\(\PageIndex{1}\) cruzan el\(\operatorname{Re}[O L F R F]\) eje negativo solo una vez a medida que\(\omega\) aumenta la frecuencia de conducción, las de la Figura\(\PageIndex{4}\) tienen cruces de dos fases, es decir, el ángulo de fase es −180° para dos valores diferentes de\(\omega\). Ya que en la Figura\(\PageIndex{4}\) hay dos frecuencias diferentes en las que\(\left.\angle O L F R F(\omega)\right|_{\Lambda}=-180^{\circ}\), la definición de margen de ganancia en las Ecuaciones 17.1.8 y\(\ref{eqn:17.17}\) es ambigua: ¿a cuál, si alguna, de los cruces de fase es apropiado leer la cantidad\(1 / \mathrm{GM}\), como se muestra en\(\PageIndex{2}\)? ¿Cuál, si alguno de los valores calculados a partir de esa lectura,\(\mathrm{GM}=(1 / \mathrm{GM})^{-1}\) es una métrica legítima de estabilidad de bucle cerrado? \(\PageIndex{4}\)incluye las parcelas Nyquist para ambos\(\Lambda=0.7\) y\(\Lambda =\Lambda_{n s 1}\), este último de los cuales por definición cruza el\(\operatorname{Re}[O L F R F]\) eje negativo en el punto\(-1+j 0\), no muy lejos a la izquierda de donde la\(\Lambda=0.7\) parcela cruza aproximadamente\(-0.73+j 0\); por lo tanto, podría ser que el valor apropiado de margen de ganancia para\(\Lambda=0.7\) se encuentra de\(1 / \mathrm{GM}_{0.7} \approx 0.73\), de modo que\(\mathrm{GM}_{0.7} \approx 1.37=2.7\) dB, un pequeño margen de ganancia que indica que el sistema de bucle cerrado es apenas débilmente estable. Si, por otro lado, tuviéramos que calcular el margen de ganancia usando el otro cruce de fase\(-0.04+j 0\), aproximadamente, entonces eso llevaría al\(\mathrm{GM} \approx 25=28\) dB exagerado, que obviamente es una métrica defectuosa de estabilidad. Tenga en cuenta que el margen de fase para\(\Lambda=0.7\), encontrado como se muestra en la Figura\(\PageIndex{2}\), es bastante claro en Figura\(\PageIndex{4}\) y no en absoluto ambiguo como el margen de ganancia:\(\mathrm{PM}_{0.7} \approx+20^{\circ}\); este valor también indica un sistema estable, pero débilmente así, de bucle cerrado.

Figura\(\PageIndex{4}\): Gráficas Nyquist, Ecuación\(\ref{eqn:17.20}\), funciones de frecuencia-respuesta de bucle abierto (\(OLFRF\)) para\(\Lambda=0.7\) y\(\Lambda=\Lambda_{n s 1}=0.96438\) en el sistema de Ecuación\(\ref{eqn:17.18}\). (Copyright; autor vía fuente)

Continuemos con este estudio computándolo\(OLFRF(\omega)\) y mostrándolo como una gráfica Nyquist para un valor intermedio de ganancia\(\Lambda=4.75\), para lo cual la Figura\(\PageIndex{3}\) muestra que el sistema de bucle cerrado es inestable. Los siguientes comandos de MATLAB calculan [a partir de las ecuaciones 17.1.12 y\(\ref{eqn:17.20}\)] y trazan la respuesta de frecuencia y un arco del círculo unitario centrado en el origen del\(OLFRF(\omega)\) plano complejo.

w=3.4*logspace (0,2,500);

olfrf01 =( 104-w.^2+4*j*w) ./ ((1+j*w) .* (26-w.^2+2*j*w));

>> olfrf0475=4.75*olfrf01;

>> parcela (real (olfrf0475), imag (olfrf0475)), rejilla

>> cirangrad=0.8*pi:0. 01:1 .2*pi;

>> bodega, parcela (cos (cirangrad), pecado (cirangrad))

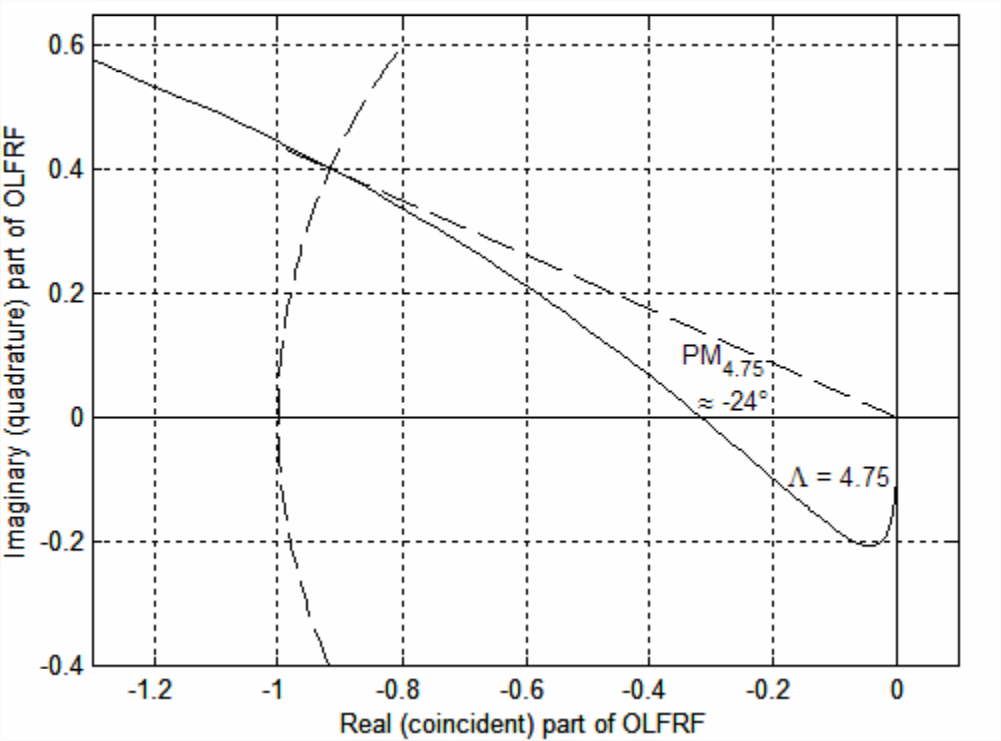
La porción de la gráfica Nyquist para ganancia\(\Lambda=4.75\) que está más cerca del\(\operatorname{Re}[O L F R F]\) eje negativo se muestra en la Figura\(\PageIndex{5}\). La\(\Lambda=\Lambda_{n s 1}\) gráfica de la Figura\(\PageIndex{4}\) se expande radialmente hacia afuera en la Figura\(\PageIndex{5}\) por el factor de\(4.75 / 0.96438=4.9254\), por lo que el bucle para altas frecuencias debajo del\(\operatorname{Re}[O L F R F]\) eje negativo es más prominente que en la Figura\(\PageIndex{4}\). La curva de frecuencia-respuesta que conduce a ese bucle cruza el\(\operatorname{Re}[O L F R F]\) eje aproximadamente\(-0.315+j 0\); si usáramos este cruce de fase para calcular el margen de ganancia, entonces encontraríamos\(\mathrm{GM} \approx 1 / 0.315=3.175=10.0\) dB. Además, si aplicamos para este sistema con\(\Lambda=4.75\) el comando MATLAB margin para generar un diagrama Bode en la misma forma que la Figura 17.1.5, entonces MATLAB anota ese diagrama con los valores\(\mathrm{GM}=10.007\) dB y\(\mathrm{PM}=-23.721^{\circ}\) (lo mismo que PM4.75 que se muestra aproximadamente en la Figura\(\PageIndex{5}\)). Sabemos por Figura\(\PageIndex{3}\) que este caso de\(\Lambda=4.75\) es inestable de bucle cerrado. Sin embargo, el margen de ganancia positivo 10 dB sugiere estabilidad positiva. El margen de fase negativo indica, por el contrario, inestabilidad. Claramente, el cálculo\(\mathrm{GM} \approx 1 / 0.315\) es una métrica defectuosa de estabilidad. El otro cruce de fase, a\(-4.9254+j 0\) (más allá del rango de la Figura\(\PageIndex{5}\)), podría ser el punto apropiado para el cálculo del margen de ganancia, ya que al menos indica inestabilidad,\(\mathrm{GM}_{4.75}=1 / 4.9254=0.20303=-13.85\) dB.

Figura\(\PageIndex{5}\): Gráfica Nyquist, Ecuación\(\ref{eqn:17.20}\), función de frecuencia-respuesta de bucle abierto (\(OLFRF\)) para (\ Lambda=4.75\) en el sistema de Ecuación\(\ref{eqn:17.18}\). (Copyright; autor vía fuente)

Completemos este estudio computándolo\(\operatorname{OLFRF}(\omega)\) y mostrándolo en gráficas Nyquist para el valor correspondiente a la transición de la inestabilidad a la estabilidad en la Figura\(\PageIndex{3}\), que denotamos como\(\Lambda_{n s 2} \approx 15\), y para un valor ligeramente mayor,\(\Lambda=18.5\), para lo cual el sistema de bucle cerrado es estable. El valor de no\(\Lambda_{n s 2}\) es exactamente 15, como\(\PageIndex{3}\) podría sugerir la Figura; ver tarea Problema 17.2 (b) para el cálculo del valor más preciso\(\Lambda_{n s 2} = 15.0356\). Las porciones de ambas gráficas Nyquist (for\(\Lambda_{n s 2}\) y\(\Lambda=18.5\)) que están más cerca del\(\operatorname{Re}[O L F R F]\) eje negativo se muestran en la Figura\(\PageIndex{6}\), la cual fue producida por los comandos de MATLAB que produjeron Figura\(\PageIndex{4}\), excepto con ganancias 18.5 y\(\Lambda_{n s 2}\) reemplazando, respectivamente, ganancias 0.7 y \(\Lambda_{n s 1}\).

Figura\(\PageIndex{6}\): Gráficas Nyquist, Ecuación\(\ref{eqn:17.20}\), funciones de frecuencia-respuesta de bucle abierto (\(OLFRF\)) para\(\Lambda=\Lambda_{n s 2}=15.0356\) y\(\Lambda=18.5\) en el sistema de Ecuación\(\ref{eqn:17.18}\). (Copyright; autor vía fuente)

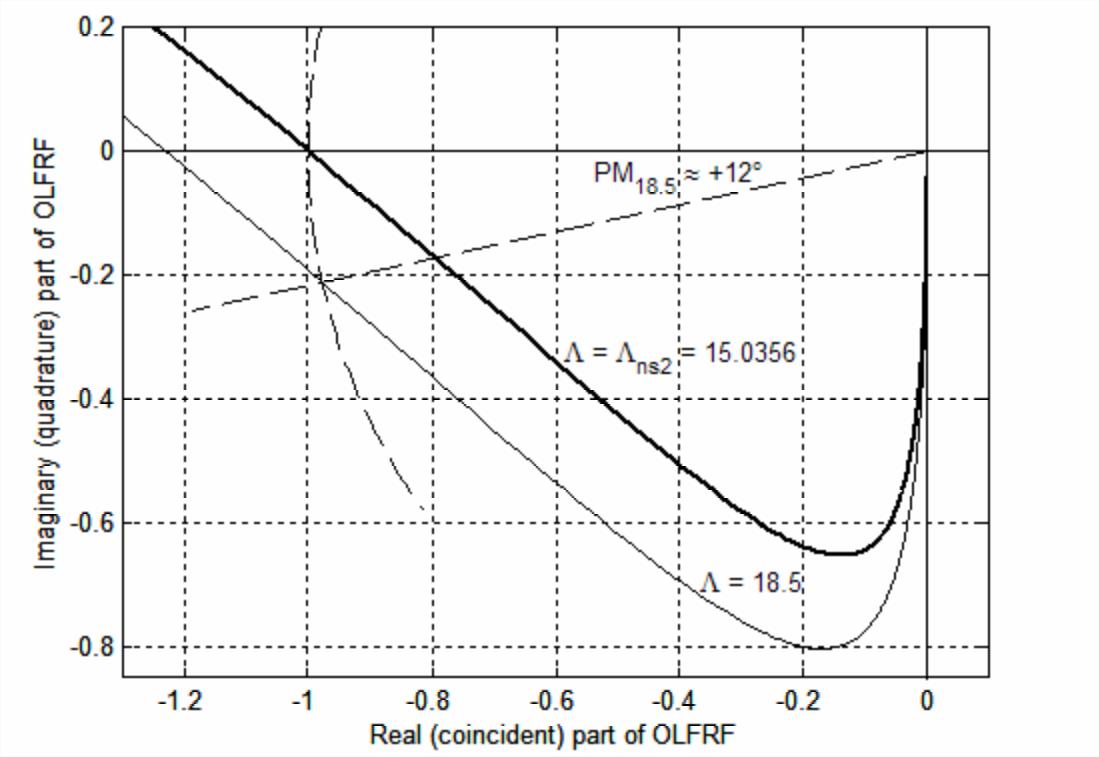
Para ganar\(\Lambda = 18.5\), hay dos cruces de fase: uno evidente en la Figura\(\PageIndex{6}\) en\(-18.5 / 15.0356+j 0=-1.230+j 0\), y el otro más allá del rango de Figura\(\PageIndex{6}\) en\(-18.5 / 0.96438+j 0=-19.18+j 0\). Sabemos por Figura\(\PageIndex{3}\) que el sistema de bucle cerrado con\(\Lambda = 18.5\) es estable, aunque débilmente. Sin embargo, el margen de ganancia calculado a partir de cualquiera de los dos cruces de fase sugiere inestabilidad, mostrando que ambos son métricas de estabilidad engañosamente defectuosas. Por otro lado, el margen de fase mostrado en la Figura\(\PageIndex{6}\),\(\mathrm{PM}_{18.5} \approx+12^{\circ}\), indica correctamente una estabilidad débil.

Sacamos las siguientes conclusiones de las discusiones anteriores de Figuras\(\PageIndex{3}\) a través de\(\PageIndex{6}\), relativas a un sistema “poco común” con una función de transferencia de bucle abierto como Ecuación\(\ref{eqn:17.18}\):

1. el margen de ganancia como se define en la Figura\(\PageIndex{5}\) puede ser una métrica ambigua, poco confiable e incluso engañosa de estabilidad de bucle cerrado;
2. el margen de fase como se define en la Figura\(\PageIndex{5}\), por otro lado, suele ser una métrica inequívoca y confiable, con\(\mathrm{PM}>0\) indicación de estabilidad de bucle cerrado e\(\mathrm{PM}<0\) indicando inestabilidad de bucle cerrado.

Conclusión 2. respecto al margen de fase es una forma del criterio de estabilidad Nyquist, una forma que es pertinente para sistemas como el de Ecuación\(\ref{eqn:17.18}\); no es la forma más general del criterio, pero es suficiente para el alcance de este libro de texto introductorio.

Las pruebas del criterio general de estabilidad Nyquist se basan en la teoría de funciones complejas de una variable compleja; muchos libros de texto sobre teoría de control presentan tales pruebas, siendo una de las más claras la de Franklin, et al. , 1991, páginas 261-280. Esta referencia muestra que el criterio de forma de estabilidad descrito anteriormente [Conclusión 2.] no es lo suficientemente general para manejar todos los casos que puedan surgir. Por ejemplo, el caso inusual de un sistema de bucle abierto que tiene polos inestables requiere el criterio general de estabilidad Nyquist. Sin embargo, el hardware real de dicho sistema de bucle abierto no pudo ser sometido a pruebas experimentales de frecuencia-respuesta debido a su carácter inestable, por lo que un ingeniero de sistemas de control encontraría necesario analizar un modelo matemático del sistema. Es probable que el análisis teórico más confiable de dicho modelo para la estabilidad de bucle cerrado sea mediante el cálculo de loci de raíces en bucle cerrado, no por el cálculo de la respuesta de frecuencia de bucle abierto. Otro caso inusual que requeriría el criterio general de estabilidad Nyquist es un sistema de bucle abierto con más de un cruce de ganancia, es decir, un sistema cuya curva de respuesta de frecuencia cruza más de una vez el círculo unitario que se muestra en la Figura\(\PageIndex{2}\), haciendo ambigua la definición de margen de fase.

Concluimos este capítulo sobre criterios de estabilidad de frecuencia-respuesta observando que los márgenes de ganancia y fase se utilizan también como objetivos de diseño de ingeniería. Por ejemplo, Brogan, 1974, página 25, escribió “La experiencia ha demostrado que la respuesta transitoria aceptable generalmente requerirá márgenes de estabilidad del orden de\(\mathrm{PM}>30^{\circ}\),\(\mathrm{GM}>6\) dB”. Franklin, et al. , 1991, página 285, escribió “Muchos ingenieros piensan directamente en términos de\(\text { PM }\) juzgar si un sistema de control está adecuadamente estabilizado. De\(\text { PM }\) esta manera, a menudo se considera que un margen de fase de 30° es el más bajo aceptable\(\text { PM }\), con valores por encima de 30° deseables”.

¹ Esta función de transferencia fue inventada con fines de demostración. No representa ningún sistema físico real específico, pero tiene características que son representativas de algunos sistemas reales. \(\Lambda\)La ganancia tiene unidades físicas de s ^-1, pero no nos molestaremos en mostrar unidades en la siguiente discusión.