1.9: Elementos de circuito inductivo y capacitivo

Hasta el momento, hemos tratado con elementos de circuito que no tienen memoria y que, por lo tanto, se caracterizan por un comportamiento instantáneo. Las expresiones que se utilizan para calcular lo que están haciendo estos elementos son algebraicas (y para la mayoría de los elementos también son lineales). Resulta que gran parte de los circuitos que vamos a estudiar pueden ser tan caracterizados, con parámetros complejos.

Sin embargo, tomamos una desviación rápida para discutir brevemente el comportamiento transitorio de los circuitos que contienen condensadores e inductores.

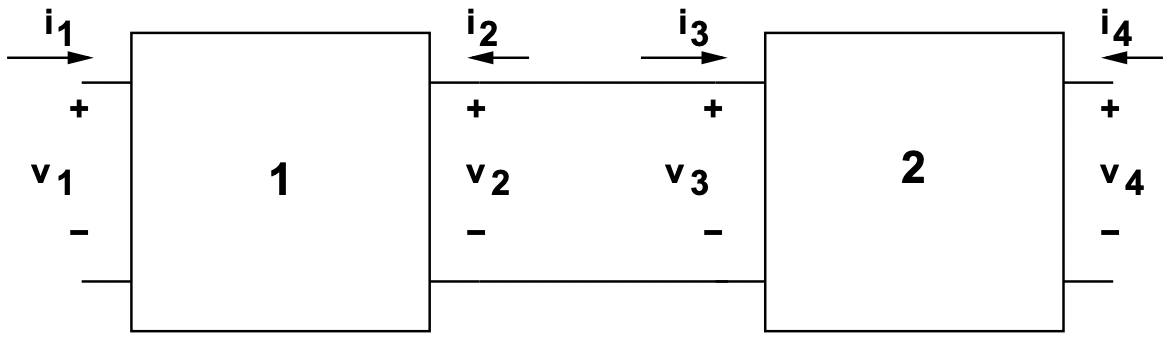Figura 24: Cascada de redes de dos puertos

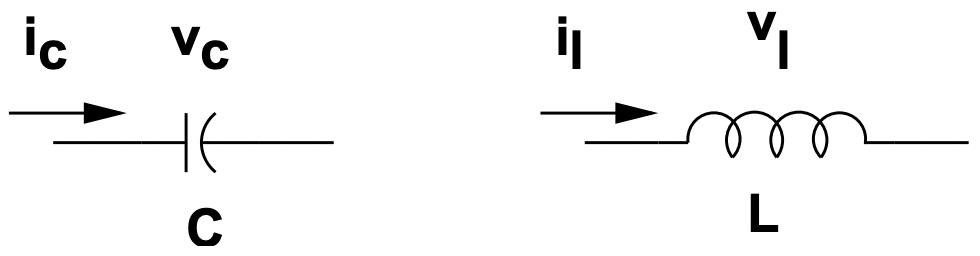Figura 25: Capacitancia e inductancia

Los símbolos para elementos de circuito capacitivo e inductivo se muestran en la Figura 25. Se caracterizan por las relaciones entre voltaje y corriente:

\[\ i_{c}=C \frac{d v_{c}}{d t} \quad\quad\quad v_{\ell}=L \frac{d i_{\ell}}{d t}\label{18} \]

Obsérvese que, si bien estos elementos son lineales, dado que las derivadas del tiempo están involucradas en su caracterización, las expresiones que describen su comportamiento en las redes se convertirán en ecuaciones

Caso Simple: R-C

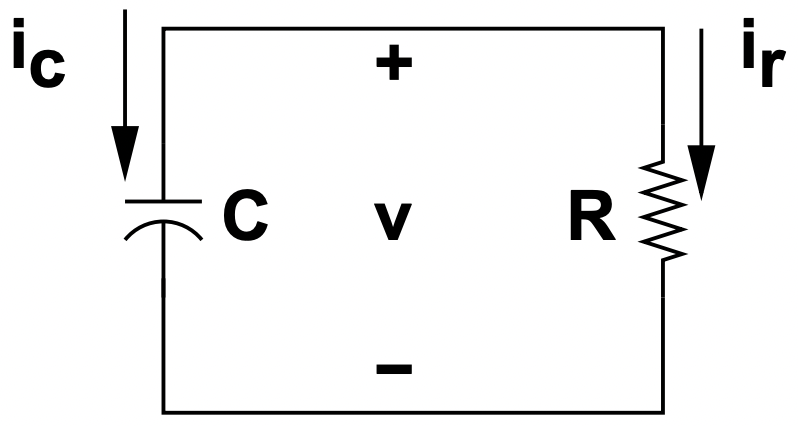Figura 26: Caso simple: R-C

La figura 26 muestra una conexión simple de una resistencia y una capacitancia. Este circuito tiene sólo dos nodos, por lo que hay una sola tensión v a través de ambos elementos. Los dos elementos producen las restricciones:

\ (\\ comenzar {alineado}
i_ {r} &=\ frac {v} {R}\\
i_ {c} &=\ frac {d v} {d t}
\ final {alineado}\)

y, puesto que\(\ i_{r}=-i_{c}\),

\(\ \frac{d v}{d t}+\frac{1}{R C} v=0\)

Ahora bien, sabemos que este tipo de ecuación lineal de primer orden se resuelve mediante:

\(\ v \sim e^{-\frac{t}{R C}}\)

(Para confirmar esto, simplemente sustituya el exponencial en la ecuación diferencial). Entonces, si tenemos alguna condición inicial, digamos\(\ v(t=0)=V_{0}\), entonces

\(\ v=V_{0} e^{-\frac{t}{R C}}\)

Este fue un caso trivial, ya que no describimos cómo pudo haber ocurrido esa condición inicial. Pero consideremos un problema estrechamente relacionado, ilustrado en la Figura 27.

Estuche simple con unidad

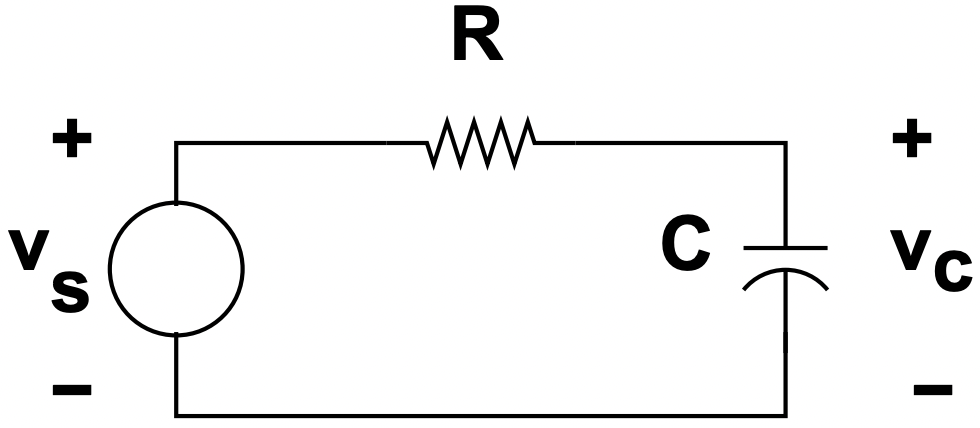Figura 27: Circuito RC con Accionamiento

El análisis de este circuito se logra señalando que contiene un solo bucle, y sumando los voltajes alrededor del bucle encontramos:

\(\ R C \frac{d v_{c}}{d t}+v_{c}=v_{s}\)

Ahora, supongamos que la fuente de voltaje es un paso:

\(\ v_{s}=V_{s} u_{-1}(t)\)

Deberíamos definir la función de paso con cierto cuidado, ya que es de bastante utilidad. El paso es uno de una jerarquía de funciones de singularidad. Se define como:

\ [\ u_ {-1} (t) =\ left\ {\ begin {array} {ll}
0 & t<0\\
1 & t>0
\ end {array}\ right. \ label {19}\]

Ahora bien, recordando que las ecuaciones diferenciales tienen soluciones particulares y homogéneas, y que para\(\ t>0\) una solución particular que resuelve la ecuación diferencial es:

\(\ v_{c p}=V\)

Por supuesto esto no satisface la condición inicial que es que la capacitancia sea descargada:\(\ v_{c}(t=0+)=0\). Nuevamente, recuerde que toda la solución es la suma de la solución particular y una homogénea, y que la solución homogénea es el caso no impulsado. Para satisfacer la condición inicial, la solución homogénea debe ser:

\(\ c_{c h}=-V e^{-\frac{t}{R C}}\)

Para que la solución total sea simplemente:

\(\ v_{c}=V\left(1-e^{-\frac{t}{R C}}\right)\)

A continuación, supongamos\(\ v_{s}=u_{-1}(t) V \cos \omega t\). Sabemos que la solución homogénea debe ser de la misma forma, pero la solución particular es un poco más complicada. En capítulos posteriores aprenderemos a facilitar el proceso de extracción de la solución particular, pero por el momento, supongamos que con una unidad sinusoidal obtendremos una respuesta sinusoidal de la misma frecuencia. Así adivinaremos

\(\ v_{c p}=V_{c p} \cos (\omega t-\phi)\)

La derivada del tiempo es

\(\ \frac{d v_{c p}}{d t}=\omega V_{c p} \sin (\omega t-\phi)\)

para que podamos encontrar una ecuación algebraica para la solución particular:

\(\ V \cos \omega t=V_{c p}(\cos (\omega t-\phi)+\omega R C \sin (\omega t-\phi))\)

Tenga en cuenta las identidades trigonométricas:

\ (\\ comenzar {alineado}
\ cos (\ omega t-\ phi) &=\ cos\ phi\ cos\ omega t+\ sin\ phi\ sin\ omega t\
\ sin (\ omega t-\ phi) &=-\ sin\ phi\ cos\ omega t+\ cos\ phi\ sin\ omega t
\ fin {alineado}\)

Dado que los términos seno y coseno son ortogonales, podemos equiparar coeficientes de seno y coseno para obtener:

\ (\\ comenzar {alineado}
V &=V_ {c p} [\ cos\ phi+\ omega R C\ sin\ phi]\\
0 &=V_ {c p} [\ sin\ phi+\ omega R C\ cos\ phi]
\ end {alineado}\)

El segundo de estos se puede resolver para el ángulo de fase:

\(\ \phi=\tan ^{-1} \omega R C\)

y la cuadratura de ambas ecuaciones y la adición de:

\(\ V^{2}=V_{c p}^{2}\left(1+(\omega R C)^{2}\right)\)

para que la solución particular sea:

\(\ v_{c p}=\frac{V}{\sqrt{1+(\omega R C)^{2}}} \cos (\omega t-\phi)\)

Por último, si el condensador está inicialmente descargado\(\ \left(v_{c}(t=0+)=0\right)\), podemos agregar en la solución homogénea (ya conocemos la forma de esto), y encontrar la solución total para ser:

\(\ v_{c} p=\frac{V}{\sqrt{1+(\omega R C)^{2}}}\left[\cos (\omega t-\phi)-\cos \phi e^{-\frac{t}{R C}}\right]\)

Esto se muestra en la Figura 28

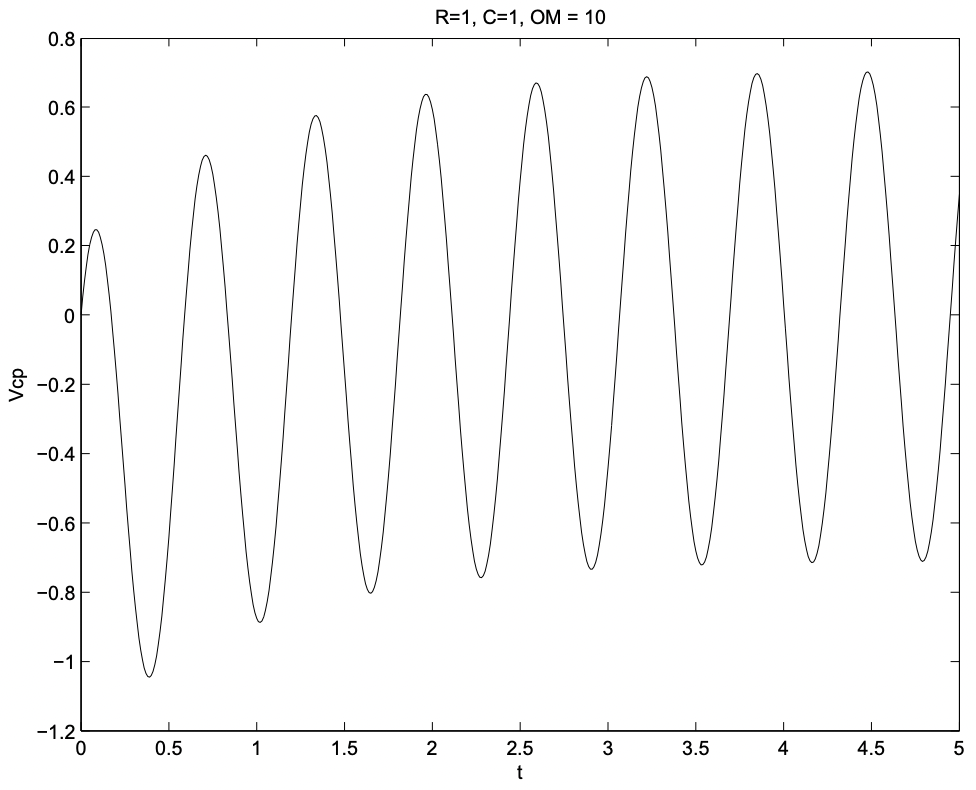Figura 28: Ejemplo de voltaje de salida para RC

Ejemplo de sistema de segundo orden

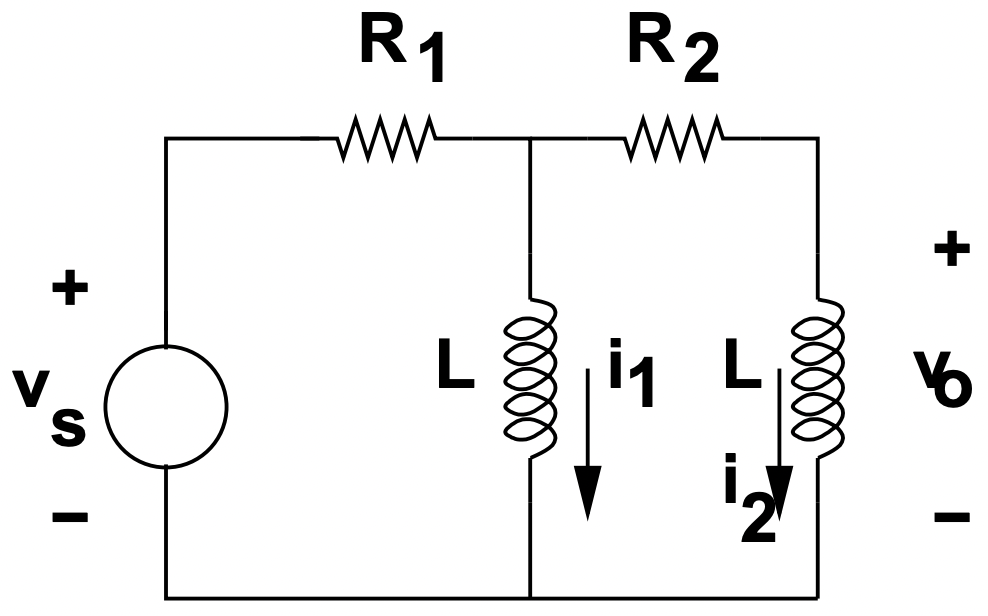Figura 29: Circuito de dos inductores

La Figura 29 muestra una red con dos inductancias y dos resistencias. Supongamos que esto es impulsado por un paso de voltaje:\(\ v_{s}=V_{s} u_{-1}(t)\). Tenga en cuenta que, con dos inductancias, requeriremos dos condiciones iniciales para completar la solución.

La solución de estado estacionario (particular) es\(\ v_{o}=0\). Por supuesto, habrá corriente fluyendo en cada una de las inductancias, pero si la excitación es constante no habrá derivada temporal de la corriente de manera que el voltaje a través de cada una de las inductancias eventualmente caerá a cero.

Las condiciones iniciales se pueden encontrar por inspección. Justo después\(\ t=0\) (tenga en cuenta que usamos\(\ t=0+\) para esto), el voltaje de salida debe ser:

\(\ v_{o}(t=0+)=V_{s}\)

Esto debe ser así ya que no se puede hacer que la corriente fluya instantáneamente en ninguna de las inductancia, de manera que no haya corriente en ninguna de las resistencias.

La segunda condición inicial es la tasa de cambio de voltaje justo después del instante del paso de voltaje. Para encontrar esto, tenga en cuenta que el voltaje de salida es igual al voltaje de la fuente menos las caídas de voltaje a través de cada una de las dos resistencias.

\(\ v_{o}=v_{s}-R_{2} i_{2}-R_{1}\left(i_{1}+i_{2}\right)\)

Si diferenciamos esto con respecto al tiempo y observamos que la derivada de tiempo de una constante (después del paso la tensión de entrada es constante) es cero:

\(\ \frac{d v_{o}}{d t}(t=0+)=-\left(R_{1}+R_{2}\right) \frac{d i_{2}}{d t}-R_{1} \frac{d i_{1}}{d t}\)

Ahora, ya que justo después del instante del paso ambas inductancias tienen el voltaje de fuente\(\ V_{s}\) a través de ellas:

\(\ \left.\frac{d i_{1}}{d t}\right|_{t=0+}=\left.\frac{d i_{2}}{d t}\right|_{t=0+}=\frac{V_{s}}{L}\)

la tasa de cambio de voltaje en\(\ t=0+\) es:

\(\ \left.\frac{d v_{o}}{d t}\right|_{t=0+}=-\frac{2 R_{1}+R_{2}}{L} V_{s}\)

Ahora, podemos encontrar la solución homogénea usando el método loop. Estableciendo la fuente a cero, asuma una corriente\(\ i_{a}\) en el bucle izquierdo y\(\ i_{b}\) en el bucle de la derecha. KVL alrededor de estos dos bucles rinde:

\ (\\ begin {array} {c}
R_ {1} i_ {a} +L\ frac {d} {d t}\ left (i_ {a} -i_ {b}\ right) =0\\
R_ {2} i_ {b} +2 L\ frac {d i_ {b}} {d t} -L\ frac {i_ {a} {d t} =0
\ end {array}\)

Con un poco de manipulación, estos se convierten en:

\ (\\ begin {array} {c}
L\ frac {d i_ {a}} {d t} +2 R_ {1} i_ {a} +R_ {2} i_ {b} =0\\
L\ frac {d i_ {b}} {d t} +R_ {1} i_ {a} +R_ {2} i_ {b} =0
\ fin {matriz}\)

Supongamos que las soluciones son de la forma\(\ I e^{s t}\), y este conjunto de ecuaciones simultáneas se convierte en:

\ (\\ izquierda [\ begin {array} {cc}
\ izquierda (s L+2 R_ {1}\ derecha) & R_ {2}\\
R_ {1} &\ izquierda (s L+R_ {2}\ derecha)
\ end {array}\ derecha]\ left [\ begin {array} {c}
I_ {a}\
I_ {b}
\ end {array}\ right] =\ left [\ begin {array} {l}
0\\
0
\ end {array}\ derecha]\)

Necesitamos resolver esto para s (para encontrar valores de s para los cuales este conjunto es verdadero, y esa es simplemente la solución de la “ecuación característica”

\(\ \left(s L+2 R_{1}\right)\left(s L+R_{2}\right)-R_{1} R_{2}=0\)

que es lo mismo que:

\(\ s^{2}+\frac{2 R_{1}+R_{2}}{L} s+\frac{R_{1}}{L} \frac{R_{2}}{L}=0\)

Ahora bien, por el bien de los “buenos números”, supongamos que R1 = 2R, R2 = 3R. La ecuación característica es:

\(\ s^{2}+7 \frac{R}{L} s+6\left(\frac{R}{L}\right)^{2}=0\)

que factores muy bien en\(\ \left(s+\frac{R}{L}\right)\left(s+6 \frac{R}{L}\right)=0\\), o los dos valores de s son\(\ s=-\frac{R}{L}\) y\(\ s=-6 \frac{R}{L}\).

Dado que la solución particular a ésta es cero, tenemos una solución total que es:

\(\ v_{o}=A e^{-\frac{R}{L} t}+B e^{-6 \frac{R}{L} t}\)

Las condiciones iniciales son:

\ (\\ comenzar {alineado}
\ izquierda.v_ {o}\ derecha|_ {t=0+} =A+B &=V_ {s}\\
\ izquierda. \ frac {d v_ {o}} {d t}\ derecha|_ {t=0+} =-\ frac {R} {L} (A+6 B) &=-7\ frac {R} {L} V_ {s}
\ end {alineado}\)

La solución a ese par de expresiones es:

\(\ A=-\frac{V_{s}}{5} \quad\quad B=\frac{6 V_{s}}{5}\)

y esto se muestra en la Figura 30.

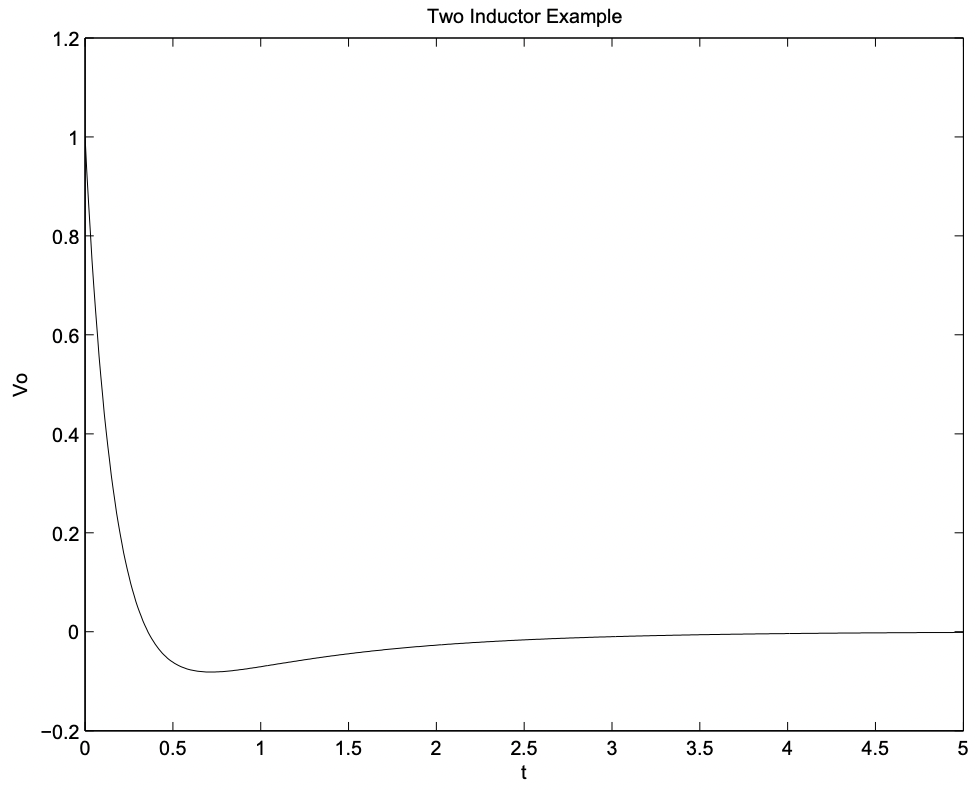Figura 30: Ejemplo de voltaje de salida para dos inductores